Вопрос 38. Максимизация выпуска и спрос на ресурсы.

Пусть нам дана конкретная технология производства продукта:

Q=K L

а также мы имеем стоимостное ограничение на ресурсы:

C=rK+wL,

где r – арендная плата за оборудование, а w – ставка заработной платы. Тогда данная задача формулируется так:

(максимизация выпуска)

( при заданном ограничении) Т.к. это задача на условный экстремум (есть целевая функция, есть уравнение ограничения), то можно выписать функцию Лагранжа:

F(K,L, )= K L + (C-rK-wL)

Выпишем условия первого порядка:

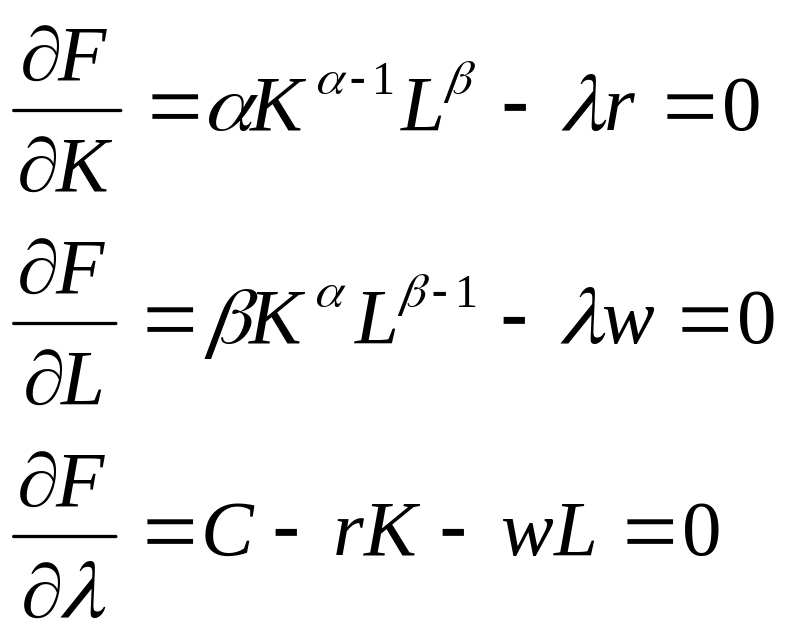
Имеем систему из трех уравнений с тремя неизвестными. Для удобства решения разделим первое уравнение на второе.

Из этой системы находим K и L, т.е. в данном случае такую конфигурацию ресурсов, при которой достигается максимальный выпуск.

K=

L=

Q=( ) ( ) =

K и L есть в данном случае функции спроса на ресурсы, зависящие от C, r, и w. Величина Q есть в данном случае максимальный выпуск, которого достигает фирма в точке (K,L)=( , ). Q есть функция условного предложения фирмы.

Вопрос 39. Предложение конкурентной фирмы в коротком и длительном периодах. Квазипостоянные издержки.

Применим факты, выясненные нами в отношении кривых издержек, для того чтобы вычислить кривую предложения конкурентной фирмы. По определению, конкурентная фирма игнорирует свое влияние на рыночную цену. Таким образом, задачу максимизации, стоящую перед конкурентной фирмой, можно записать:

max py — c(y).

Это говорит просто о том, что конкурентная фирма хочет максимизировать свою прибыль: разность между общим доходом py и издержками c(y).

Какой объем выпуска решит производить конкурентная фирма? Ответ: она будет действовать в точке, где предельный доход равен предельным издержкам, — там, где добавочный доход, приносимый еще одной единицей выпуска, как раз равен добавочным издержкам производства еще одной единицы выпуска. Если бы данное условие не удовлетворялось, фирма всегда могла бы увеличить свою прибыль путем изменения своего объема выпуска.

В случае конкурентной фирмы предельный доход есть просто цена. Чтобы увидеть это, спросим себя, сколько добавочного дохода получит конкурентная фирма, увеличив выпуск на Dy. Мы получим

DR = pDy,

поскольку согласно нашей гипотезе p не изменяется. Поэтому добавочный доход на единицу выпуска задается формулой

DR/Dy = p,

представляющей собой выражение для предельного дохода.

Таким образом, конкурентная фирма выберет объем выпуска y в точке, где предельные издержки как раз равны рыночной цене. В условных обозначениях:

p = MC(y).

Мы хотим найти объем выпуска, максимизирующий прибыль при данной рыночной цене p. Если при каком-то объеме выпуска y цена больше предельных издержек, фирма может увеличить свою прибыль, чуть увеличив выпуск. Ведь превышение ценой предельных издержек означает, что

p — .

Поэтому увеличение выпуска на Dy означает, что

pDy — .

Упростив это неравенство, мы находим, что

pDy —Dc > 0,

а это означает, что прирост общего дохода от добавочного выпуска превышает прирост издержек. Следовательно, прибыль при этом должна увеличиться.

Аналогичные рассуждения можно провести и для случая, когда цена ниже предельных издержек. Тогда сокращение выпуска приведет к увеличению прибыли, поскольку потерянный при этом доход более, чем компенсируется сократившимися издержками.

Таким образом, при оптимальном объеме выпуска фирма должна производить в точке, где цена равна предельным издержкам. Каков бы ни был уровень рыночной цены p, фирма выберет объем выпуска y, соответствующий условию p = MC(y). Поэтому кривая предельных издержек конкурентной фирмы есть в точности ее кривая предложения. Или, другими словами, рыночная цена есть в точности предельные издержки до тех пор, пока каждая фирма производит объем выпуска, максимизирующий ее прибыль.

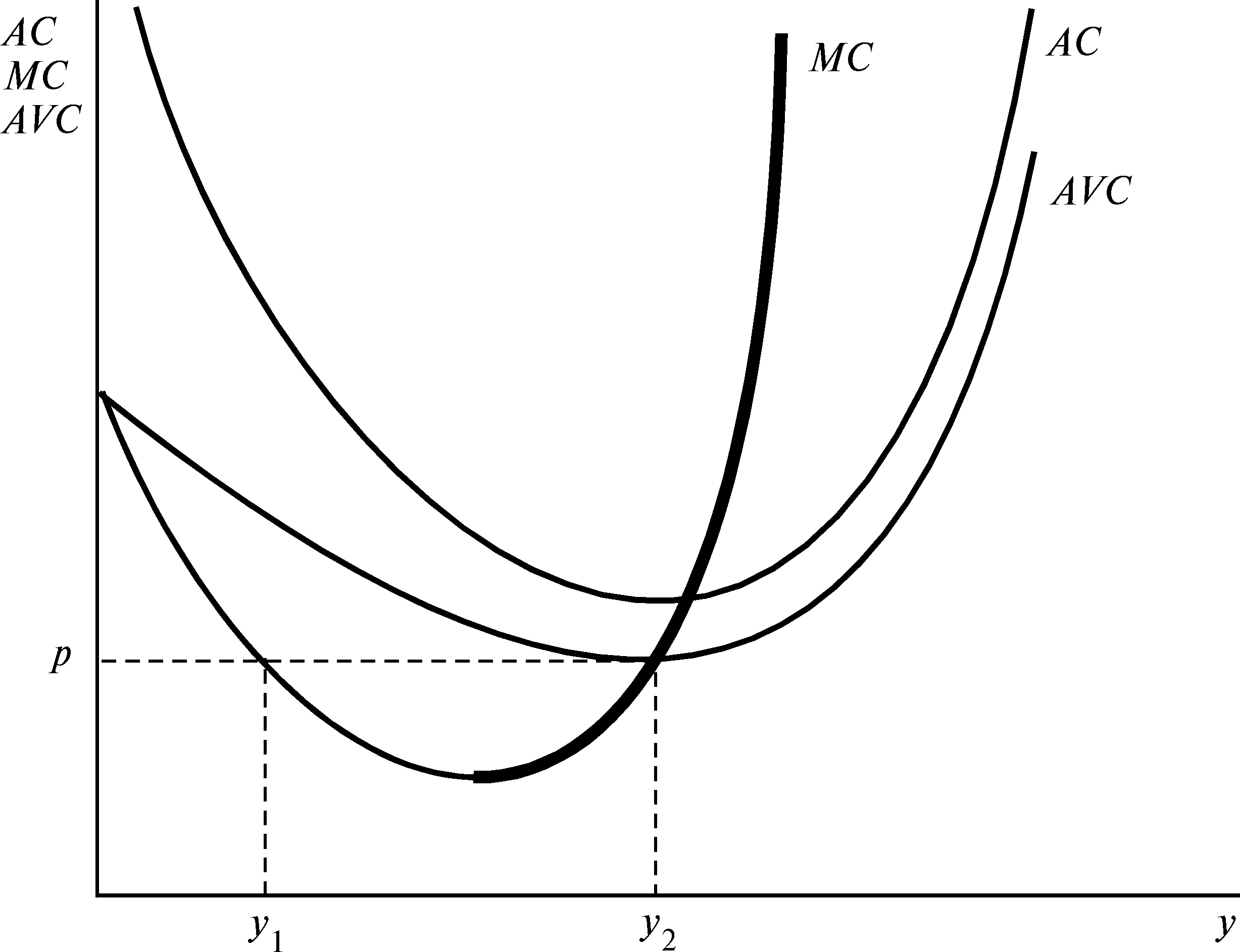
Рисунок 21.2 Предельные издержки и предложение.

В данных рассуждениях предполагается, что выгодно производить что-то. Но в конце концов самым выгодным для фирмы могло бы оказаться и производство нулевого выпуска. Поскольку всегда имеется возможность произвести нулевой объем выпуска, мы должны сравнить точку предполагаемой максимизации прибыли с точкой нулевого производства.

Если фирма производит нулевой выпуск, она по-прежнему должна оплачивать постоянные издержки F. Следовательно, прибыль от производства нуля единиц выпуска равна просто —F. Прибыль от производства объема выпуска y есть py — c_v(y) — F. Фирме выгоднее прекратить деятельность, когда

—F > py —c_v(y) —F,

т.е. когда "прибыль" от нулевого производства и просто оплаты постоянных издержек превышает прибыль от производства в точке, где цена равна предельным издержкам. Преобразование этого неравенства дает нам условие закрытия:

Если средние переменные издержки больше p, фирме выгоднее производить ноль единиц выпуска. В этом есть смысл, поскольку это условие говорит о том, что общий доход от продажи выпуска y не покрывает даже переменных издержек производства c_v(y). В этом случае фирме лучше выйти из бизнеса. Если она не будет производить ничего, она потеряет постоянные издержки, но она потеряла бы даже больше, если бы продолжала производить.

Эти рассуждения показывают, что только те части кривой предельных издержек, которые лежат над кривой средних переменных издержек, могут состоять из точек, принадлежащих кривой предложения. Если точка, в которой цена равна предельным издержкам, находится под кривой средних переменных издержек, то в оптимуме фирма предпочтет производить нуль единиц выпуска.

Теперь перед нами вырисовывается картина кривой предложения, подобная изображенной на рис.21.3. Конкурентная фирма производит в той части кривой предельных издержек, которая является восходящей и лежит над кривой средних переменных издержек.

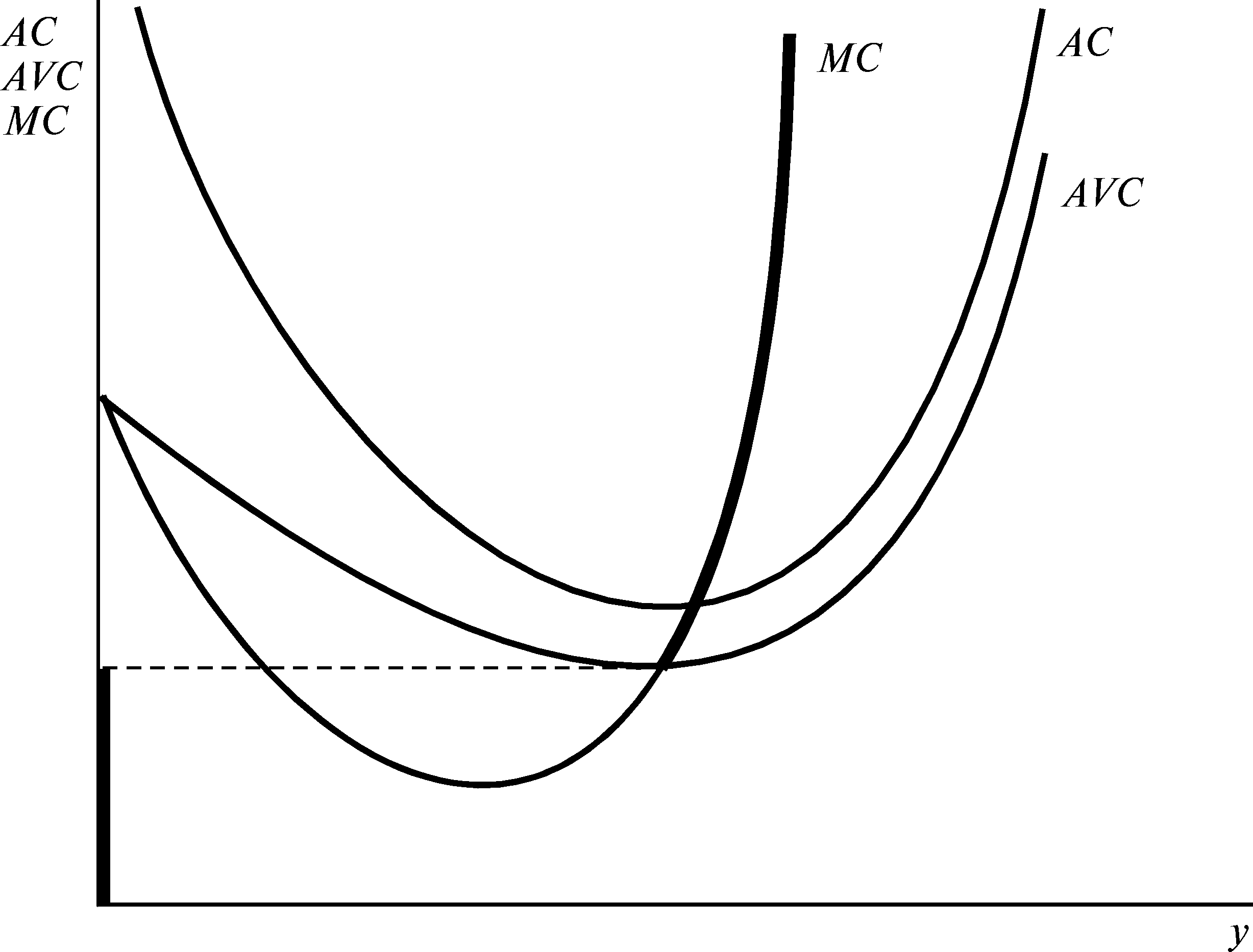
Рисунок 21.3 Средние переменные издержки и предложение.

Кривая долгосрочного предложения конкурентной фирмы строится на основании тех же принципов, что и кривая ее краткосрочного предложения. Поскольку по условию оптимальности P=MC , кривая предложения в долгосрочном периоде совпадает с кривой долгосрочных предельных издержек. Но в долгосрочном периоде все издержки фирмы являются переменными. Если цена становится ниже минимальных средних издержек, то фирма может избавиться от убытков, просто прекратив выпуск. Поэтому кривая долгосрочного предложения фирмы совпадает с кривой долгосрочных предельных издержек только на участке, лежащем не ниже минимума средних издержек, при P>=minAC. Квазипостоянные издержки — это издержки, которые тоже не зависят от объема выпуска, но должны оплачиваться только при условии производства фирмой положительного объема выпуска.

В длительном периоде по определению постоянных издержек не бывает, однако вполне могут существовать квазипостоянные издержки. Если началу производства какого-то объема выпуска должна предшествовать затрата какой-то постоянной суммы, то можно говорить о наличии квазипостоянных издержек.