1. Конечный предел числовой последовательности. Необходимое условие его существования. Формулировка критерия Коши сходимости числовой последовательности.

Последовательность – функция многочисленного аргумента, закон, где каждому числу соответствует значение некоторого числа.

Предел последовательности:

Критерий Коши:

Ч исловая последовательность сходится тогда и только тогда, когда для любого ε > 0 существует номер N такой, что при всех n > N(ε)  и любых натуральных m выполняется неравенство 

2. Критерий сходимости монотонной последовательности.

Теорема: Монотонная ограниченная последовательность имеет предел.

Д оказательство: Докажем теорему для монотонной возрастающей последовательности  . Докажем, что точная верхняя граница для последовательности   и будет ее пределом. Действительно, по определению точной верхней границы

К роме того, какое бы ни взять число  , найдется такой номер  , что

Т ак как последовательность монотонна, то при   будет  , а значит, и   и выполняются неравенства

откуда и следует, что

3. Бесконечно малые последовательности и их свойства. Бесконечно большие последовательности и их связь с бесконечно малыми последовательностями.

Бесконечно малые последовательности: Последовательность называется бесконечно малой, если . Например, последовательность чисел — бесконечно малая.

Функция называется бесконечно малой в окрестности точки  , если  .

Функция называется бесконечно малой на бесконечности, если   либо  .

Также бесконечно малой является функция, представляющая собой разность функции и её предела, то есть если  , то  ,  Свойства бесконечно малых:

• Сумма конечного числа бесконечно малых — бесконечно малая.

• Произведение бесконечно малых — бесконечно малая.

• Произведение бесконечно малой последовательности на ограниченную — бесконечно малая. Как следствие, произведение бесконечно малой на константу — бесконечно малая.

• Если   — бесконечно малая последовательность, сохраняющая знак, то   — бесконечно большая последовательность.

Бесконечно большая величина:

Последовательность   называется бесконечно большой, если  .

Функция называется бесконечно большой в окрестности точки  , если  .

Функция называется бесконечно большой на бесконечности, если   либо  .

Связь между ними:  

Т еорема 1. Если { х_n} — бесконечно большая последовательность и все ее члены отличны от нуля, то последовательность

бесконечно малая, и, обратно, если {α_n} — бесконечно малая последовательность и все её члены отличны от нуля {α_n} ≠ 0, то последовательность { 1 / α_n } – бесконечно большая.   Доказательство. Пусть { х_n} — бесконечно большая последовательность. Возьмем любое как угодно малое положительное число ε > 0 и положим

С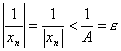 огласно определению для этого существует такой номер N , что при n > N будет | x_n | > A. Отсюда получаем, что

для всех n > N. А это значит, что последовательность бесконечно малая.

4. Теорема о пределах суммы, произведения, частного сходящейся последовательности.

Т еорема 1. Предел алгебраической суммы двух, трех и вообще определенного числа функций равен алгебраической сумме пределов этих функций, т.е.

.Доказательство. Проведем доказательство для двух слагаемых, так как для любого числа слагаемых оно проводится так же. Пусть  .Тогда f(x)=b+α(x) иg(x)=c+β(x),

г де α и β – бесконечно малые функции. Следовательно, f(x) + g(x)=(b + c) + (α(x) + β(x)).Так как b + cесть постоянная величина, а α(x) + β(x) – функция бесконечно малая, то

Т еорема 2. Предел произведения двух, трех и вообще конечного числа функций равен

произведению пределов этих функций:

.Доказательство. Пусть  . Следовательно, f(x)=b+α(x) и g(x)=c+β(x) и fg = = (b + α)(c + β) = bc + (bβ + cα + αβ).

П роизведение bc есть величина постоянная. Функция bβ + c α + αβ на основании свойств бесконечно малых функций есть величина бесконечно малая.

Поэтому .

Следствие 1. Постоянный множитель можно выносить за знак предела:

.

Следствие 2. Предел степени равен степени предела:

.

Теорема 3. Предел частного двух функций равен частному пределов этих функций, если предел знаменателя отличен от нуля, т.е.

.

Доказательство. Пусть  . Следовательно, f(x)=b+α(x) и g(x)=c+β(x), где α, β – бесконечно малые. Рассмотрим частное

.

Дробь  является бесконечно малой функцией, так как числитель есть бесконечно малая функция, а знаменатель имеет предел c²≠0.

5. Теоремы о пределах последовательностей, связанных неравенствами.

1) Если последовательности { },{ } и { } таковы, что   для всех ,  = =a, то последовательность { } сходится и  =a

Д:

По определению предела  :

Отсюда,  , где N=max( ), выполняется условие  . Значит

2) Если   , , причем a<b, то  .

Д:

Выберем  >0 так, чтобы  -окрестности точек a и b не пересекались. Возьмем  =(b-a)/3>0. Согласно определению предела по заданному   можно найти номера   и  такие, что   при всех   и   при всех   . Пусть  =max( , ). Тогда при всех  :  .

6. Число е, как предел последовательности с общим членом a(n)=(1+1/n)^n

Последовательность с общим членом     имеет конечный предел при   .  Замечание. Для обозначения этого предела используется символ e:

Число  e  является иррациональным, приближенное значение которого равно

e = 2.71828182845904523536028747135266249775724709…

Доказательство. Покажем сначала, что     представляет собой монотонно возрастающую последовательность. Согласно биному Ньютона,

 

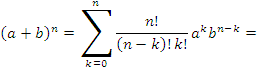
Полагая   , получим

 

А налогично,

 

Сравним выражения для     и   . 

В о-первых, оба эти выражения содержат только положительные слагаемые.  Во-вторых, начиная со второго слагаемого, каждый член в выражении для     превышает соответствующий член выражения для   , поскольку

В-третьих, выражение для     состоит из большего числа слагаемых. Следовательно,    

Д алее докажем, что последовательность     является ограниченной. Действительно, первый член любой монотонно возрастающей последовательности является ее наибольшей нижней границей и, таким образом,     для всех натуральных значений  n.  Перейдем к доказательству существования верхней границы. Очевидно, что

 

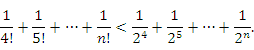
Кроме того,     для всех  k > 3. Тогда

Правая часть этого неравенства представляет собой сумму членов убывающей геометрической прогрессии. В качестве верхней границы этой суммы выступает любое число   . Таким образом, последовательность с общим членом

представляет собой ограниченную монотонно возрастающую последовательность и, следовательно, имеет конечный предел – согласно теореме о монотонных последовательностях.

7. Конечный предел функции действительного переменного (по Коши и по Гейне) при x→a(a – число или ∞). Бесконечно большие функции при x→a. Односторонние пределы.