
- •4/ Основные теоремы о дифференцировании функций
- •5 Производные основных элементарных функций
- •9 Приближенные вычисления при помощи дифференциала
- •11 Необходимые и достаточные условия монотонности
- •12 Необходимые и достаточные условия экстремума
- •13 Нахождение наибольшего и наименьшего значения функции на отрезке
- •14 Выпуклость кривой, точки перегиба (определение; необходимые, достаточные условия).
- •15 Асимптоты графика функции. Нахождение наклонных асимптот
- •16 Суммарные, средние и предельные показатели, связь между ними.
- •18 Приложения производной в экономической теории
- •19 Формула Тейлора. Остаточный член в форме Лагранжа.
- •20 Разложение элементарных функций по формуле Тейлора.
1
Производной функции ![]() в
точке x0 в
обозначении
в
точке x0 в
обозначении ![]() называется
предел отношения приращения функции к
приращению аргумента, когда приращение
аргумента стремится к нулю, т. е.
называется
предел отношения приращения функции к
приращению аргумента, когда приращение
аргумента стремится к нулю, т. е.
 .
.
Производные элементарных функций представлены в табл. 1.
Таблица 1
1.
2.
3.
4.
5.
|
6.
7.
8. 9. |
10.
11.
12.
13.
|
функции
.
Точка M0 на
графике имеет координаты (x0, ![]() ).
Прямая M0M является
касательной для линии
и
наклонена к оси Ox под
углом
).
Прямая M0M является
касательной для линии
и
наклонена к оси Ox под
углом ![]() .
.
Геометрическое истолкование производной состоит в том, что угловой коэффициент касательной к графику функции в точке с абсциссой x0 равен производной этой функции в точке x0:
![]() (1.1)
(1.1)
Очевидно, что уравнение касательной M0K имеет вид:
![]() (1.2)
(1.2)

экономический
-MC характеризует приближенно дополнительные затраты на производство дополнительной единицы продукции :MC=TC’(Q)
где
MC - предельные издержки (marginal costs);
TC - общие издержки (total costs);
Q – количество
-P (Q) = R (Q) - C (Q)
R(q) - выручка от продаж; C(q) -издержки производства; прибыль П(q)
П'(q) =R'(q) - С'(q)
R(q) = pq; R'(q) = p
Прибыль макс –р= С'(q)
-Относительная скорость изменения (темп) функции y = f(x) определяется ее логарифмической производной
Ty
=
(ln
y)’
=
 .
.
-Эластичность функции y = f(x) предел отношения относительного приращения функции к относительному приращению независимой переменной x при x 0:
Ex(y)
=
 .
.
2 Касательная
Касательная к кривой y = f(x) в точке P(x1,
y1) определяется уравнением :y
= y1 + f'(x1)(x - x1)
нормаль к кривой это прямая Перпендикулярная к касательной проходящая через точку касания (а*а’=-1)
3 Связь
между дифференцируемостью и непрерывностью
Если функция дифференцируема в некоторой точке то она непрерывна в этой точке Таким образом непрерывность функции является необходимым условием ее дифференцируемости
4/ Основные теоремы о дифференцировании функций
Теорема Лагранжа
Если функция f(x) непрерывна на отрезке [а, b] и дифференцируема в интервале (а,b), то существует такая точка с{а,b), что
![]()
Следствие 1. Если производная функции равна нулю в каждой точке некоторого промежутка, то функция есть тождественная постоянная в этом промежутке.
Следствие 2. Если две функции имеют равные производные в некотором промежутке, то они отличаются в этом промежутке лишь постоянным слагаемым.
Корнем (или нулем) функции у = f(x) называется такое значение х = х0 ее аргумента, при котором эта функция обращается в нуль. Геометрически корень функции означает абсциссу точки, в которой график функции пересекает ось их или касается ее.
Теорема Ролля
Между двумя различными корнями дифференцируемой функции содержится по меньшей мере один корень ее производной.
Замечание 1. Теорема имеет простую геометрическую интерпретацию: между значениями а и b имеется по меньшей мере одно значение с такое, что в точке С (с, f(c)) графика функции касательная к графику параллельна оси Ох.
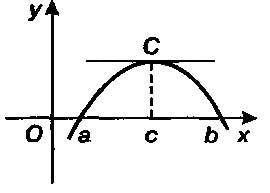
Замечание 2. Теорему можно сформулировать в более общем виде. Если у = f(x) - функция, дифференцируемая на отрезке [а, b] и f(а) = f(b), то между а и b найдется точка с, в которой производная равна нулю, т. е. f'(с) = 0.
Теорема Коши
Если y = f(x) и у = у(х) - две функции, непрерывные на отрезке [а, b] и дифференцируемые в интервале (а, b) причем ф'(x) не равно 0 для любого х(а, b), то между а и b найдется такая точка с, что
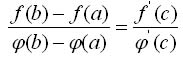
5 Производные основных элементарных функций
1. . 2. . 3. . 4. 5. .
|
6. . 7. . 8. . 9. . |
10. . 11. . 12. . 13. .
|
6 Теорема о производной функции, заданной параметрически
функцииx=φ(t), y
= ψ(t) дифференцируемы
и φ'(t) ≠ 0,
тогда![]()
7 Производные высших порядков
Производной n-го порядка (или n-й производной) называется производная от производной (n-1) порядка:
y(n)=(y(n-1)) .
Производные порядка выше первого называются производными высших порядков.
8 Дифференциалом функции у=ƒ(х) в точке х называется главная часть ее приращения, равная произведению производной функции на приращение аргумента, и обозначается dу (или dƒ(х)):
dy=ƒ'(х)•∆х.
Свойства дифференциала.
Если u = f(x) и v = g(x)- функции, дифференцируемые в точке х, то непосредственно из определения дифференциала следуют следующие свойства:
1) d(u ± v) = (u ± v)¢dx = u¢dx ± v¢dx = du ± dv ; 2) d(uv) = (uv)¢dx = (u¢v + v¢u)dx = vdu + udv
3)
d(Cu) = Cdu ; 4
![]() ; 5)dC=0
;
6)d f(u)=f’(u)du
; 5)dC=0
;
6)d f(u)=f’(u)du
Геометрический смысл дифференциал функции f(x) в точке х равен приращению ординаты касательной к графику этой функции в рассматриваемой точке.
9 Приближенные вычисления при помощи дифференциала
f(x+Δx) ~ f(x)+f’(x)дx ; Δx => 0; Δy ~ dy
10 +Великая Теорема Ферма , - утверждение, что для любого натурального числа n > 2 уравнение xn + yn = zn (уравнение Ферма) не имеет решений в целых ненулевых числах x, y, z.
+маленькая теорема ферма a –Z , p-Простое число
![]()
![]()
![]()
+Правило Лопиталя Условия:
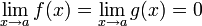 или
или  ;
;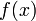 и
и  дифференцируемы
в проколотой окрестности
дифференцируемы
в проколотой окрестности  ;
;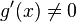 в
проколотой окрестности
;
в
проколотой окрестности
;существует
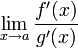 ,
тогда существует
,
тогда существует  .
.


 .
. .
. .
.