Время работы

Докажем, что амортизированное время работы операции   есть  . Поскольку в процедуре нет циклов, ее время работы определяется лишь количеством рекурсивных вызовов каскадного вырезания.

Пусть мы вызвали процедуру каскадного вырезания   раз. Так как реальное время работы операции   без учета рекурсии составляет  , то реальное время работы операции   —  .

Рассмотрим, как изменится потенциал в результате выполнения данной операции. Пусть   — фибоначчиева куча до вызова  . Тогда после   рекурсивных вызовов операции   вершин с пометкой   стало как минимум на   меньше, потому что каждый вызов каскадного вырезания, за исключением последнего, уменьшает количество помеченных вершин на одну, и в результате последнего вызова одну вершину мы можем пометить. В корневом списке прибавилось   новых деревьев (  дерево за счет каскадного вырезания и еще одно из-за самого первого вызова операции  ).

В итоге, изменение потенциала составляет:  . Следовательно, амортизированная стоимость не превышает  . Но поскольку мы можем соответствующим образом масштабировать единицы потенциала, то амортизированная стоимость операции   равна  .

delete

Удаление вершины реализуется через уменьшение ее ключа до   и последующим извлечением минимума. Амортизированное время работы:  .

Поскольку ранее мы показали, что  , то соответствующие оценки доказаны.

Лемма:

Для всех целых  , где   —  -ое число Фибоначчи, определяемое формулой:

Доказательство:

Докажем лемму по индукции: при  , что действительно верно. По индукции предполагаем, что  . Тогда

Лемма:

Фибоначчиево дерево порядка   содержит не менее   вершин.

Доказательство:

Докажем это утверждение по индукции. Пусть   — минимальный размер фибоначчиева дерева порядка n. При  . При  . (Можем удалить 1 ребенка) Предположим по индукции, что для всех  . Пусть в нашем дереве удалено поддерево порядка  (худший). Тогда Но по предыдущей лемме  . Следовательно,

Лемма:

Максимальная степень   произвольной вершины в фибоначчиевой куче с   вершинами равна

Доказательство:

Пусть   — произвольная вершина в фибоначчиевой куче с   вершинами, и пусть   — степень вершины  . Тогда по доказанному выше в дереве, корень которого  , содержится не менее   вершин, что в свою очередь по лемме равно  - доказывалось на лекции как очевидное . То есть (выполнено для поддерева ведь, значит это верно) Логарифмируя по основанию  , получаем Таким образом, максимальная степень   произвольной вершины равна  .

Система непересекающихся множеств. Алгоритм Крускала.

Алгоритм Крускала

Sort(E) – по возрастанию веса

Для каждого ребра e из E MakeSet(e)

For (u,v) из E (уже по возрастанию веса)

If (FindSet(u) != FindSet(v))

Union(u->Set, v->Set)

Оценка

До начала работы алгоритма необходимо отсортировать рёбра по весу, это требует O(E × log(E)) времени. После чего компоненты связности удобно хранить в виде системы непересекающихся множеств. Все операции в таком случае займут O(E × α(E, V)), где α — функция, обратная к функции Аккермана. Поскольку для любых практических задач α(E, V) < 5, то можно принять её за константу, таким образом общее время работы алгоритма Крускала можно принять за O(E * log(E)).

Система непересекающихся множеств

Эта структура данных предоставляет следующие возможности. Изначально имеется несколько элементов, каждый из которых находится в отдельном (своём собственном) множестве. За одну операцию можно объединить два каких-либо множества, а также можно запросить, в каком множестве сейчас находится указанный элемент. Также, в классическом варианте, вводится ещё одна операция — создание нового элемента, который помещается в отдельное множество.

Таким образом, базовый интерфейс данной структуры данных состоит всего из трёх операций:

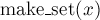•  — добавляет новый элемент 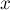 , помещая его в новое множество, состоящее из одного него.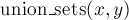

•  — объединяет два указанных множества (множество, в котором находится элемент  , и множество, в котором находится элемент  ).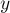

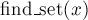•  — возвращает, в каком множестве находится указанный элемент  . На самом деле при этом возвращается один из элементов множества (называемый представителем или лидером (в англоязычной литературе "leader")). Этот представитель выбирается в каждом множестве самой структурой данных (и может меняться с течением времени, а именно, после вызовов  ).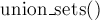

Например, если вызов   для каких-то двух элементов вернул одно и то же значение, то это означает, что эти элементы находятся в одном и том же множестве, а в противном случае — в разных множествах.

Описываемая ниже структура данных позволяет делать каждую из этих операций почти за   в среднем (более подробно об асимптотике см. ниже после описания алгоритма).

Определимся сначала, в каком виде мы будем хранить всю информацию.

Множества элементов мы будем хранить в виде деревьев: одно дерево соответствует одному множеству. Корень дерева — это представитель (лидер) множества.

При реализации это означает, что мы заводим массив  , в котором для каждого элемента мы храним ссылку на его предка в дерева. Для корней деревьев будем считать, что их предок — они сами (т.е. ссылка зацикливается в этом месте).