Фибоначчиева Куча
Фибоначчиево дерево — биномиальное дерево, где у каждой вершины удалено не более одного ребенка.
Порядок фибоначчиева дерева — порядок соответствующего биномиального дерева, из которого оно получено.
Степень вершины — количество дочерних узлов данной вершины.
Фибоначчиева
куча —
набор фибоначчиевых деревьев, корни
которых объединены в
неупорядоченный циклический двусвязный
список.
В отличие от биномиальной
кучи,
степени корней не обязаны быть попарно
различными.
Суть дерева в том, что любая операция,
которая не требует удаления элемента
из кучи, происходит за константу. Удаление
же происходит примерно за O(log(n))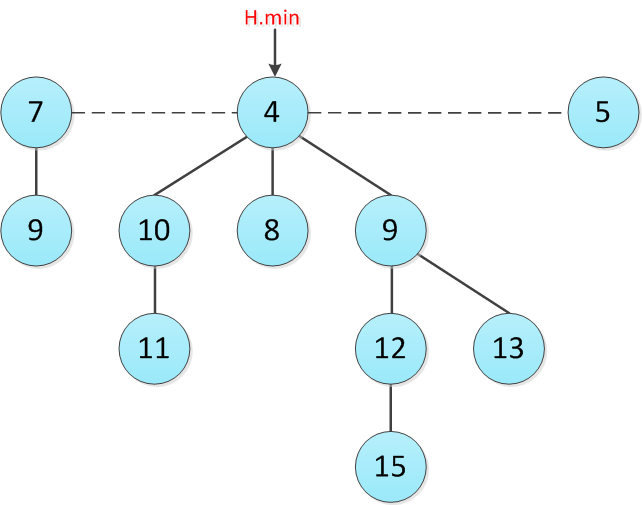
Пример
Фибоначчиево дерева.
Структура
Каждый узел
в
куче
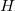содержит
следующие указатели и поля: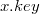
— поле, в котором хранится ключ;
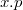— указатель на родительский узел;
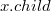— указатель на один из дочерних узлов
(левый) ;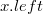
— указатель на левый сестринский узел;
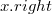— указатель на правый сестринский узел
;
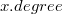— поле, в котором хранится количество
дочерних узлов;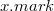
— логическое значение, которое
показывает, удаляли ли мы дочерние узлы
данной вершины.Дочерние узлы объединены при помощи указателей
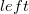и
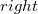в
циклический двусвязный список.Корни всех деревьев в связаны при помощи указателей и в циклический двусвязный список корней.
Порядок узлов – любой (в циклическом списке)
Обращение к выполняется посредством указателя
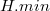на
корень дерева с минимальным ключом.
Этот узел называется минимальным узлом
.Текущее количество узлов в хранится в
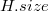.Максимальная степень
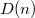произвольной
вершины в фибоначчиевой куче с
вершинами
равна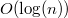 
Циклический двусвязный список обладает двумя преимуществами для использования в фибоначчиевых кучах. Во-первых, удаление элемента из такого списка выполняется за время . Во-вторых, если имеется два таких списка, их легко объединить в один за время Вводим потенциал:
Ф(Н) = t(H) + 2m(H) , где t(H) – число деревьев в корневом списке кучи, а m(H) – количество отмеченных вершин (mark == true)
Ф(H) >= 0 удовлетворяет условию использования потенциала. Если H – пустая куча, то == 0
Основные операции:
операция |
Ci - реальная стоимость |
Фi – Ф(i-1) |
|
|
0 |
|
|
1 |
|
|
0 |
|
|
0 |
|
|
D(n)+1+2m(H) |
|
|
|
|
|
|
makeHeap
Создается
новый пустой корневой список, в
устанавливается
значение
.
Реальное время работы —
.
insert
Вставка
элемента в фибоначчиеву кучу также
тривиальна: создается новая куча из
одного элемента и сливается с текущей.
Реальное время работы составляет
.
getMin
Возвращает указатель . Реальное время работы — .
merge
Слияние двух фибоначчиевых куч происходит просто: объединяем списки этих куч в один, релаксируем минимум. Реальное время работы — .
Ф(H) – (Ф(Н1) + Ф(Н2)) = t(H) – t(H1) – t(H2) + 2(m(H) – m(H1) – m(H2)) = 0
extractMin
Первая
рассматриваемая операция, в ходе которой
меняется структура кучи. Здесь используется
вспомогательная процедура
.
Возьмем указатель на
,
удалим эту вершину. Ее поддеревья (их
не более, чем
,
где
—
максимальная степень вершины в куче)
объединим с корневым списком. Теперь
вызываем процедуру
.
После этой операции в списке корней
остается не более чем
узлов, среди которых нужно найти
минимальный.
z = min(H)
if (z != null)
then
for каждый ребенок x вершины z
do добавить x в корневой список H
p[x] = null
удалить z из корневого списка H
if (z == right[z])
then min(H) = null
else
min(H) = right[z]
Consolidate(H)
Return z;
consolidate
Данная процедура принимает кучу и преобразует ее таким образом, что в корневом списке остается не более вершин.
Для
этого возьмем массив списков указателей
на корни деревьев
,
где
—
максимальная степень вершины в текущем
корневом списке.
Затем
происходит процесс, аналогичный слиянию
биномиальных куч: добавляем поочередно
каждый корень, смотря на его степень.
Пусть она равна
.
Если в соответствующей ячейке
еще
нету вершины, записываем текущую вершину
туда. Иначе подвешиваем одно дерево к
другому, и пытаемся также добавить
дерево, степень корня которого уже равна
.
Продолжаем, пока не найдем свободную
ячейку. Когда
подсоединяем x
к y,
убираем пометку с x
Учетная
стоимость
равна
.
Иначе говоря:
Если x->degree =d
Если A[d] == null, то A[d] = x
Иначе, если A[d] == y, то z = Link(x,y) – y станет сыном x, A[d] == null, аналогично далее. Когда подсоединяем x к y, убираем пометку с x
Учетная стоимость равна . Докажем это вместе с ExtractMin:
Нужно O(D(n)) действий, чтобы поместить детей удаляемой вершины в корень. Затем начальный и конечный этапы consolidate (создать массив A и, находя минимум, поместить деревья в корень) тоже за O(D(n)). Остальная часть consolidate – за O(D(n)) + O(число вызовов Link). Но при каждом вызове Link – длина корневого списка уменьшается на 1, а число отмеченных вершин может только уменьшиться. Так что умножим потенциал на подходящую константу общая сложность – O(D(n))
decreaseKey
Основная идея: хотим, чтобы учетная стоимость данной операции была . Было бы хорошо, чтобы вершина не всплывала до корня, и тогда дерево не придется сильно перестраивать. Для этого при удобном случае будем вырезать поддерево полностью и перемещать его в корневой список. Итак, сам алгоритм:
Проверяем, если новое значение ключа все же не меньше значения ключа родителя, то все хорошо, и мы выходим.
Иначе, вырезаем дерево с текущей вершиной в корневой список, и производим каскадное вырезание родителя.
If (k > key[x])
Error
Key[x] = k
y = p[x]
if (y != null && key[x] < key[y])
cut(H,x,y)
CascadingCut(H,y)
If (key[x] < key[min(H)])
Min(H) = x
cut
При
вырезании вершины мы удаляем ее из
списка детей своего родителя, уменьшаем
степень ее родителя (
),
добавляем вершину в корневой список H
и снимаем пометку с текущей вершины
(
).
cascadingCut
Перед
вызовом каскадного вырезания нам
известно, удаляли ли ребенка у этой
вершины. Если у вершины до этого не
удаляли дочерний узел (
),
то мы помечаем эту вершину (
)
и прекращаем выполнение операции. В
противном случае применяем операцию 
для
текущей вершины и запускаем каскадное
вырезание от родителя – для поддержки
инварианта из определения фибоначчиева
дерева
z = p[y]
if (z != null)
if (mark[y] == false)
mark[y] = true
else
cut(H,y,z)
CascadingCut(H,z)