Минимальное остовное дерево. Алгоритм Прима. Биномиальная куча.

Минимальное остовное дерево:

Дано дерево G=<V,E>

Задача: выкинуть ребра (оставить |V| - 1 ребро) так, чтобы граф был связным и имел минимальный возможный вес, где под весом дерева понимается сумма весов входящих в него рёбер. Тогда полученное дерево – минимальное остовное дерево.

Строим А – множество ребер

A = empty

While (A != MST)

Ищем безопасное ребро (u,v)

A = A + (u,v)

Инвариант: На каждом шаге алгоритма А – подмножество некоторых MST (их может быть много разных)

Безопасное ребро – такое, что при добавлении его к А – инвариант сохраняется

Разрез – разбиение графа на 2 множества (два графа) – S и V\S

Разрез согласован с A, если ни одно ребро из A не пересекает разрез

Легкое ребро – ребро, пересекающее разрез и имеющее наименьший вес из таких же.

Теорема: G=(V,E) – связный, неориентированный. A лежит в E. Есть разрез (S, V\S), согласованный с A. (u,v) – легкое ребро (S, V\S). Тогда (u,v) – безопасно для А

Док-во:

Покажем, что другой ситуации не может быть.

A лежит в T = MST. (u,v) не лежит в T. Иначе - тривиально

u и v в разных сторонах разреза  существует путь из u в v (ведь это ребро не лежит в T, а связность должна выполняться). Пусть ребро, пересекающее разрез в этом пути – (x,y).

w(u,v) < w(x,y) (по условию)  w(T + (u,v) - (x,y) = T’) <= w(T), но T – min  или T’ тоже MST и (u,v) – безопасно для А (MST может быть несколько), или, в другом случае, противоречие. Чтд

Алгоритм Прима

Алгоритм построения минимального остовного дерева (дерево, сумма весов ребер которого минимальна) Вход: взвешенный граф (неориентированный) Алгоритм:

1. Выбираем некоторую стартовую вершину

2. Из этой вершины строим самый дешевый путь

3. Берем связанные вершины и строим самые дешевые пути из них (не рассматриваем те, которые образуют цикл)

4. Продолжаем до тех пор, пока не свяжем все вершины

Примечания:

• Для быстрого нахождения минимальных путей рекомендуется использовать биномиальную кучу. (Например за приоритет вершины брать расстояние до текущего A – текущего подмножества MST)

• Интерпретация задачи: есть некое множество городов (и расстояний между ними) - нужно построить самую дешевую сеть дорого (самую короткую)

Сложность:

Способ представления графа и приоритетной очереди	Асимптотика
Массив d, списки смежности (матрица смежности)	O(|V|^2)
Бинарная пирамида, списки смежности	O(ElogV)
Фибоначчиева пирамида, списки смежности	O(E + VlogV)

Биномиальная куча

Описание: структура данных, реализующая абстрактный тип данных «Очередь с приоритетом», которая представляет собой набор биномиальных деревьев с двумя свойствами:

• ключ каждой вершины не меньше ключа ее родителя;

• все биномиальные деревья имеют разный размер.

Слoжность:

Make – O(1) Merge – O(logN) Insert – O(log N) – где N – количество элементов в куче. Minimum – O(log n) ExtractMin – O(log N) Decrease – O(log N) Delete – O(log N)

Биномиальное дерево – дерево, которое задается рекуррентно: Bi – это Bi-1, в котором левым сыном корня сделали дерево Bi-1. B0 — это просто вершина. Примеры для B0, B2, B3: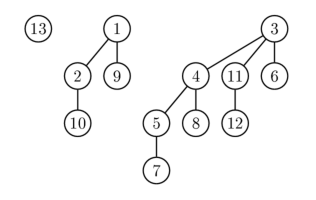 У биномиального дерева(Bk) есть ряд интересных свойств:

1. 2^k вершин: 2^(k-1) + 2(k-1) = 2^k

2. Высота дерева k (k – 1 – высота левого ребенка корня, + 1 – сам корень  k)

3. Cⁱ_k вершин глубины i – D(k,i) (вот почему они называются биномиальными: Cki биномиальный коэффициент).

D(k,i) = D(k-1,i) + D(k-1,i-1) = C(k-1)I + C(k-1)(i-1) = Cki – предпоследнее равенство по индукции.

4. Дети корня – это Bk-1, Bk-2, …, B0 – именно в этом порядке. - очевидно

5. Максимальная высота вершины в биномиальном дереве O(log N) – т.к. для числа N – строится B_logN дерево, а у него высота - logN.

Биномиальная куча – множество биномиальных деревьев, со следующими ограничениями:

1. В каждом из биномиальных деревьев сохраняется свойство неубывющей кучи.

2. Нет двух деревьев одинакового размера

3. Деревья упорядочены по размеру.

4. Для n элементов – не более logn + 1 деревьев (т.к. дерево этой степени вместит все n вершин)

Хранение: корневой список (root_list), его длина, в котором будут корни биномиальных деревьев, в порядке возрастания высоты. У каждой вершины будут следующие поля:

• data – данные, которые хранятся в вершине(по ним мы и находим минимум)

• right – правый брат

• child – левый сын

• degree– степень вершины (очевидно деревья в биномиальной куче упорядоченны по этому полю)

root_list.length = O(log N), где N — количество элементов в куче, т.к. в каждом дереве 2^k вершин, то есть в двоичном представлении числа <=logn разрядов, а каждое дерево представляет собой разряд

Операции: Make Задача: создать пустую кучу. Алгоритм: создаем пустой список root_list. Сложность: O(1). Merge Задача: объединить 2 кучи в 1. Алгоритм: сначала объединим корневые списки куч в 1 корневой список, поддерживая упорядоченность по degree. Алгоритм аналогичен слиянию 2-х массивов в mergeSort: Храним по указателю на начало списков и в результирующий список записываем минимальный из них, тот откуда только что записали сдвигаем на следующий. Далее проходимся от начала до конца нового полученного корневого списка и сливаем деревья одинакового размера в 1. Могут быть случаи:

1. Только 2 дерева одинакового размера. Тогда объединяем их.

2. 3 дерева одинакового размера. Объединяем 2 последних.

При объединении двух деревьев нужно лишь посмотреть в корне какого из них меньший ключ и сделать другое дерево левым сыном корня этого дерева. Пример, того, что получается после объединения двух куч: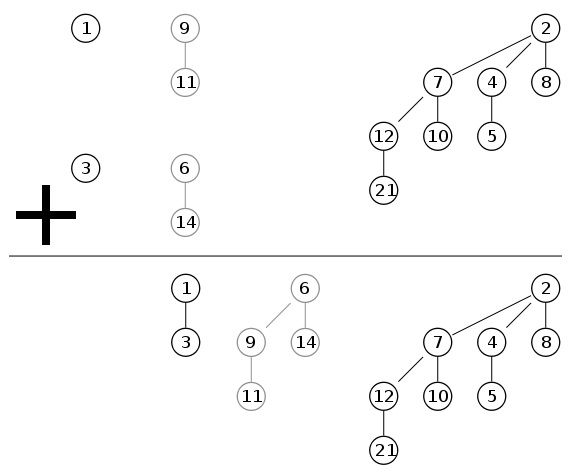 Сложность: Время работы O(root_list1.length) + O(root_list2.length) = O(log N). За один проход (O(log N )) мы получим объединенное биномиальное дерево. Получаем, что общая сложность O(log N). Insert Задача: вставить новый элемент в кучу. Алгоритм: Создаем кучу из одного элемента и объединяем с нашей кучей. Сложность: O(1) + O(log(N)) = O(log(N)). Minimum Задача: найти минимум в куче. Алгоритм: минимум находится в корневом списке, то есть, чтобы его найти нужно пройтись по корневому списку. Сложность: O(root_list.length) = O(log(N)). ExtractMin Задача: удалить минимальный элемент. Алгоритм: находим его при помощи Minimum. Удаляем его из корневого списка. Из перевернутого списка его детей делаем root_list для новой кучи и объединяем исходную кучу с H1. Сложность: так как каждая операция в извлечении минимума работает за O(log N): O(log N) + O(log N) + O(log N) = O(log N) DecreaseKey Задача: уменьшить значение key в данной вершине. Алгоритм: уменьшаем значение в вершине. Тогда свойство кучи будет возможно нарушено для нашей вершины и ее предка, тогда меняем их местами. Продолжаем процесс, пока наша вершина не “всплывет” на свое место. Алгоритм работает также, как аналогичный в двоичной куче. Сложность: В худшем случае наша вершина будет всплывать до корня, то есть мы совершим O(log N ) действий (вершина на каждом шаге “всплывает” на уровень выше, а высота биномиального дерева O(log N)) Delete Задача: удалить произвольный элемент. Алгоритм: сначала уменьшим при помощи Decrease значение в вершине до минимально возможного. А затем удалим минимальный в куче (ExtractMin). Сложность: O(log N) + O(log N) = O(log N)