Алгоритм a*. Эвристики.

Алгоритм поиска А*

Находит маршрут с наименьшей стоимостью от одной вершины (начальной) к другой (конечной) с использованием эвристической функцией. Вход: взвешенный граф, начальная вершина, конечная вершина. Выход: последовательность вершин от начальной вершины до конечной. Алгоритм: в каждой вершине есть поля h(x) - допустимая эвристическая оценка до конечной вершины (не превышает реального расстояния), g(x) - стоимость пути он начальной вершины, f(x) = g(x) + h(x). Алгоритм пошагово просматривает все пути, ведущие от начальной вершины в конечную, пока не найдет минимальный. В первую очередь он просматривает то алгоритмы, которые “кажутся” ведущими к цели, основываясь на значении функции f(x). В начале работы просматриваются вершины, смежные с данной, из них выбирается с минимальным значением f(x), после чего этот узел “закрывается” (помещается в множество “закрытых вершин”). На каждом этапе алгоритм работает с множеством “открытых вершин” (еще не пройденных), которые помещаются в очередь с приоритетом (приоритет по значению f(x)). Алгоритм продолжает свою работу до тех пор, пока значение f(x) целевой вершины не окажется меньшим, чем любое значение в очереди (либо пока всё дерево не будет просмотрено). Из множественных решений выбирается решение с наименьшей стоимостью.

Требования для эвристики (оценки)

1. h(u,t) <= b(u,t) – кратчайшее расстояние

2. h(a,c) <= h(a,b) + h(b,c)

Если сделать f(x) = g(x) – это Дейкстра.

Если всем вершинам сделать одинаковые, большие веса, а при доставании вершины из очереди уменьшать на 1 приоритет соседей – то будет BFS

Эвристики:

Поведение алгоритма сильно зависит от того, какая эвристика используется. В свою очередь, выбор эвристики зависит  от постановки задачи. Часто А* используется для моделирования перемещения по поверхности, покрытой координатной сеткой.

• Если мы можем перемещаться в четырех направлениях, в качестве эвристики стоит выбрать манхэттенское расстояние .

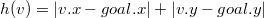• Расстояние Чебышева применяется когда к четырем направлениям добавляются диагонали: .

• Если передвижение не ограниченно сеткой, то можно использовать евклидово расстояние по прямой: .

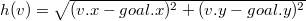Также стоит обратить внимание на то как соотносятся   и  . Если они измеряются в разных величинах (например,   — это расстояние в километрах, а   — оценка времени пути в часах) А* может выдать некорректный результат.

Псевдокод: OPEN = priority queue containing START CLOSED = empty set while lowest rank in OPEN is not the GOAL:  current = remove lowest rank item from OPEN  add current to CLOSED  for neighbors of current:    cost = g(current) + movementcost(current, neighbor)    if neighbor in OPEN and cost less than g(neighbor):      remove neighbor from OPEN, because new path is better    if neighbor not in OPEN and neighbor not in CLOSED:      set g(neighbor) to cost      add neighbor to OPEN      set priority queue rank to g(neighbor) + h(neighbor)      set neighbor's parent to current reconstruct reverse path from goal to start by following parent pointers

Если пишем пятнашки:

Манхэттенское расстояние (Manhattan distance)

Манхэттенское расстояние — это сумма расстояний по строкам и столбцам от текущего расположения костяшки до ее правильной позиции:

2

⇒

2

На этой схеме манхэттенское расстояние равно 4.

Линейный конфликт (Linear conflict)

Считается, что костяшка I и костяшка J находятся в линейном конфликте по строке, если они обе стоят в своей строке, но костяшка I находится левее костяшки J, хотя на самом деле должна быть справа:

15 13

⇒

13   15

На этой схеме I = 15, J = 13.

Мы должны подвинуть одну из костяшек со строки, поэтому можем добавить 2 к манхэттенскому расстоянию. Аналогичным образом рассматривается линейный конфликт по столбцу.

Угловые фишки (Corner tiles)

Рассмотрим правый верхний угол. Пусть «3» или «8» стоит на своей позиции, а на месте «4» — любая другая костяшка:

3 !4

!4       8

В таком случае, чтобы поставить «4» на место, костяшки придется подвинуть. Для этого добавим 2 к манхэттенскому расстоянию. Если «3» или «8» участвует в линейном конфликте (linear conflict), то двойка уже добавлена.

Аналогично с левым верхним и левым нижним углами. Правый нижний угол в эвристике не рассматривается, так как очень сложно скомбинировать этот случай с эвристикой «Последний ход».

Последний ход (Last move)

На последнем ходу мы либо двигаем костяшку «15» влево, либо «12» — вверх:

15

⇒

15

12

⇒

12

Если костяшки не находятся на требуемых позициях («15» — в крайнем правом ряду или «12» — в самой нижней строке), манхэттенское расстояние не учитывает переход через угол. Следовательно, мы можем добавить к нему 2.