Поиск со звездочками. Алгоритм Кнута-Морриса-Пратта.

Поиск со зведочками

Дан шаблон со звездочками (* - любой символ, но только 1), например ab*av**a (слово abqavqqa - подходит)

Как осуществлять поиск? Надо разбить шаблон на шаблоны без звезд (назовем массив таких шаблонов - runs). То есть в вышеописанном примере runs = {ab,av,a}. Кроме того будем хранить позицию начала этих шаблонов (без *) во всем шаблоне.

Создадим массив counts длины нашего текста. Изначально элементы равны в нем 0.

Затем запустим поиск в тексте всех шаблонов без * (из массива runs). Это будет происходить по очереди, если используем КМП, или сразу, если Ахо-Корасик. Затем будем делать counts[entry - runs[j].position]++, если j-ый шаблон из массива runs встретился в нашей строке на позиции entry

Потом мы пройдемся по массиву counts и все позиции в нем, где значение равно количеству шаблонов без * - это вхождения нашего шаблона (всего)

Алгоритм Кнута-Морриса-Пратта (КМП)

Введем понятие префикс-функции. Префикс-функция для i-ой позиции — это длина максимального префикса строки, который короче i и который совпадает с суффиксом префикса длины i. Если определение Z-функции не сразило оппонента наповал, то уж этим комбо вам точно удастся поставить его на место :) А на человеческом языке это выглядит так: берем каждый возможный префикс строки и смотрим самое длинное совпадение начала с концом префикса (не учитывая тривиальное совпадение самого с собой). Вот пример для «ababcaba»:

префикс	префикс	p
a	a	0
ab	ab	0
aba	aba	1
abab	abab	2
ababc	ababc	0
ababca	ababca	1
ababcab	ababcab	2
ababcaba	ababcaba	3

Самое первое значение префикс-функции, очевидно, 0. Пусть мы посчитали префикс-функцию до i-ой позиции включительно. Рассмотрим i+1-ый символ. Если значение префикс-функции в i-й позиции P_i, то значит префикс A[..P_i] совпадает с подстрокой A[i-P_i+1..i]. Если символ A[P_i+1] совпадет с A[i+1], то можем спокойно записать, что P_i+1=P_i+1. Но вот если нет, то значение может быть либо меньше, либо такое же. Конечно, при P_i=0 сильно некуда уменьшаться, так что в этом случае P_i+1=0. Допустим, что P_i>0. Тогда есть в строке префикс A[..P_i], который эквивалентен подстроке A[i-P_i+1..i]. Искомая префикс-функция формируется в пределах этих эквивалентных участков плюс обрабатываемый символ, а значит нам можно забыть о всей строке после префикса и оставить только данный префикс и i+1-ый символ — ситуация будет идентичной. 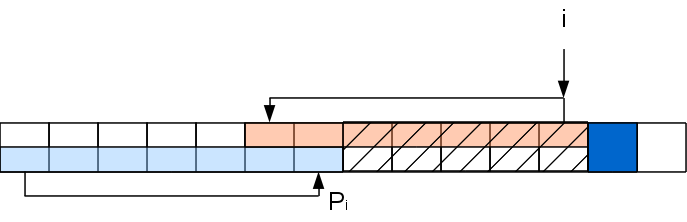Задача на данном шаге свелась к задаче для строки с вырезанной серединкой: A[..P_i]A[i+1], которую можно решать рекурсивно таким же способом (хотя хвостовая рекурсия и не рекурсия вовсе, а цикл). То есть если A[P_Pi+1] совпадет с A[i+1], то P_i+1=P_Pi+1, а иначе снова выкидываем из рассмотрения часть строки и т.д. Повторяем процедуру пока не найдем совпадение либо не дойдем до 0. 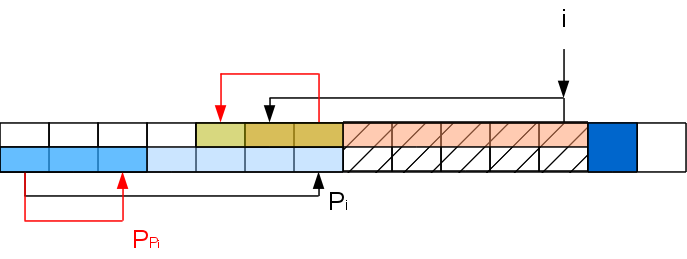Повторение этих операций должно насторожить — казалось бы получается два вложенных цикла. Но это не так. Дело в том, что вложенный цикл длиной в k итераций уменьшает префикс-функцию в i+1-й позиции хотя бы на k-1, а для того, чтобы нарастить префикс-функцию до такого значения, нужно хотя бы k-1 раз успешно сопоставить буквы, обработав k-1 символов. То есть длина цикла соответствует промежутку между выполнением таких циклов и поэтому сложность алгоритма по прежнему линейна по длине обрабатываемой строки. С памятью тут такая-же ситуация, как и с Z-функцией — линейная по длине строки, но есть способ сэкономить. Кроме этого есть удобный факт, что символы обрабатываются последовательно, то есть мы не обязаны обрабатывать всю строку, если первое вхождение мы уже получили. prefFunction(_pattern.size()), pattern(_pattern)

{

prefFunction[0] = 0;

long long q = 0;

for (size_t i = 1; i < pattern.size(); i++)

{

while (q > 0 && pattern[i] != pattern[q])

q = prefFunction[q - 1];

if (pattern[i] == pattern[q])

q++;

prefFunction[i] = q;

}

Алгоритм КМП осуществляет поиск подстроки в строке. Условия: Даны образец и строка . Требуется определить индекс, начиная с которого строка содержится в строке . Если не содержится в — вернуть индекс, который не может быть интерпретирован как позиция в строке (например, отрицательное число). При необходимости отслеживать каждое вхождение образца в текст имеет смысл завести дополнительную функцию, вызываемую при каждом обнаружении образца. Алгоритм: Рассмотрим сравнение строк на позиции , где образец сопоставляется с частью текста . Предположим, что первое несовпадение произошло между и , где . Тогда и . При сдвиге вполне можно ожидать, что префикс (начальные символы) образца сойдется с каким-нибудь суффиксом (конечные символы) текста . Длина наиболее длинного префикса, являющегося одновременно суффиксом, есть префикс-функция от строки для индекса . Это приводит нас к следующему алгоритму: пусть — префикс-функция от строки для индекса . Тогда после сдвига мы можем возобновить сравнения с места и без потери возможного местонахождения образца.