Ответы на запросы
Ответы
на запросы будут происходить за время
.
Для ответа на запрос заметим сначала,
что если
,
для некоторых
и
,
то
.
Поэтому если
,
то пройдем от вершины
на
шагов
вверх, это и будет новое значение
и
это можно сделать за
.
Можно записать число
в
двоичной системе, это представление
этого число в виде суммы степеней двоек,
и
для всех
пройти
вверх последовательно из вершины
в
.
Дальше
считаем, что
.
Если
,
то ответ на запрос
.
А
если
,
то найдем такие вершины
и
,
такие что
,
—
предок
,
—
предок
и
.
Тогда ответом на запрос будет
.
Научимся
находить эти вершины
и
.
Для этого сначала инициализируем
и
.
Дальше на каждом шаге находим такое
максимальное
,
что
.
И проходим из вершин
и
на
шагов
вверх. Если такого
найти нельзя, то значения
и
,
это те самые вершины, которые нам
требуется найти, ведь
.
Оценим
время работы. Заметим, что найденные
строго
убывают. Во-первых, потому что мы находим
на каждом шаге максимальное значение
,
а во-вторых, два раза подряд мы одно и
то же
получить
не можем, так как тогда получилось бы,
что можно пройти
шагов,
а значит вместо первого
,
мы бы нашли
.
А значит всего
значений
,
их можно перебирать в порядке убывания.
Сложность ответа на запрос
.
Псевдокод
preprocess()
p
:= dfs(0)
for i := 1 .. n
dp[i][0]
:= p[i]
for j := 1 .. log(n)
for
i := 1 .. n
dp[i][j] :=
dp[dp[i][j - 1]][j - 1]
lca(v,
u)
if (d[v] > d[u])
swap(v,
u)
for i := log(n) .. 0
if
(d[u] - d[v] >=
)
u
:= dp[u][i]
if (v = u)
return
v
for i := log(n) .. 0
if
(dp[v][i] <> dp[u][i])
v
:= dp[v][i]
u :=
dp[u][i]
return p[v]
Алгоритм с предпроцессингом (Сведение LCA к RMQ) Для каждой вершины определим глубину с помощью следующей рекурсивной формулы:
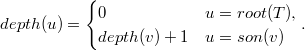Ясно,
что глубина вершины элементарным
образом поддерживается во время обхода
в глубину.
Запустим
обход в глубину из корня, который будет
вычислять значения следующих величин:
Cписок глубин посещенных вершин . Глубина текущей вершины добавляется в конец списка при входе в данную вершину, а также после каждого возвращения из её сына.
Список посещений узлов
,
строящийся аналогично предыдущему,
только добавляется не глубина а сама
вершина.Значение функции
,
возвращающей любой индекс в списке
глубин
,
по которому была записана глубина
вершины
(например
на момент входа в вершину).
Запрос
Будем
считать, что
возвращает
индекс минимального элемента в
на
отрезке
.
Тогда ответом на запрос
,
где
,
будет
.
RMQ через LCA
Дан
массив 
.
Поступают запросы вида 
,
на каждый запрос требуется найти минимум
в массиве
,
начиная с позиции
и
заканчивая позицией
.
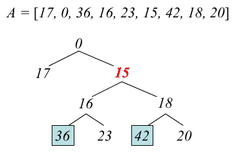
Алгоритм
Декартово дерево (англ. сartesian tree) по неявному ключу на массиве — это бинарное дерево, допускающее следующее рекурсивное построение:
Корнем дерева является элемент массива, имеющий минимальное значение , скажем
.
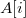Если минимальных элементов несколько,
можно взять любой.Левым поддеревом является декартово дерево на массиве
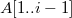.Правым поддеревом является декартово дерево на массиве
.
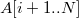Здесь и далее будет также использоваться для обозначения соответствующей вершины дерева.
Построим
декартово дерево на массиве
.
Тогда 
= 
.