1. 

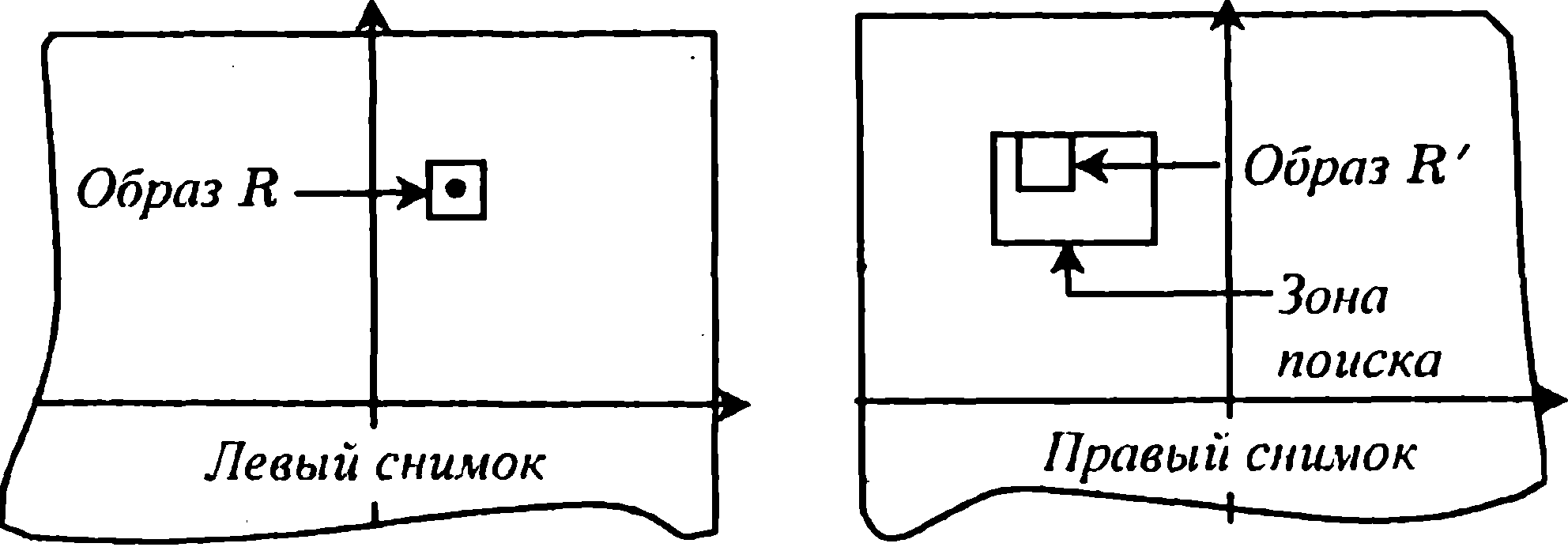
   Рис. 14.13. К автоматической идентификации точек

   Выбрать на левом снимке образ R в виде области размером пхп пикселов, в центре которой размещена опознаваемая точка (рис. 14.13), и определить его характеристику-эталон, на основе кото­рой будет выполняться проверка условия (14.9).

2. Определить на правом снимке зону поиска размером тхпг пик­селов (т»п) вероятного расположения искомой точки с коор­динатами центра хп & хл - Ьсю уп & ул (рис. 14.13).

3. Последовательным перемещением области размером пхп в гра­ницах зоны поиска на один пиксел вначале по оси х, а затем по

272

оси у создать на правом снимке серию образов R и определить характеристики каждого из них. 4. Сопоставить характеристики каждого образа R с характеристи­кой-эталоном вектора R. Искомая точка на правом снимке будет расположена в центре образа R , для которого выполняется ус­ловие (14.9). Установление степени соответствия векторов R и R представляет основную трудность и может быть выполнено различными путями, из которых наиболее распространенным является расчет коэффициентов корреляции между яркостями элементов образа R и каждого из обра­зов R на правом снимке с использованием формулы:

-₌ Zfa-PoXPi-Pi) ^ ₍₁₄₁₀₎

VKpi - Ро)^{2 х} >Щр! - Ро)²

где ро и р'о - средние яркости элементов зон (фрагментов), соответст­вующих образам левого (Л) и правого (R) снимков.

Коэффициенты, подсчитанные для сочетаний образа R со всеми образами R\ образуют корреляционную матрицу: максимальное зна­чение ее элемента соответствует наиболее тесной связи яркостей срав­ниваемых участков левого и правого снимков, и, следовательно, вы­полнению условия (14.9). Так что искомая точка лежит в центре об­раза i?' с максимальным коэффициентом корреляции.

Некоторые способы предполагают отыскание искомой точки по максимуму корреляционной функции, составленной на основе анализа элементов корреляционной матрицы с частными коэффициентами корреляции (14.10), соответствующей искомому образу R .

Размер области снимка, отождествляемой с образом R, обычно со­ставляет 21x21 пиксел; при малом числе контуров местности он уве­личивается до 41x41 пикселов. Программы обработки обычно запра­шивают полуразмер корреляционной матрицы (образа R).

Размер области поиска на правом снимке выбирается таким, чтобы ом был больше ожидаемого смещения точки из-за влияния рельефа местности, подсчитываемого по формуле (3.40). Так, при Н = 2000 м, h. = 50 м г = 100 мм будем иметь 8д = 2,5 мм, а размер области поис­ка - минимум 5x5 мм.

Рассмотренный алгоритм позволяет отождествить точку на правом снимке с точностью, не превышающей одного пиксела. Для точных фотограмметрических измерений этого недостаточно, и для ее увели-

273

чения выполняют второй прием поиска с уменьшенным в k раз разме­ром пиксела и соответственно меньшей областью поиска.

Используемые в настоящее время способы автоматического ото­ждествления точек аэроснимков основаны на более или менее строгом анализе яркостей и геометрического положения элементов изображе­ния, и их надежность всецело определяется метрическими и изобрази­тельными свойствами изображений, особенностями контурной на­грузки и т.п. Все это предопределяют целесообразность стереоскоп пического контроля положения измерительной марки после работы кор­релятора, особенно при обработке снимков малоконтурной местности. В большинстве случаев опытный наблюдатель ее обязательно чуть-чуть подправит по высоте.

Кроме того, смещения точек, вызванные влиянием угла наклона снимка и рельефа местности, вызывают смещения отдельных элемен­тов растра, что меняют рисунок изображения и это не может не сказы­ваться на качестве идентификации.

Так, если на левом снимке образ R всегда представлен квадратом, то на правом снимке из-за влияния угла наклона и рельефа местности со­ответствующие элементы образа R получают смещения, и в общем слу­чае образуют контур многоугольника. Поскольку анализируемый образ R геометрически не всегда подобен образу Д, то вероятность полного совпадения искомой точки уменьшается. Еще более сложная ситуация возникает в случае, если изображения левого и правого снимков раз­вернуты одно относительно другого. Правда, из-за малости элементов изображения влияние перечисленных источников искажений не столь значительны, а их влияние можно компенсировать геометрической кор­рекцией положения пика корреляции и соответствующей ему точки правого снимка. Одно из таких решений основано на том, что смещения элементов образа являются следствием влияния рельефа в пределах со­ответствующего участка местности и интерпретируются как параллак­тические смещения .

В системах цифровой обработки изображений достаточно широко применяется еще один способ для идентификации точек снимков, сущ­ность которого заключается в следующем.

Поскольку перекрывающиеся части смежных снимков являются проекциями одного и того же участка местности, полученными из раз­ных центров, то перекрывающиеся изображения пары смежных сним­ков проективны, и для преобразования их координат правомерно при­менение формул проективного преобразования (4.1):

Книжников Ю. Ф., Гельман Р. Н. О некоторых источниках погрешностей при автома­тическом измерении цифровых стереопар // Геодезия и картофафия. 2000. № 5. с. 25-31.

274

А,*'	+ A2y'	+ AA
Ctx Btx'	' + C,y + B2y'	+ 1 + bA
Cxx	' + C,y	+ 1 J

где х', у',х, у - координаты точек, отнесенные к плоскостям левого и правого снимков соответственно; At, B_it C_t - параметры проективного преобразования.

Зависимости (14.11) содержат восемь неизвестных параметров преобразования, для определения которых достаточно измерить на смежных снимках координаты четырех пар соответственных точек, составить восемь уравнений поправок, решение которых позволяет отыскать параметры А/, В*, C_if после чего они могут быть использова­ны для идентификации любых других точек обрабатываемых снимков. Возможности рассмотренного способа ограничиваются влиянием рельефа местности.

Отождествление соответственных точек аэроснимков является ба­зовым процессом технологии как машинного зрения, так и цифровой фотограмметрии, и ее совершенствованию уделяется большое вни­мание. Сегодня имеется целый ряд способов решения этой задачи, ос­нованных на использовании уравнений базисных (эпиполярных) ли­ний, метода пирамид (HRC), метода вертикальной линии (ULL), мето­да динамического программирования и др.; активно разрабатывается метод структурной (реляционной) корреляции, устанавливающей со­ответствия между элементами сопоставляемых структурных описаний. Практическое применение этих методов позволит в перспективе пол­иостью автоматизировать процесс отождествления точек снимков.

Заметим, что если точность монокулярного измерения координат точек цифровых снимков ограничивается их геометрическим разреше­нием, то точность их идентификации и измерения координат на смеж­ном снимке всегда может быть выполнена с субпиксельной (подпик-ссльной) точностью, что и объясняет высокую точность фотограммет­рических обработки цифровых изображений.