3.2.3. Энергетические показатели при работе клистрона в усилительном режиме и режиме умножения частоты

Для прямолинейного движения электрона в переменном поле уравнение движения имеет вид:

, или .

Мощность взаимодействия с полем напряженности Е одного электрона на пути dx, равная изменению кинетической энергии электрона в единицу времени, будет определяться следующим выражением:

.

Если n – концентрация электронов, то находящиеся на пути dx электроны (N = ndx) создадут мощность взаимодействия

.

При гармоническом характере изменения переменных величин средняя за период мощность взаимодействия на пути l определяется из выражения

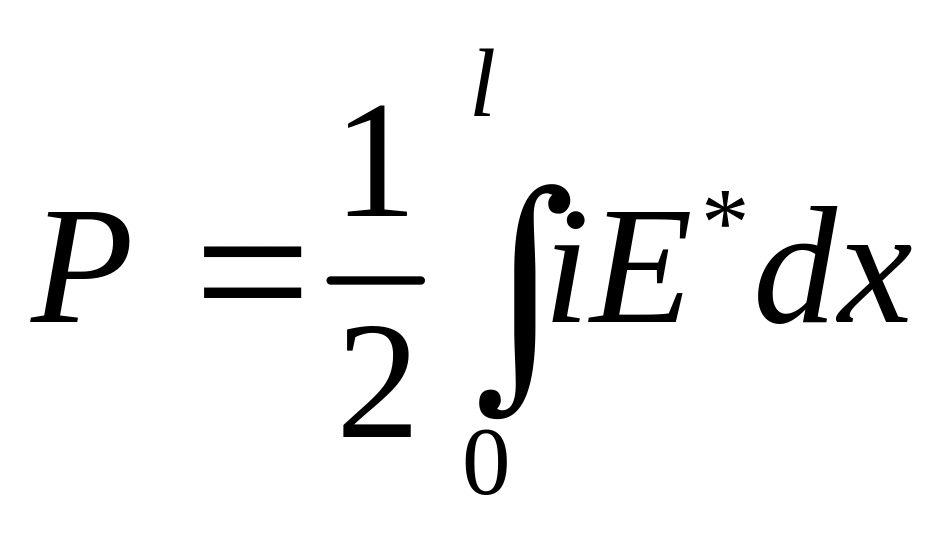, (3.15)

где i – комплексная амплитуда тока,

Е^* – комплексная сопряженная амплитуда поля.

Активная Р_а и реактивная Р_r мощности взаимодействия примут следующий вид:

;

,

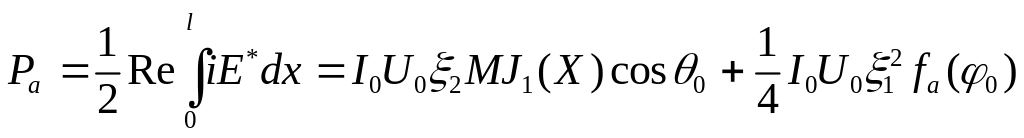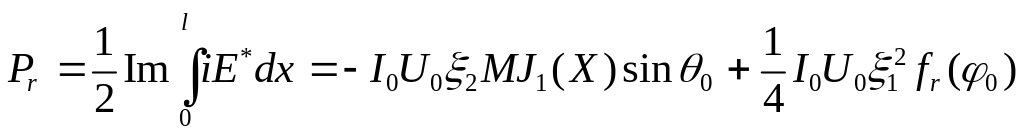где , ; U₁ – амплитуда СВЧ напряжения в модулирующем зазоре; U₂ – амплитуда СВЧ напряжения в промежутке взаимодействия выходного резонатора; U₀ – ускоряющее напряжение, создаваемое источником постоянного напряжения; f_a и f_r – монотронные функции, определяющие эффект конечного угла пролета в модулирующем зазоре [10]. При вторыми слагаемыми в выражениях для мощностей можно пренебречь:

; (3.16)

. (3.17)

Из (3.16) следует, что в зависимости от угла пролета невозмущенными электронами пространства дрейфа, взаимодействие модулированного по плотности электронного потока с СВЧ полем выходного резонатора может характеризоваться либо передачей энергии полю, либо наоборот – поле отдает энергию электронам. Если , то Р_а < 0 и электроны отдают энергию полю. Если , то Р_а > 0 и электроны получают энергию от поля, которая идет на увеличение их кинематической энергии. Качественно энергообмен электронного пучка с электромагнитным полем резонатора показан на рис. 3.9.

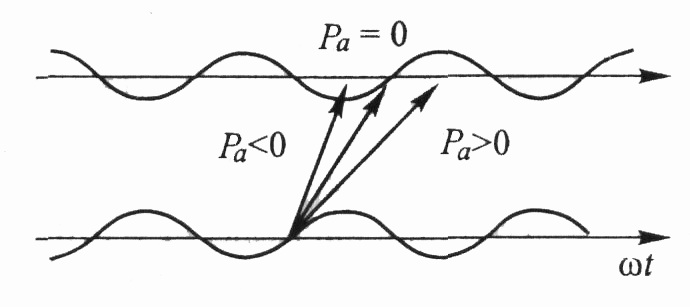
Рис. 3.9. Схема, поясняющая энергообмен электронного пучка и электромагнитного поля в выходном резонаторе пролетного клистрона [10]

Если сгусток проходит зазор в течение отрицательного полупериода, то электроны тормозятся, их кинетическая энергия уменьшается, Р_а < 0, а энергия поля увеличивается. При прохождении зазора в положительный полупериод электроны ускоряются, их кинетическая энергия возрастает, Р_а > 0, а энергия поля уменьшается.

Заметим, что реактивная компонента электронной мощности взаимодействия (3.17) сдвинута по фазе на угол относительно Р_а, то есть когда значение Р_а максимально, значение величины P_r равно нулю и наоборот.

Максимальный электронный КПД двухрезонаторного клистрона определяется из выражения

;

. (3.18)

Подбирая оптимальные значения углов пролета (cos = 1), параметра группировки (Х = 1,84) и полагая М 1, U₂ = U₀ (это соответствует максимальной амплитуде напряжения, так как при дальнейшем увеличении U₂ электроны будут отражаться обратно в пространство дрейфа), получим максимальный КПД, равный 58%.

Как уже отмечалось, пролетный клистрон может быть эффективно использован как умножитель частоты. В табл. 3.1 приведены значения отношений максимальных амплитуд гармоник i_n к постоянной составляющей тока I₀ и к первой гармонике i₁.

Таблица 3.1

n	1	2	3	5	10	15	20
in/I0	1,16	0,96	0,86	0,74	0,60	0,54	0,48
in/i1	1,00	0,83	0,75	0,64	0,52	0,47	0,42

Из таблицы следует, что максимальная величина амплитуды гармоники убывает медленно с ростом номера гармоники. Это позволяет использовать клистрон как эффективный умножитель частоты входного сигнала, при этом выходной резонатор настраивается на частоту заданной кратности.