3.2.2. Ток в пролетном клистроне

Выражение (3.3) для модулированного по скорости электронного потока получено в предположении нулевого времени пролета пространства взаимодействия входного резонатора и . Если время пролета или, что тоже самое, угол пролета конечен, то для нахождения закона модуляции необходимо проинтегрировать уравнение движения электрона в поле модулирующего зазора, протяженностью d, [10]

(3.4)

при начальных условиях , , .

В случае слабого сигнала ( ) имеет место следующее приближенное выражение:

, (3.5)

где – невозмущенный угол пролета (угол пролета в отсутствии СВЧ поля);

– (3.6)

параметр эффективности модуляции. Вид зависимости показан на рис. 3.6.

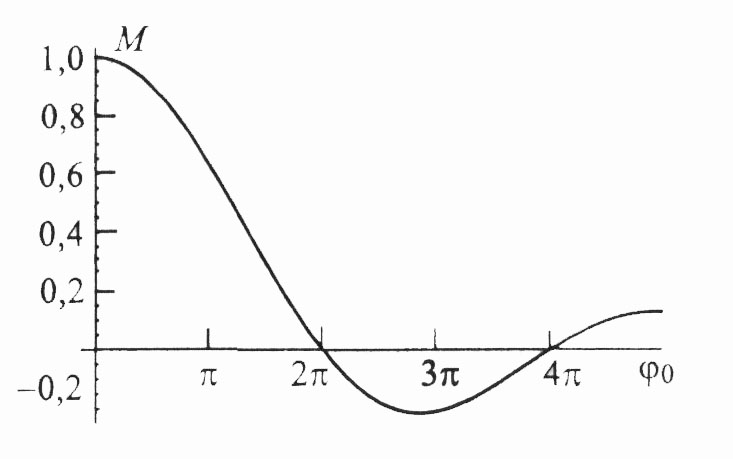
Рис. 3.6. Зависимость параметра эффективности модуляции от невозмущенного угла пролета .

Выражение (3.5) является приближенным, однако при малых, но конечных значениях , оно достаточно хорошо описывает скоростную модуляцию. При значение М = 1 и выражение (3.5) сводится к ранее полученному для скоростной модуляции (3.3).

В связи с технологическими трудностями невозможно сколь угодно уменьшать зазор модулятора d, а следовательно, величину невозмущенного угла пролета для достижения максимального значения параметра эффективности модуляции. В реальных пролетных клистронах , что соответствует М 0,9…0,6.

Для нахождения зависимости тока в клистроне от эффективности модуляции и протяженности дрейфового пространств найдем угол пролета электрона до некоторой плоскости, находящейся на расстоянии l от середины модулятора. Время прибытия электронов в данную плоскость равно

.

При малом параметре выражение . Тогда можно использовать приближение , . С учетом этого замечания выражение для времени пролета примет вид

,

а угол пролета

. (3.7)

В выражении (3.7) величина

(3.8)

называется параметром группирования электронного потока в сгустки; – угол пролета невозмущенными электронами пространства дрейфа длиной l; t₁ – время влета электронов в середину модулятора, от которой отсчитывается l (см. рис. 3.4, а). Несмотря на то, что , параметр группирования может быть и не малым, так как может принимать любые значения.

Определим теперь зависимость модулированного по плотности тока от времени на расстоянии l от середины модулятора. Полагаем, что I₀ – ток электронной пушки известен. На основании закона сохранения заряда для слоя электронов, проходящих плоскость X = 0 за время dt₁, а затем плоскость X = l за время dt можно записать

,

откуда для модулированного по плотности тока получаем

.

Дифференцируя (3.7) по переменной t₁, находим

. (3.9)

На рис. 3.7 представлены зависимости модулированного по плотности тока от начальной фазы влета в пространство дрейфа для различных значений параметра группирования.

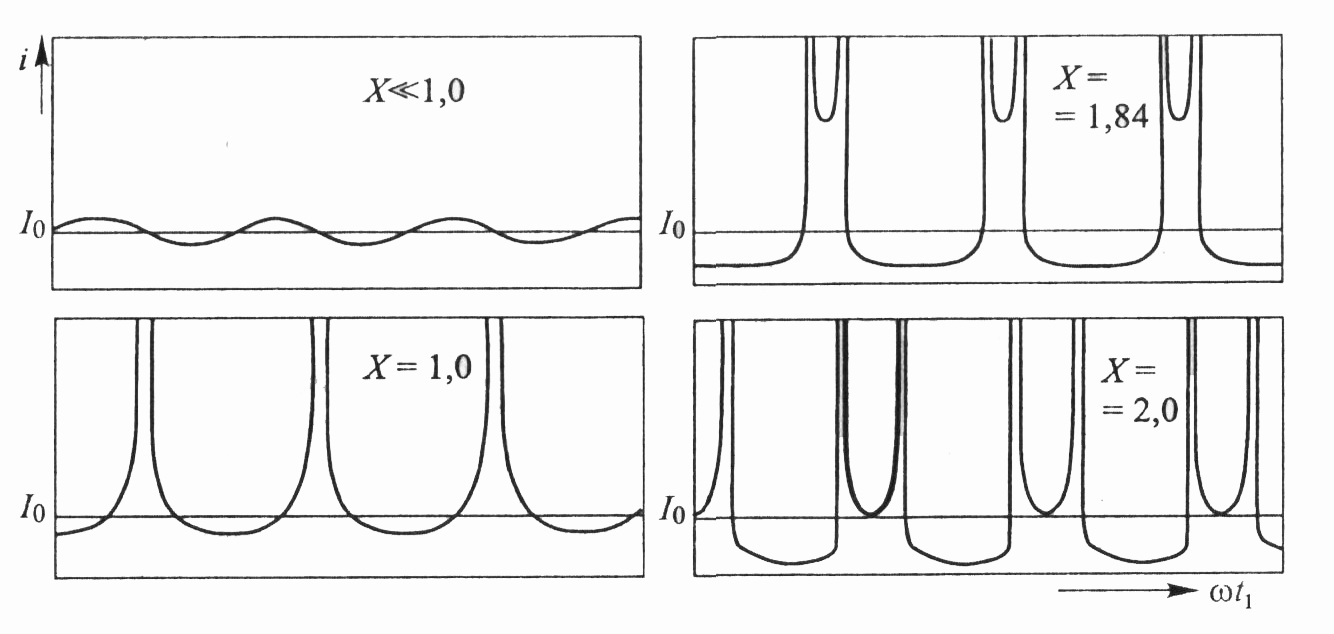
Рис. 3.7. Зависимость тока пучка от начальной фазы влета электронов для различных значений Х [10]

При из (3.9) получаем

. (3.10)

При Х = 1 знаменатель в (3.9) обращается в нуль при , где n = 1, 2, 3,…, а ток – в бесконечность (такой физический результат получается без учета кулоновских сил расталкивания электронов в сгустке, приводящих к размыванию сгустка). При X > 1 имеет место два максимума за период, которые при Х = 2 обращаются в бесконечность.

Так как ток является периодической функцией времени, то эту функцию можно представить в виде ряда Фурье.

,

где А_n – амплитуды гармоник, определяемые выражением

; (3.11)

– (3.12)

постоянная составляющая тока.

Подставляя выражения для (3.7) и тока (3.9) в (3.11), получим

, (3.13)

где – функция Бесселя первого рода n-ого порядка.

В результате спектр тока (3.9) будет иметь вид

. (3.14)

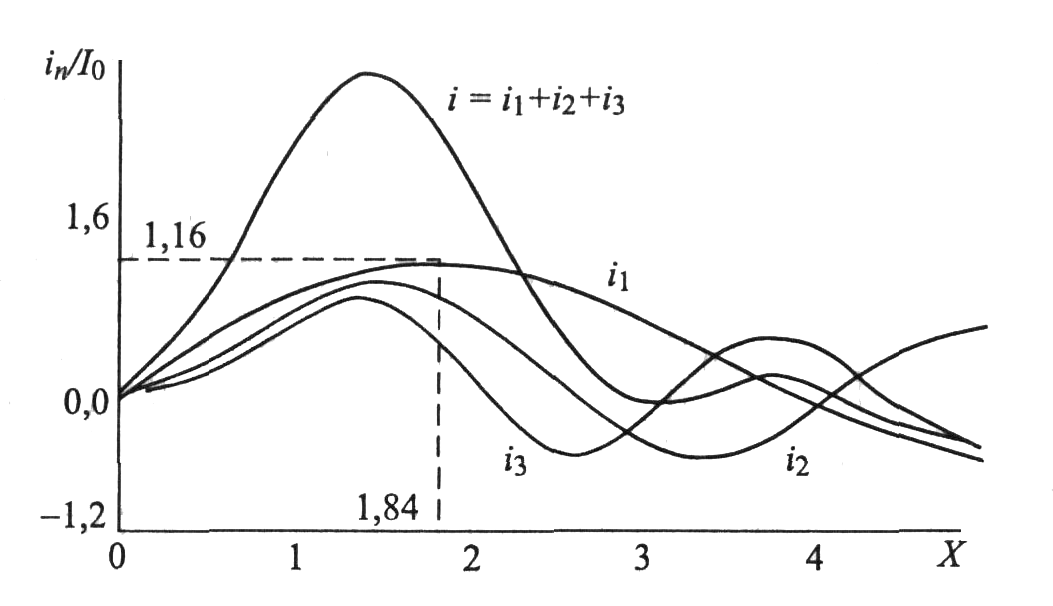
Рис. 3.8. Зависимости амплитуд гармоник сгруппированного тока от величины параметра группирования [10]

Из графических зависимостей на рис. 3.8 следует, что максимум амплитуды первой гармоники приходится на параметр группирования Х = 1,84 и составляет 1,16I₀, то есть имеет величину порядка постоянной составляющей тока пучка. Максимумы амплитуд второй и третьей гармоник не существенно отличаются от максимума амплитуды первой гармоники, что имеет значение при работе пролетного клистрона в режиме умножения частоты входного сигнала.