Вопрос 11

Теория

Существует несколько вариантнов определения компланарности трех векторов в пространстве. Приведем основные из них.

Три вектора называются компланарными, если они, будучи приведенными к общему началу, лежат в одной плоскоти.

Три вектора называются компланарными, если они лежат на параллельных плоскостях или на одной плоскости.

Три вектора называются компланарными, если имеются равные им вектора, параллельные одной плоскости.

Для трех векторов верны следующие утверждения:

если из трех векторов два коллинеарны, то эти тре вектора компланарны;

смешанное произведение трех компланарных векторов равно 0 (нулю) - это критерий компланарности трех векторов.

Смешанное произведение трех векторов a=(x_a,y_a,z_a), b=(x_b,y_b,z_b) и c=(x_c,y_c,z_c) вычисляется по следующей формуле:

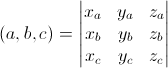
Если это произведение равно 0, то векторы компланарны

Разложение вектора в пространстве по трем некомпланарным векторам

Эта теорема есть частный случай более общего утверждения: любые линейно независимых векторов образуют базис в -мерном векторном пространстве.

На прямой (одномерное пространство) --- это любой ненулевой вектор, на плоскости (двумерное пространство) --- два любых неколлинеарных вектора, в изучаемом в школьном курсе стереометрии трехмерном пространстве --- три любых некомпланарных вектора.

Редактор [Редактор]

Математически верная формулировка

Если дана упорядоченная тройка векторов некомпланарных векторов, то для любого вектора существует единственная упорядоченная тройка чисел , удовлетворяющая равенству .

Вопрос 12

Скалярным произведением двух векторов называется число, равное произведению модулей этих векторов на косинус угла между ними.

Скалярное произведение векторов , обозначается символом (порядок записи сомножителей безразличен, то есть ).

Если угол между векторами , обозначить через , то их скалярное произведение можно выразить формулой

(1)

Скалярное произведение векторов , можно выразить также формулой

, или .

Из формулы (1) следует, что , если - острый угол, , если - тупой угол; в том и только в том случае, когда векторы и перпендикулярны (в частности, , если или ).

Скалярное произведение называется скалярным квадратом вектора и обозначается символом . Из формулы (1) следует, что скалярный квадрат вектора равен квадрату его модуля:

.

Если векторы и заданы своими координатами:

, ,

то их скалярное произведение может быть вычислено по формуле

.

Отсюда следует необходимое и достаточное условие перпендикулярности двух векторов

.

Угол между векторами

, ,

дается формулой , или в координатах

.

Проекция произвольного вектора на какую-нибудь ось u определяется формулой

,

где - единичный вектор, направленный по оси u. Если даны углы , , , которые оси u составляет с координатными осями, то и для вычисления вектора может служить формула

.