42. Время восстановления и характеристики его распределения. Вероятностные и статистические методы определения характеристик.

Время восстановления - это время, затраченное на обнаружение, поиск причины отказа и устранения последствий отказа. Опыт показывает, что в сложных электроустановках (системах) 70-90% времени восстановления приходится на поиск отказавшего элемента.

Среднее время восстановления - это математическое ожидание времени восстановления работоспособного состояния объекта после отказа . Из определения следует, что 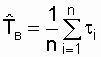, (2.17) где n - число восстановлений, равное числу отказов;  - время, затраченное на восстановление (обнаружение, поиск причины и устранение отказа), в часах. Показатель  можно определить и на основании статистических данных, полученных для М однотипных восстанавливаемых объектов. Структура расчетной формулы остается той же: 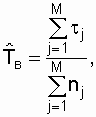(2.18) где М - количество однотипных объектов, для каждого из которых определено общее время восстановления  за заданное время наблюдений; 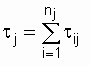 , где  - время восстановления j-го объекта после i-го отказа; nj - количество восстановлений j-го объекта за время наблюдений, причем  .

Интенсивность восстановления - это отношение условной плотности вероятности восстановления работоспособного состояния объекта, определенной для рассматриваемого момента времени при условии, что до этого момента восстановление не было завершено, к продолжительности этого интервала.

Статистическая оценка этого показателя находится как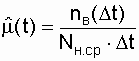 , (2.19)

где nв(Dt) - количество восстановлений однотипных объектов за интервал Dt;  - среднее количество объектов, находящихся в невосстановленном состоянии на интервале Dt.

В частном случае, когда интенсивность восстановления постоянна, то есть m(t) =m= const, вероятность восстановления за заданное время t подчиняется экспоненциальному закону и определяется по выражению . (2.20)

Этот частный случай имеет наибольшее практическое значение, поскольку реальный закон распределения времени восстановления большинства электроэнергетических объектов (поток восстановлений) близок к экспоненциальному [10, 14]. Используя свойства этого распределения, запишем очень важную зависимость:

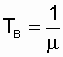, а также 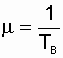 . (2.21)

43. Срок сохраняемости и характеристики его распределения. Вероятностные и статистические методы определения характеристик. Сохраняемость - свойство объекта сохранять в заданных пре­делах значения параметров, характеризующих способность объекта выполнять требуемые функции, в течение и после хранения и (или) транспортировки.  Проблема сохраняемости обостряется в связи с хранением большинства сельс­кохозяйственных машин на открытых площадках. Атмосферный воздух почти всегда загрязнен различными примесями, многие из которых агрессивны. Существенное влияние на коррозию металлов оказывает содержание в воздухе даже ничтожного количества сер­нистого газа и хлоридов, которые при растворении в воде образуют электролиты.

Продолжительность хранения  и транспортировки  иногда  не оказывает заметного влияния на поведение объекта во время на­хождения в этих режимах, но при последующей работе их свойства могут быть значительно ниже, чем аналогичные свойства объектов, но не находившихся на хранении и не подлежащих транспортиров­ке. Например, после продолжительного хранения аккумуляторных батарей их наработка до отказа существенно снижается. Сохраняе­мость таких объектов обычно характеризуется таким сроком хране­ния в определенных условиях, в течение которого снижение сред­ней наработки до отказа, обусловленное хранением, находится в допустимых пределах.

Вследствие воздействия внешней среды на незащищенные со­ставные части машин во время хранения сокращаются сроки их службы, увеличиваются затраты на ремонт.

Сохраняемость оценивают сроком сохраняемости. Срок сохраняемости - календарная продолжительность хранения и (или) транспортировки объекта, в течение и после которой сохраняются значения показателей безотказности, долговечности и ремонтопригодности в установленных пpeделах.

Номенклатура показателей сохраняемости включает в себя два единичных показателя: средний срок сохраняемости и гамма-процентный срок сохраняемости.

1) Средний срок сохраняемости - математическое ожидание срока сохраняемости объекта. Его определяют по уравнению: 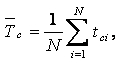где   - срок сохраняемости i - го объекта. Обычно средний срок сохраняемости задается таким образом, чтобы в течении хранения и транспортирования машин уменьшение их наработки до отказа не превышало 10…15 %. Например, для аккумуляторов средний срок сохраняемости составляет 2…3 года, для двигателей – 2 года.

 

2) Гамма-процентный срок сохраняемости – срок сохраняемости, достигаемый объектом с заданной вероятносгью, выраженной в процентах. Гамма-процентный  срок  сохраняемости  определяют аналогично гамма-процентному ресурсу или сроку службы по интегральной кривой вероятности  безотказной работы или же по аналитическим уравнениям в зависимости от закона распределения срока сохраняемости совокупности объектов: - при законе нормального распределения:

- при законе распределения Вейбулла:

44. Комплексные показатели надежности. Вероятностные и статистические методы определения показателей. Коэффициент готовности. Процесс функционирования восстанавливаемого объекта можно представить как последовательность чередующихся интервалов работоспособности и восстановления (простоя).

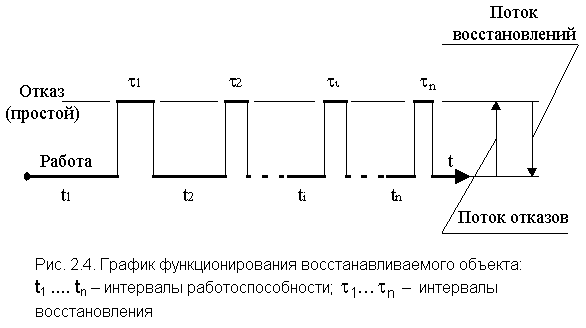
Коэффициент готовности - это вероятность того, что объект окажется в работоспособном состоянии в произвольный момент времени, кроме планируемых периодов, в течение которых применение объекта по назначению не предусматривается. Этот показатель одновременно оценивает свойства работоспособности и ремонтопригодности объекта.

Для одного ремонтируемого объекта коэффициент готовности 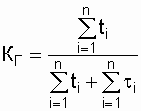(2.22) ; 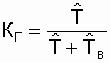 , КГmax = 1. Из выражения видно, что коэффициент готовности объекта может быть повышен за счет увеличения наработки на отказ и уменьшения среднего времени восстановления. Для определения коэффициента готовности необходим достаточно длительный календарный срок функционирования объекта.

Зависимость коэффициента готовности от времени восстановления затрудняет оценку надежности объекта, так как по КГ нельзя судить о времени непрерывной работы до отказа. К примеру, для одного и того же численного значения КГ можно иметь малые интервалы  и ti (см. рис. 2.4) и значительно большие. Таким образом можно доказать, что на конкретном интервале работоспособности вероятность безотказной работы будет больше там, где больше ti, хотя за этим интервалом может последовать длительный интервал простоя  . Коэффициент готовности является удобной характеристикой для объектов, которые предназначены для длительного функционирования, а решают поставленную задачу в течение короткого промежутка времени (находятся в ждущем режиме), например, релейная защита, контактная сеть (особенно при относительно малых размерах движения), сложная контрольная аппаратура и т.д.

Коэффициент оперативной готовности. Коэффициент оперативной готовности КОГопределяется как вероятность того, что объект окажется в работоспособном состоянии в произвольный момент времени (кроме планируемых периодов, в течение которых применение объекта по назначению не предусматривается) и, начиная с этого момента, будет работать безотказно в течение заданного интервала времени.

Из вероятностного определения следует, что , (2.23)

где КГ - коэффициент готовности; Р(tр) - вероятность безотказной работы объекта в течение времени (tр), необходимого для безотказного использования по назначению.

Для часто используемого в расчетной практике простейшего потока отказов, когда

l = w ,Р(tр) соответственно определяется по выражению .

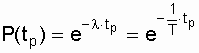Коэффициент технического использования. Коэффициент технического использования КТИравен отношению математического ожидания суммарного времени пребывания объекта в работоспособном состоянии за некоторый период эксплуатации к математическому ожиданию суммарного времени пребывания объекта в работоспособном состоянии и простоев, обусловленных техническим обслуживанием и ремонтом за тот же период эксплуатации: 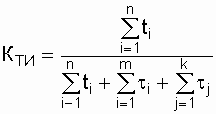, (2.25)

где ti - время сохранения работоспособности в i-м цикле функционирования объекта;  - время восстановления (ремонта) после i-го отказа объекта;  - длительность выполнения j-й профилактики, требующей вывода объекта из работающего состояния (использования по назначению); n - число рабочих циклов за рассматриваемый период эксплуатации; m - число отказов (восстановлений) за рассматриваемый период; k - число профилактик, требующих отключения объекта в рассматриваемый период.

Как видно из выражения (2.25), коэффициент технического использования характеризует долю времени нахождения объекта в работоспособном состоянии относительно общей (календарной) продолжительности эксплуатации. Следовательно, КТИотличается от КГтем, что при его определении учитывается все время вынужденных простоев, тогда как при определении КГвремя простоя, связанное с проведением профилактических работ, не учитывается.

Суммарное время вынужденного простоя объекта обычно включает время:

- на поиск и устранение отказа;

- на регулировку и настройку объекта после устранения отказа;

- для простоя из-за отсутствия запасных элементов;

- для профилактических работ.

В электроэнергетических объектах, к примеру, в трансформаторах, линиях электропередачи, шинах распределительных устройств и т.п., предусмотрены плановые отключения для проведения плановых ремонтов и технического обслуживания. Эти интервалы времени так же как и интервалы, связанные с отключением по причине отказа, учитываются при определении анализируемых коэффициентов надежности.

45. Интервальная оценка вероятности безотказной работы и вероятности отказа по частоте отказов при условии ее нормального распределения.

2.1.1. Доверительный интервал для оценки математического ожидания при известном s.

Пусть количественный признак генеральной совокупности распределен нормально. Известно среднее квадратическое отклонение  этого распределения -s. Требуется оценить математическое ожидание а по выборочной средней. Найдем доверительный интервал, покрывающий а с надежностью g. Выборочную среднюю будем рассматривать как случайную величину ( она изменяется от выборки  к выборке), выборочные значения признака- как одинаково распределенные независимые СВ с математическим ожиданием каждой а и средним квадратическим отклонением s. Примем без доказательства, что если величина Х распределена нормально, то и выборочная средняя тоже распределена нормально с параметрами  .

Потребуем, чтобы выполнялось равенство   

Заменив Х и s, получим   

Получим

Задача решена.  Число t находят по таблице функции Лапласа Ф(х).

2.1.2. Доверительный интервал для оценки математического ожидания при неизвестном s.

Т.к. мы не знакомы с законами распределения СВ, которые используются при выводе формулы, то примем ее без доказательства.

В качестве неизвестного параметра s используют исправленную дисперсию s2 . Заменяя s на s, t на величину tg. Значение  этой величины зависит от надежности g и объема выборки n  и определяется  по " Таблице значений tg."  Итак : и доверительный интервал имеет вид

2.1.3. Доверительный интервал для оценки дисперсии и среднего квадратического отклонения.

Требуется оценить неизвестную генеральную дисперсию и генеральное среднее квадратическое отклонение по исправленной дисперсии, т.е. найти доверительные интервалы, покрывающие параметры D и s с заданной надежностью g.

Потребуем выполнения соотношения  .

Раскроем модуль и получим двойное неравенство:  .

Преобразуем:  . Обозначим d/s = q (величина q находится по  "Таблице значений q"и зависит от надежности и объема выборки), тогда доверительный интервал для оценки генерального среднего квадратического отклонения имеет вид:

 . Замечание : Так как s >0, то если q >1 , левая граница интервала равна 0:          0< s < s ( 1 + q ).