1.Общие понятия теории надежности. Надёжность – свойство изделия выполнять заданные функции, сохраняя свои эксплуатационные показатели в заданном интервале времени, в течение заданной наработки. Теория надёжности – наука, которая изучает закономерности влияния отказов на эффективности использования аппаратуры. Безотказность - свойство объекта непрерывно сохранять работоспособное состояние в течение некоторого времени или наработки. Долговечность - свойство объекта сохранять работоспособное состояние до наступления предельного состояния при установленной системе технического обслуживания и ремонта. Ремонтопригодность – это свойство объекта, заключающееся в приспособленности к поддержанию и восстановлению работоспособного состояния путем технического обслуживания и ремонта. Сохраняемость – свойство объекта сохранять в заданных пределах значения параметров, характеризующих способности объекта выполнять требуемые функции, в течение и после хранения и (или) транспортирования.

2. Состояния объектов. Работоспособное - состояние, при котором значение параметров характеризует способность системы объекта выполнить заданные функции находятся в пределах установленных нормат. техн. документацией. Неработоспособное - при котором значения хотя бы одного параметра не находятся в пределах устан. Исправное - при котором объект полностью соотв-ет требованиям нормат. техн. или конструкт-ой документации. Неисправное - когда имеется хотя бы одно несоответствие докум. Предельное состояние - состояние объекта, при котором его дальнейшая эксплуатация недопустима или нецелесообразна, либо восстановление его работоспособного состояния невозможно или нецелесообразно. Критерий предельного состояния (кпс) - признак или совокупность признаков предельного состояния объекта, установленные нормативно-технической и (или) конструкторской (проектной) документацией.

3. Классификация отказов. Отказ – событие, заключающееся в нарушении работоспособности. Критерий отказа - признак или совокупность признаков нарушения работоспособного состояния объекта, установленные в нормативно-технической и (или) конструкторской (проектной) документации. а) В зависимости от характера изменения параметров объекта до момента наступления отказа: внезапные (резкое скачкообразное изменение параметров), постепенные (наступает в результате длительного изменения парам-ов) б) По степени нарушения работоспособности отказы делятся на полные и частичные. Полные -объект не функционирует полностью. Частичный – объект продолжает функ-ть с ухудшенными показателями. в) По хар-ру внешнего проявления делятся на явные и неявные: явные отказы-обнаруживаются непосредственно после возникн-ия. Неявные-необнаруженные после возникновения. Метрологич. отказ выр-ся в выходе за пределы систематич. и случ. погрешности измерения. г) В связи с предшествующими отказами: первичные (независимые), вторичные (зависимые) не являются следствием ранее возникших отказов. д) по длительности действия: Устойчивый отказ-систематический отказ требующий ремонт устройства. Неустойчивый отказ-сбой-(по ГОСТ 19542-83) кратковременное нарушение правильной работы ВУ, после которого работосп-ть ВУ самовосстанавливается или восст-ся оператором без ремонта. е)Аппаратные-событие приводящее к утрате работоспособности при этом для восстановления требуется замена аппаратуры. Программные-события, когда объект утрачивает работосп-ть по причине несовершенства ПО.

4. Техническое обслуживание и ремонт. Техническое обслуживание - комплекс технических и организационных мероприятий, осуществляемых в процессе эксплуатации технических объектов с целью обеспечения требуемой эффективности выполнения ими заданных функций. Восстановление - событие-переход объекта в работоспособное состояние. Ремонт - замена неисправных элементов, устранение изъянов. Обслуживаемый объект - объект, для которого проведение технического обслуживания предусмотрено нормативно-технической, конструкторской или проектной документацией. Необслуживаемый объект - объект, для которого проведение технического обслуживания не предусмотрено нормативно-технической, конструкторской или проектной документацией. Восстанавливаемый объект — это объект, работоспособность которого в случае возникновения отказа подлежит восстановлению в рассматриваемой ситуации. Невосстанавливаемый объект — это объект, работоспособность которого в случае возникновения отказа не подлежит восстановлению в рассматриваемой ситуации. Ремонтируемый объект — это объект, исправность и работоспособность которого в случае возникновения отказа или повреждения подлежит восстановлению. Неремонтируемый объект — это объект, исправность и работоспособность которого в случае возникновения отказа или повреждения не подлежит восстановлению.

5. Временные понятия теории надёжности. Наработка– продолжительность или объем работы объекта. Наработка до отказа— наработка объекта от начала эксплуатации до возникновения первого отказа. Наработка между отказами — это наработка объекта от окончания восстановления его работоспособного состояния после отказа до возникновения следующего отказа. Время восстановления - это время, затраченное на обнаружение, поиск причины отказа и устранения последствий отказа. Ресурс – это суммарная наработка объекта от начала его эксплуатации или ее возобновления после ремонта до перехода в предельное состояние. Срок службы - календарная продолжительность эксплуатации от начала эксплуатации объекта или ее возобновления после ремонта до перехода в предельное состояние. Срок сохраняемости - календарная продолжительность хранения или транспортирования объекта, в течение которой сохраняются в заданных пределах значения параметров, характеризующих способность объекта выполнять заданные функции. Назначенный ресурс – суммарная наработка, при достижении которой эксплуатация объекта должна быть прекращена независимо от его технического состояния. Назначенный срок службы – календарная продолжительность эксплуатации объекта, при достижении которой применение по назначению должно быть прекращено. Назначенный срок хранения — календарная продолжительность хранения, при достижении которой хранение объекта должно быть прекращено независимо от его технического состояния. 

6,7,8. Причины изменения технического состояния и отказов механических систем. Причинами процесса нарушения функционирования МС являются нарушения и несовершенства конструирования, изготовления и эксплуатации МС: 1) в процессе конструирования:  несоответствие материала назначению объекта;  отсутствие или несоответствие испытаний материала;  несоответствие расчетов объекта нормативно-технической документации;  отсутствие или несоответствие испытаний объекта; 2) в процессе изготовления:  несоответствие материала техническим требованиям;  несоответствие объекта техническим требованиям;  несоответствие сборки и регулировки объекта; 3) в процессе эксплуатации:  несоответствие периодичности, объемов и качества технического обслуживания и ремонта условиям эксплуатации;

 несоответствие рабочих параметров и воздействующих факторов нормативно-технической документации;  несоответствие сборки и регулировки объекта. Факторы:  конструктивно технологический ( дефекты конструкции), качество материалов, совершенство технологии работ, качество и сортность эксплуатационных материалов. Изнашивание — это процесс постепенного изменения размеров и формы тела при трении, проявляющийся в отделении с поверхности трения материала и в его остаточной деформации. Пластическая деформация - деформация, которая не исчезает после того, как снята нагрузка. Пластическое разрушение – разрушение, которое происходит после существенной пластической деформации, протекающей по всему или почти по всему объему тела. Коррозия - это самопроизвольное разрушение металлов под воздействием химического или физико-химического влияния  окружающей  среды. 

9. Общие понятия теории вероятностей. Теория вероятностей – математическая наука, изучающая закономерности в случайных явлениях. Одним из основных понятий теории вероятностей является понятие случайного события (или просто события). Событие - любой факт, который в результате опыта может произойти или не произойти. Достоверное - событие, которое происходит в каждом опыте. Невозможное - событие , которое в результате опыта произойти не может. Несовместное - событие, которое в одном опыте не могут произойти одновременно. Сумма (объединение) двух событий A и B - такое событие, которое заключается в том, что происходит хотя бы одно из событий, т.е. A или B, или оба одновременно. Произведение (пересечение) двух событий A и B - такое событие, которое заключается в том, что происходят оба события A и B вместе.

10. Вероятность события и частота события. Частота события А - отношение числа m наступлений данного случайного события A в данной серии испытаний к общему числу n испытаний этой серии и обозначается Р*(А). Таким образом, P*(A)=m/n.  Частота случайного события всегда заключена между нулем и единицей: 0 ≤ P*(A) ≤ 1. Вероятность события А - отношение числа исходов опыта, благоприятных этому событию, к числу возможных исходов. Вероятность случайного события, как и его частота, заключена между нулем и единицей: 0 ≤ P(A) ≤ 1. Достоверному событию (т.е. событию, которое должно произойти при каждом испытании) приписывают вероятность Р(А)=1. Невозможному событию (т.е. событие, которое не может произойти ни при одном испытании) приписывают вероятность Р(А)=0.

11. Вероятность определенного сочетания элементов различных типов в выборке. Есть генеральная совокупность N элементов, среди которых N₁ – 1 элемента и т.д. (N=М₁+…+М_к). Берем n элементов. Найдем m₁ 1 элемента (n=m₁+…+m_k). P_{m1,m2….mn; n}=C_M1^m1*…* C_Mn^mn /C_Nⁿ. Частный случай (общая постановка задач): Р_m,n= C_M^m*…* C_N-M^n-m /C_Nⁿ.

12. Вероятность совместного появления события. Произведением событий A и B называется событие, при котором произошло и A, и B, обозначается оно AB. Независимыми называются события A и B, если вероятность события A не зависит от того, наступило событие B или нет. Вероятность произведения независимых событий равна произведению соответствующих вероятностей (p(AiAk) = p(Ai) p(Ak)). Если вероятность наступления события A зависит от того, наступило событие B или нет, события называют зависимыми и вводят понятие условной вероятности. Условной вероятностью события A при условии того, что произошло событие B, называют величину p(A|B)= p(AB)/p(B). Соответственно, для зависимых событий p(AB) = p(B) p(A|B).

13. Вероятность появления одного из несовместных событий. Суммой А + В двух событий А и В называют событие, состоящее в появлении события А, или события В, или обоих этих событий. Вероятность появления одного из двух несовместных событий, безразлично какого, равна сумме вероятностей этих событий: Р(А+В)=Р(А)+Р(В). Несколько событий образуют полную группу, если в результате испытания появится хотя бы одно из них. Сумма вероятностей попарно несовместных событий А₁, А₂, …, А_n, образующих полную группу, равна единице: Р(А₁)+Р(А₂)+…+Р(А_n)=1. Сумма вероятностей противоположных событий равны единице: Р(А)+Р(Ā)=1.

14. Вероятность появления хотя бы одного из совместных событий. Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления: Р(А+В)=Р(А)+Р(В) - Р(АВ). Вероятность появления хотя бы одного из событий А_1, А₂, …, А_n, независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий  Ā₁, Ā₂, …, Ā_n: Р(А₁+А₂+…+А_n)=1- Р(Ā₁)*Р(Ā₂)*…*Р(Ā_n).

15. Формула полной вероятности. Если известно, что событие A может произойти вместе с одним из событий H₁,H₂,H_n (гипотез), образующими полную группу попарно несовместных событий, то событие A можно представить как объединение событий AH₁,AH₂,AH_n, т. е. A=AH₁,AH₂,AH_n. Вероятность события А можно определить по формуле P(A)=P(H₁)*P(A/H₁)+P(H₂)*P(A/H₂)+…+P(H_n)*P(A/H_n)

или P(A)= ∑_i=1ⁿ P(H_i) P(A/H_i). 

16. Формула Байеса. Пусть имеется полная группа попарно несовместных событий H_i I ϵ 1,n  с известными вероятностями P(H_i). Достоверное событие Ὠ является их объединением: Ὠ =∑H_i, ∑P(H_i)=1. Рассматривается событие A, для которого известно n условных вероятностей P(A/H_i). Требуется найти вероятность P(H_i/A)=? По определению условной вероятности получаем: P(H_i/A)= P(AH_i)/P(A)= P(A/H_i)* P(H_i)/P(A) = P(A/H_i)* P(H_i)/ ∑P(A/H_k)*P(H_k), где для вероятности события A использована формула полной вероятности: P(A)= ∑P(A/H_k)*P(H_k) Если сложить все P(H_i/A), то получится единица, поэтому множитель 1/P(A), не зависящий от H_i, можно считать константой, которую можно найти в самом конце из условия нормировки.

17. Формула Бернулли. Пусть производится n независимых испытаний. Ставится задача определения вероятности того, что ровно в m испытаниях наступит событие A, если вероятность наступления этого события в каждом испытании равна p. Определим вначале вероятность того, что в первых m испытаниях событие A наступит, а в остальных n-m  испытаниях — не наступит. Вероятность такого события может быть получена на основании формулы вероятности произведения независимых событий P=p^m*q^n-m,

где q=1-p. Так как рассматривалась только одна из возможных комбинаций, когда событие A произошло только в первых m испытаниях, то для определения искомой вероятности нужно перебрать все возможные комбинации. Их число будет равно числу сочетаний из n элементов по m, т.е. C_n^m. Таким образом, вероятность того, что событие A наступит ровно в m испытаниях определяется по формуле P_n(m)= C_n^m* p^m*q^n-m, где C_n^m=n!/(n-m)!m!.

18. Распределение дискретных случайных величин. Вероятностное и статистическое выражение законов распределения. Случайная величина - величина, принимающая в зависимости от случая те или иные значения с определёнными вероятностями. В зависимости от типа множества, на котором сосредоточена вся единичная вероятностная масса, распределения делят на дискретные, абсолютно непрерывные, сингулярные и их смеси. Дискретной называют случайную величину, значения которой изменяются не плавно, а скачками, т.е. могут принимать только некоторые заранее определённые значения. Закон распределения ДСВ представляет собой перечень всех её возможных значений и соответствующих вероятностей. Сумма всех вероятностей Σp_i =1. Функция распределения случайной величины - это вероятность того, что случайная величина (ξ) примет значение меньшее, чем конкретное числовое значение x: F(X) = P(ξ < X). Для ДСВ функция распределения вычисляется для каждого значения как сумма вероятностей, соответствующих всем предшествующим значениям случайной величины. 

Таблица соответствия значений СВ и их вероятностей называется рядом распределения

Xi	X1	X2	…	Xk
Pi	P1	P2	…	Pk

Графическое представление этой табл наз-ся многоугольником распределения.  При этом сумма всех ординат многоугольника распределения предст-т собой в\ть всех возможных значений сл\в, а, след, =1. Следствие: Из определения закона распределения следует что события (Х=х),…, (Х=хк) –образуют полн. систему. => Р(Х=х1)+…+Р(Х=хк)=1 основное св-во закона распределения. Свойства функции распределения: 1) ФР сл\в есть неотрицательная ф-я, заключенная м\у 0 и 1:

2) ФР сл\в есть неубывающая ф-я на всей числовой оси.  при

3) На минус бесконечности ФР = нулю, на плюс бесконечности ФР = единице.

; 4) Вер-ть попадания сл\в в интервал (включая ) равна приращению её ФР на этом интервале, т.е.

19. Распределение непрерывных случайных величин. Вероятностное и статистическое выражение законов распределения. Сл\в Х наз-ся непрерывной, если её Функция Распределения непрерывна в любой точке и дифференцируемая во всюду, кроме отдельных точек (точки излома). Функция распределения НСВ: , в качестве способа задания НСВ используется функция распределения НСВ. ФРНСВ наз вер-ть т\ч она примет значение меньшее заданного. -обознач ф-ии распр в-тей  Основные свойства ф-ии распределения НСВ: С1. С2. С3. С4. Вер-ть т\ч НСВ примет значение из интервала, равна приращению ф-ии на этом интервале 1) 2) Скорость изменения функции распределения хар-ся плотностью распр-я. Обозначается символом . Плотностью вер-ти (плотностью распр-я) НСВ Х наз-ся производная её ф-ии распр-я

Свойства плотности распр-я (ПР): С1. ПР – неотрицательная функция. ; С2. Вер-ть попадания НСВ в интервал [a,b] равна определённому интегралу от её плотности вер-ти в пределах от a до b, т.е. С3. Ф-я распр НСВ м\б выражена через плотность вер-ти по формуле: С4. Несобственный интеграл в бесконечных пределах от плотности вер-ти НСВ =1.

20. Числовые характеристики ДСВ и НСВ. Вероятностные и статистические методы определения числовых характеристик. Матем ожиданием дискретной сл\в наз сумма произведений всех возможных значений сл\в на их вероятности. Свойства математического ожидания:

1) Мат ожид постоянной величины равно самой постоянной.

2) Постоянный множитель можно выносить за знак мат-го ожид.

3) Мат ожид произведения 2х независ-х сл\в-н = произведению их матем-х ож-й. Это свойство справедливо для произвольного числа сл\в.

4) Мат ожид суммы 2х сл\в = сумме мат ожид-й слагаемых.

Дисперсией (рассеиванием) дискретной сл\в наз мат ожид квадрата отклонения сл\в от ее мат ожид. Свойства дисперсии: С1. Дисперсия постоянной величины равна нулю. С2. Постоян множитель можно выносить за знак дисперсии, возводя его в квадрат. С3.Дисперсия суммы 2х независимых сл\в = сумме дисперсий этих величин.

С4. Дисперсия разности 2х независимых сл\в = сумме дисперсий этих величин. С5. Дисперсия = мат ожид квадрата сл\в без квадрата мат ожид. Мат\ож-м  НСВ Х, возможные значения которой принадлежат отрезку [a,b], наз-ся определенный интеграл . Если возможные значения сл\в рассм-ся на всей числовой оси, то мат\о нах по формуле: , при этом предпол-ся, что несобственный интеграл сходится. Дисперсией НСВ наз мат\ож квадрата ее отклонения. . По аналогии с дисперсией, дискретной сл\в, для практического вычисления дисперсии используется формула: . Среднее квадратическое отклонение дискретной случайной величины, оно же стандартное отклонение или среднее квадратичное отклонение есть корень квадратный из дисперсии: σ(X) = √D(X)

Мода дискретной случайной величины Mo(X) - это значение случайной величины, имеющее наибольшую вероятность. На многоугольнике распределения мода - это абсцисса самой высокой точки. Бывает, что распределение имеет не одну моду.

Коэффициент вариации случайной величины - это относительная мера вариации. V(X) = |σ(X)/M(X)| · 100% Среднее квадратическое отклонение непрерывной случайной величины, оно же стандартное отклонение или среднее квадратичное отклонение есть корень квадратный из дисперсии: σ(X) = √D(X)

Мода непрерывной случайной величины Mo(X) - значение с.в., имеющее наибольшую вероятность. Если в задаче требуется определить моду - находим экстремум (максимум) плотности вероятности f(x).

Коэффициент вариации непрерывной случайной величины вычисляется по той же формуле, что и для дискретной с.в.:

21. Моменты СВ. Вероятностные и статистические методы их определения. В теории вероятностей и математической статистике, помимо математического ожидания и дисперсии, используются и другие числовые характеристики случайных величин. В первую очередь это начальные и центральные моменты.

Начальным моментом k-го порядка случайной величины x называется математическое ожидание k-й степени случайной величины x , т.е. a k = Mx k.

Центральным моментом k-го порядка случайной величины x называется величина m k, определяемая формулой m k = M(x - Mx )k.

Заметим, что математическое ожидание случайной величины - начальный момент первого порядка, a ₁ = Mx , а дисперсия - центральный момент второго порядка,

a ₂ = Mx ² = M(x - Mx )² = Dx .

Существуют формулы, позволяющие выразить центральные моменты случайной величины через ее начальные моменты, например:

m ₂=a ₂-a ₁², m ₃ = a ₃ - 3a _2a 1 + 2a ₁³.

Если плотность распределения вероятностей непрерывной случайной величины симметрична относительно прямой x = Mx , то все ее центральные моменты нечетного порядка равны нулю.

22. Точечные и интервальные оценки вероятностных величин. Свойства точечных оценок. ТОЧЕЧНАЯ ОЦЕНКА - оценка, имеющая конкретное числовое значение. Например, среднее арифметическое: X = (x1+x2+...+xn)/n, где: X - среднее арифметическое (точечная оценка МО);    x1,x2,...xn - выборочные значения; n - объем выборки.  ИНТЕРВАЛЬНАЯ ОЦЕНКА - оценка представляемая интервалом значений, внутри которого с задаваемой исследователем вероятностью находится истинное значение оцениваемого параметра. Интервал в интервальной оценке называется  ДОВЕРИТЕЛЬНЫМ ИНТЕРВАЛОМ, задаваемая исследователем вероятность называется ДОВЕРИТЕЛЬНОЙ ВЕРОЯТНОСТЬЮ. В практике статистических вычислений применяются стандартные значения доверительной вероятности: 0,95, 0,98 и 0,99 (95%, 98% и 99% соответственно).  Очевидно, что чем выше доверительная вероятность, тем выше точность оценки, но шире доверительный интервал. Отсюда следует – ДЛЯ НСВ ВЕРОЯТНОСТЬ ТОГО, ЧТО ТОЧЕЧНАЯ ОЦЕНКА (ширина доверительного интервала равна 0) СОВПАДЕТ С ЛЮБЫМ ЗАДАННЫМ ЗНАЧЕНИЕМ ИЛИ ОЦЕНИВАЕМЫМ ПАРАМЕТРОМ РАВНА 0.  Таким образом, точечная оценка имеет смысл лишь тогда, когда приведена характеристика рассеяния этой оценки (дисперсия). В противном случае она может служить лишь в качестве исходных данных для построения интервальной оценки.

Для того чтобы оценка   имела практическую ценность, она должна обладать следующими свойствами. 1. Оценка   параметра q называется несмещенной, если ее математическое ожидание равно оцениваемому параметру  q , т.е.

                                                М  =  q .                                                   Если равенство не выполняется, то оценка   может либо завышать значение q  (М  > q ), либо занижать его (М  <  q ) .   2. Оценка    параметра q называется состоятельной , если она подчиняется закону больших чисел, т.е. сходится по вероятности к оцениваемому параметру при неограниченном возрастании числа опытов (наблюдений ) и, следовательно, выполняется следующее равенство:    где e > 0 сколько угодно малое число. Для выполнения достаточно, чтобы дисперсия оценки стремилась к нулю при  , т.е.   и кроме того, чтобы оценка была несмещенной.          Итак, состоятельность оценки означает, что при достаточно большом количестве опытов и со сколько угодно большой  достоверностью отклонение оценки от истинного значения параметра меньше любой наперед заданной величины. 3. Несмещенная оценка  , которая имеет наименьшую  дисперсию среди всех возможных несмещенных оценок параметра q, вычисленных по выборкам одного и того же объема , называется эффективной оценкой.

23. Точечные и интервальные оценки вероятностных величин. Интервальная оценка математического ожидания СВ.    Точечная оценка не позволяет определить, с какой вероятностью полученная величина оценки соответствуют истинному значению характеристики генеральной совокупности. Чтобы ответить на этот вопрос вводят понятие интервальной оценки. Пусть  - истинное среднее генеральной совокупности,    - точечная оценка  , полученная по формуле. Введем доверительный интервал  (2.15) где   - некоторое произвольное число, назначенное исследователем. Введем также доверительную вероятность   как вероятность того, что истинное значение среднего   попадет в записанный выше доверительный интервал, т.е.  (2.16). Чтобы вычислить   перейдем от абсолютных величин   и   к ошибкам в определении среднего   для чего вычтем   из всех частей неравенства (2.16). В результате получим (2.17) Подставим в последнее соотношение   и с учетом того, что величина выборочного среднего   распределена по нормальному закону   ,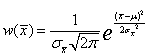

  (2.18) Отсюда    (2.19) Здесь 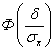  - интеграл вероятности, который имеет вид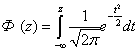 (2.20) Обозначим    вероятность того, что истинное значение   выйдет за пределы доверительного интервала. Эта  вероятность называется уровнем значимости. Поскольку выход за пределы доверительного интервала возможен как справа, так и слева от его границ с одинаковой вероятностью, равной  , из (2.19) следует соотношение (2.21) Обозначим   - квантиль уровня   стандартного гауссовского распределения (распределение, для которого среднее значение равно нулю, дисперсия – единице). По определению  квантиль  удовлетворяет уравнению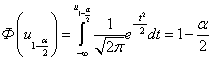  (2.22)Из (2.21) и (2.22) следует (2.23)Отсюда  (2.24) Подставив (2.24)  в  (2.16), получим выражение для доверительного интервала   (2.25)

Или   (2.26) Здесь   -  среднеквадратическое значение одиночного измерения. Последнее соотношение в соответствии с ГОСТ Р 50779.21 – 96 называется интервальной оценкой генеральной средней, полученной по гауссовской выборке объема n для случая известной дисперсии. Физический смысл этой оценки поясним следующим примером. Зададим уровень значимости  . Отсюда следует  = 3. В результате образуется доверительный интервал шириной  , куда величина неизвестного генерального среднего  входит с вероятностью 1-0.0027=0.997.

24. Точечные и интервальные оценки вероятностных величин. Интервальная оценка вероятности события.  "Хорошей" точечной оценкой вероятности  р  события  А является частость  , где n - общее число испытаний, а событие А может произойти с вероятностью р или не произойти с вероятностью q=1-p (последовательность испытаний Бернулли). Интервальная оценка для р задается в виде P(p1<p<p2)=1-α,

где (p1, p2) - границы интервала для вероятности р, отвечающие надежности 1-α, α уровень значимости. Интервальная оценка зависит от объема выборки n.

25. Равномерное дискретное распределение случайной величины. Параметры и числовые характеристики равномерного дискретного распределения.

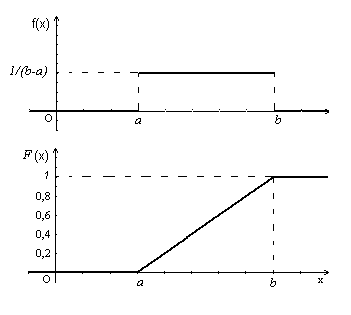
Плотность вероятности равномерного распределения сохраняет на интервале (a, b) постоянное значение, вне этого интервала плотность вероятности равна нулю. Исходя из основного свойства плотности вероятности, f(x) = 1/(b-a) на интервале (a;b). Интегральную функцию распределения (вероятность того, что с.в. примет значение меньшее, чем x) находим как интеграл от -∞ до x от плотности вероятности: F(x) = (x-a)/(b-a). Графики плотности вероятности и функции равномерного распределения:

Математическое ожидание равномерного распределения: M(X) = (a + b)/2. Дисперсия равномерного распределения: D(X) = (b - a)2/12.Среднее квадратичное отклонение равномерного распределения: σ(X) = (b - a)/(2√3)

26. Гипергеометрическое распределение случайной величины. Параметры и числовые характеристики гипергеометрического распределения. Имеется N объектов. Из них n объектов обладают требуемым свойством. Из общего количества отбирается m объектов. Случайная величина X - число объектов из m отобранных, обладающих требуемым свойством. Для вычисления вероятностей используются биномиальные коэффициенты (см. число сочетаний). Закон распределения имеет вид:

27. Геометрическое распределение случайной величины. Параметры и числовые характеристики геометрического распределения. Производится серия испытаний. Случайная величина - количество испытаний до появления первого успеха (например, бросание мяча в корзину до первого попадания). Закон распределения имеет вид:

Если количество испытаний не ограничено, т.е. если случайная величинв может принимать значения 1, 2, ..., ∞, то математическое ожидание и дисперсию геометрического распределения можно найти по формулам M(X) = 1/p, D(X) = q/p2

28. Биномиальное распределение случайной величины. Параметры и числовые характеристики биномиального распределения. Биномиальным называют закон распределения дискретной случайной величины X - числа появлений события в n независимых испытаниях, в каждом из которых вероятность наступления события постоянна. Вероятности pi вычисляют по формуле Бернулли

Для биномиального распределения:математическое ожидание M(X) = np, дисперсия D(X) = npq, мода np-q ≤ Mo ≤ np+p, коэффициент асимметрии As = (q - p)/√npq, коэффициент эксцесса Ex = (1 - 6pq)/npq. В пределе при n→∞ биномиальное распределение по своим значениям приближается к нормальному с параметрами a=np и σ=√npq. В пределе при n→∞ и при p→0 биномиальное распределение превращается в распределение Пуассона с параметром λ=np.

29. Распределение Пуассона. Параметры и числовые характеристики распределения Пуассона. Пусть имеется некоторая последовательность событий, наступающих в случайные моменты времени (будем называть это потоком событий).  Интенсивностьпотока (среднее число событий, появляющихся в единицу времени) равна λ. Пусть этот поток событий - простейший (пуассоновский), т.е. обладает тремя свойствами: 1) вероятность появления k событий за определённый промежуток времени зависит только от длины этого промежутка, но не от точки отсчёта, другими словами, интенсивность потока есть постоянная величина (свойство стационарности); 2) вероятность появления k событий в любом промежутке времени не зависит от того, появлялись события в прошлом или нет (свойство «отсутствия последействия»); 3) появление более одного события за малый промежуток времени практически невозможно (свойство ординарности). Вероятность того, что за промежуток времени t событие произойдёт k раз, равна

30. Потоки событий и их основные характеристики. Распределение времени между событиями в потоке. Простейший поток событий и его особенности. Простейшим видом СП являются потоки событий. Потоком событий называется некоторая последовательность однотипных событий, которые происходят в случайные моменты времени (например, звонки по телефону, посетители магазина, автомобили, проезжающие перекресток и т.д.). Они относятся к СП с дискретным состоянием и непрерывным временем. Математически поток событий можно изобразить в виде случайных точек на оси времени.            Если события в потоке происходят поодиночке, а не группами из нескольких событий, то такой поток называется ординарным. Поток событий называется потоком без последствий, если для любых непересекающихся интервалов времени style='color:red'> число событий в одном интервале никак не влияет на то, сколько и каким образом будут происходить события в другом интервале. Ординарный поток без последствия называется потоком Пуассона. Важнейшей характеристикой любого потока событий является его интенсивность – среднее число событий, произошедших в потоке за одну единицу времени  .       С интенсивностью тесно связана величина  , которая имеет смысл среднего интервала времени между двумя событиями. Если интервалы между соседними событиями есть случайные величины, которые независимы друг от друга, то такой поток событий называется потоком Пальма.      Если интенсивность потока событий не зависит от времени  , то такой поток называется стационарным. Если в потоке события происходят через равные интервалы времени, то он называется регулярным.      Стационарный поток Пуассона называется простейшим потоком. В экономическом моделировании в основном используют потоки Пуассона, в том числе простейшие. Для них справедливы следующие теоремы:      1) Число событий, произошедших в потоке Пуассона, есть случайная величина, распределённая по закону Пуассона. Вероятность того, что в потоке Пуассона с интенсивностью   за интервал времени (t1; t2) произойдёт ровно k событий, равна: 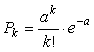        , где 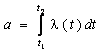  .      Если поток простейший  , то  .      2) Интервал между событиями или время ожидания очередного события T в потоке Пуассона есть случайная величина, распределенная по показательному закону, т. е вероятность того, что следующее событие произойдет не ранее t, равна:       .

31. Нормальное распределение случайной величины. Параметры и числовые характеристики нормального распределения. Нормальное распределение имеет плотность вероятности 1/[σ√2π]·e-(x-a)2/2σ2, где a - математическое ожидание, σ - среднее квадратическое отклонение. 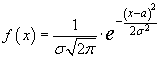Значения плотности нормального распределения для конкретного числового значения x можно вычислить в Excel с помощью формулы =НОРМРАСП(x;a;σ;0). Если a = 0, σ = 1, то такое нормальное распределение называется стандартным. Значения плотности стандартного нормального распределения можно посмотреть в таблице или вычислить в Excel с помощью формулы =НОРМРАСП(x;0; 1;0) График нормального распределения имеет куполообразную форму, он симметричен относительно своего математического ожидания, а на степень его островершинности влияет величина среднего квадратичного отклонения σ.

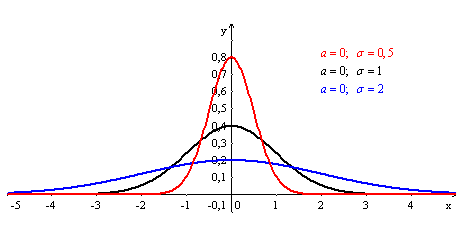
Асимметрия, эксцесс, мода и медиана нормального распределения равны: As(X) = 0; Ex(X) = 0; Mo(X) = a; Me(X) = a, где а - математическое ожидание. Интегральная функция нормального распределения вероятностей: 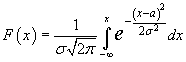Интегральная функция распределения вероятностей показывает вероятность того, что с.в. примет значение меньшее, чем x: F(x) = P(ξ < x). Численно она равна площади криволинейной трапеции, ограниченной сверху графиком плотности вероятности, снизу осью OX, на интервале от -∞ до x. Ниже дана иллюстрация.

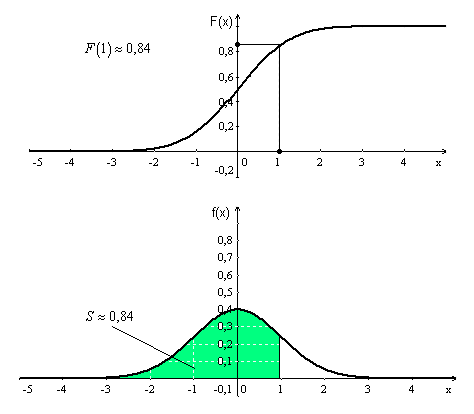
32. Равномерное непрерывное распределение случайной величины. Параметры и числовые характеристики равномерного непрерывного распределения. Непрерывная случайная величина Х имеет равномерное распределение на отрезке [а, в], если на этом отрезке плотность распределения вероятности случайной величины постоянна, т. е. если дифференциальная функция распределенияf(х) имеет следующий вид: Иногда это распределение называют законом равномерной плотности. Про величину, которая имеет равномерное распределение на некотором отрезке, будем говорить, что она распределена равномерно на этом отрезке.

Найдем значение постоянной с. Так как площадь, ограниченная кривой распределения и осью Ох, равна 1, то откуда с=1/(b-a).

Теперь функцию f(x) можно представить в виде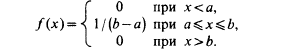

Построим функцию распределения F(x), для чего найдем выражение F(x) на интервале [a, b]:

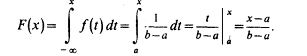
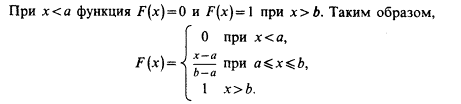
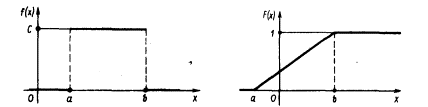
Графики функций f(x) и F(x) имеют вид:

Найдем числовые характеристики. Используя формулу для вычисления математического ожидания НСВ, имеем:

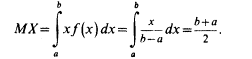
Таким образом, математическое ожидание случайной вели­чины, равномерно распределенной на отрезке [a, b] совпадает с серединой этого отрезка.

Найдем дисперсию равномерно распределенной случайной величины:

откуда сразу же следует, что среднее квадратическое отклонение:

Найдем теперь вероятность попадания значения случайной величины, имеющей равномерное распределение, на интервал (a,b), принадлежащий целиком отрезку [a, b]: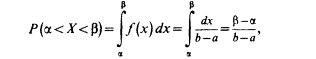 

Геометрически эта вероятность представляет  собой  площадь заштрихованного прямоугольника. Числа а и b называются параметрами распределения и однозначно определяют равномерное распределение.

33. Определение закона распределения случайной величины по статистическим данным. Методы определения параметров выбранного закона. В протокол внесено n=100 измерений случайной величины Х.

По выборке построить статистический ряд и гистограмму.

Найти статистическую функцию распределения  и построить её график.

Вычислить числовые характеристики статистического ряда  .

Выровнять полученное распределение с помощью нормального закона.

Построить график теоретической кривой распределения  в одной системе координат с гистограммой.

Построить график теоретической функции распределения  в одной системе координат с графиком функции .

Найти доверительный интервал , в котором находится точное значение математического ожидания m случайной величины Х с доверительной вероятностью  .

С помощью критерия согласия  проверить согласованность статистического и выбранного теоретического (нормального) распределения.

34. Определение закона распределения случайной величины по статистическим данным. Проверка правдоподобия гипотезы о выбранном законе. Проверка гипотез о законе распределения. Критерий согласия  . Существует несколько критериев согласия для проверки законов распределения случайной величины. Это критерии Колмогорова, Смирнова,   Пирсона и др. Мы остановимся лишь на критерии Пирсона – это наиболее часто употребляемый критерий для проверки закона распределения случайной величины. Сначала нужно разбить всю область изменения случайной величины на l интервалов (бин). Затем нужно подсчитать сколько этих величин попадает в каждый бин, то есть подсчитать эмпирические частоты тк . Чтобы вычислить теоретические частоты нужно вероятность попадания в каждый бин рк умножить на объём выборки п. Таким образом, статистика  является случайной величиной, подчиняющейся закону  с  степенями свободы.В последней формуле r – число параметров распределния, определяемы по выборке. Для нормального закона – это два параметра, для закона Пуассона – один и т.д. Рассчитав значения  и выбрав уровень значимости  , по таблице  -распределения определяют  . Если  , то гипотезу Н0 отвергают, если   то гипотезу принимают. Проверка гипотезы о равенстве дисперсий двух нормальных генеральных совокупностей  Рассмотрим две случайные величины Х и У, каждая из которых подчиняется нормальному закону с дисперсиями  . Пусть из этих генеральных совокупностей извлечены две выборки объёмамип1 и п2 . Проверим гипотезу Н0 о том, что  относительно альтернативной гипотезы Н1 , заключающейся в том, что    Однако, мы располагаем только выборочными дисперсиями  =  и  = . Задача проверки гипотезы Н0 сводится к сравнению выборочных дисперсий.  Для построения критической области с выбранной надёжностью необходимо исследовать совместный закон распределения оценок  и  . Таким законом распределения является распределение Фишера – Снедекора (или F- распределение)  Рассмотрим случайную величину  , распределённую нормально с математическим ожиданием Х и с дисперсией  . Произведём две независимые выборки объёмами п1 и п2 . Для оценки  используют выборочные дисперсии. Случайную величину, определяемую отношением  , называют величиной с распределением Фишера-Снедекора. Имеются таблицы для дифференциального закона распределения Фишера-Снедекора, которые зависят лишь от объёма выборки и уровня значимости , где k1=n1-1, k2=n2-1. Вернёмся снова к задаче проверки гипотезы о равенстве дисперсий. Сначала нужно вычислить выборочные дисперсии. Найдём отношение F= , причём в числителе поставим большую из двух оценок дисперсии. Выберем уровень значимости   и из таблиц находим число F  которое сравнивается с вычисленным F. Если окажется, что   , то проверяема гипотеза Н0отвергается, в противном случае делается вывод о том, что наблюдения не противоречат проверяемой гипотезе.

35. Показатели надежности и их классификация. Показатель надежности - количественная характеристика одного или нескольких свойств, составляющих надежность объекта.

Под номенклатурой показателей надежности понимают состав показателей, необходимый и достаточный для характеристики объекта или решения поставленной задачи. Полный состав номенклатуры показателей надежности, из которой выбираются показатели для конкретного объекта и решаемой задачи, установлен ГОСТ 27.002-89.

Показатели надежности принято классифицировать по следующим признакам:

1.               по свойствам надежности различают:

- показатели безотказности;

- показатели долговечности;

- показатели ремонтопригодности;

- показатели сохраняемости;

2.               по числу свойств надежности, характеризуемых показателем, различают:

- единичные показатели (характеризуют одно из свойств надежности);

- комплексные показатели (характеризуют одновременно несколько свойств надежности, например, безотказность и ремонтопригодность);

3.               по числу характеризуемых объектов различают:

- групповые показатели;

- индивидуальные показатели;

- смешанные показатели;

Групповые показатели – показатели, которые могут быть определены и установлены только для совокупности объектов; уровень надежности отдельного экземпляра объекта они не регламентируют.

Индивидуальные показатели – показатели, устанавливающие норму надежности для каждого экземпляра объекта из рассматриваемой совокупности (или единичного объекта).

Смешанные показатели могут выступать как групповые или индивидуальные.

4.               по источнику информации для оценки уровня показателя различают:

- расчетные показатели;

- экспериментальные показатели;

- эксплуатационные показатели;

- экстраполированные показатели;

Экстраполированный показатель надежности – показатель надежности, точечная или интервальная оценка которого определяется на основании результатов расчетов, испытаний и (или) эксплуатационных данных путем экстраполирования на другую продолжительность эксплуатации и другие условия эксплуатации.

5.               по размерности показателя различают показатели, выражаемые:

- наработкой;

- сроком службы;

- безразмерные (в том числе, вероятности событий).

36. Наработка на отказ. Поток отказов. Вероятность безотказной работы восстанавливаемого объекта. Наработка на отказ, среднее значение наработки ремонтируемого изделия между отказами (нарушениями его работоспособности). Если наработка выражена в единицах времени, то под Н. на о. понимается среднее время безотказной работы. Для периода от наработки t1 до наработки t2 Н. на о. определяется равенством

где mср — среднее число отказов (на изделие) для некоторого числа однотипных изделий до наработки ti (i = 1, 2), найденное опытным путём.

Поток отказов – последовательность отказов, возникающих одним за другим в случайные моменты времени. Если в некотором интервале t1,t2 произошло n отказов, то очевидно, что n  есть случайная величина для этого интервала и случайная функция времени для  Характеристики потоков отказов:

       а)  параметр потока отказов   - плотность вероятности отказов для рассматриваемого момента времени, т.е. предел отношения вероятности хотя бы одного отказа в интервале   к этому интервалу, 1/ч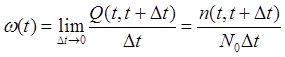

      б) интенсивность потока – математическое ожидание числа отказов в единицу времени: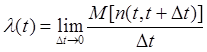

Вероятность безотказной работы определяется в предположении, что в начальный момент времени (момент начала исчисления наработки) объект находился в работоспособном состоянии. Обозначим через t время или суммарную наработку объекта (в дальнейшем для краткости называем t просто наработкой). Возникновение первого отказа - случайное событие, а наработка t от начального момента до возникновения этого события - случайная величина. Вероятность безотказной работы Р(t) объекта в интервале от 0 до t включительно определяют как  (1) Здесь Р{×} - вероятность события, заключенного в скобках. Вероятность безотказной работы ^ Р(t) является функцией наработки t. Обычно эту функцию предполагают непрерывной и дифференцируемой. Если способность объекта выполнять заданные функции характеризуется одним параметром v, то вместо (1) имеем формулу , (2) где v* и v**- предельные по условиям работоспособности значения параметров (эти значения, вообще, могут изменяться во времени). Аналогично вводят вероятность безотказной работы в более общем случае, когда состояние объекта характеризуется набором параметров с допустимой по условиям работоспособности областью значений этих параметров [8]. Вероятность безотказной работы ^ Р(t) связана с функцией распределения F(t) и плотностью распределения f(t) наработки до отказа: . (3) Наряду с понятием "вероятность безотказной работы" часто используют понятие "вероятность отказа", которое определяется следующим образом: это вероятность того, что объект откажет хотя бы один раз в течение заданной наработки, будучи работоспособным в начальный момент времени. Вероятность отказа на отрезке от 0 до t определяют по формуле . (4)

37. Наработка до отказа и характеристики ее распределения. Вероятностные и статистические методы определения характеристик.

В случае продукции не подлежащей ремонту используется термин «наработка до отказа» – наработка от начала эксплуатации до возникновения первого отказа. Характеристикой наработки является ее закон распределения.

Распределение наработки до отказа и времени восстановления системы подчинены экспоненциальному закону с функцией распределения [1] f(t) =  exp(-t).

Распределение наработки до отказа может быть описано: 1) вероятностью безотказной работы P{t); 2) плотностью распределения наработки до отказа f(t); 3) интенсивностью отказов X(t).

Вероятностью безотказной работы P(t) называют вероятность того, что случайная величина Т — наработка до отказа — будет не меньше заданной:

P(t) = P{T^t}.

Во многих задачах требуется определить вероятность безотказной работы объекта за время t — вероятность того, что в пределах заданной наработки не возникнет отказа объекта, т. е. вероятность P(tt, t2) безотказной работы в интервале наработки tu t2. Она равна отношению вероятностей безотказной работы в начале и конце интервала:

P(t1,tz) = P(t2)/P(t1).

Статистически вероятность безотказной работы определяется отношением числа объектов, безотказно проработавших до момента t, к числу объектов, работоспособных в начальный момент времени

P(t) = [N-n(ty]/N,

где N — число объектов в момент начала наблюдений или испытаний; n{t) — число объектов, отказавших за время t. Вероятность отказа объекта

e(o=i-p«-

Надежность ряда ремонтируемых объектов не всегда удобно характеризовать вероятностью безотказной работы, так как P(t) у них весьма близка к единице, особенно для небольших интервалов наработки, поэтому применяется показатель надежности — плотность распределения наработки до отказа:

f(t) = dQ(t)/dt = -dP(t)/dt;

P(t)= -J/W*-J/WA;

38. Экспоненциальное распределение наработки. Экспоненциальное распределение описывает наработку до отказа объектов, у которых в результате сдаточных испытаний (выходного контроля) отсутствует период приработки, а назначенный ресурс установлен до окончания периода нормальной эксплуатации.  Эти объекты можно отнести к «не стареющим», поскольку они работают только на участке с  (t) =  = const. Круг таких объектов широк: сложные технические системы с множеством компонентов, средства вычислительной техники и системы автоматического регулирования и т. п. Экспоненциальное распределение широко применяется для оценки надежности энергетических объектов. Считается, что случайная величина наработки объекта до отказа подчинена экспоненциальному распределению, если описывается выражением: 

f(t) =  exp( -  t),

(1)

где  – параметр распределения, который по результатам испытаний принимается равным 1 /  0 ,т где  0 – оценка средней наработки до отказа. Остальные показатели безотказности при известной f(t), определяются: 

- вероятность безотказной работы (ВБР):	P(t) =  exp ( -  t),	(2)
- вероятность отказа (ВО):	Q(t) =  1 - exp ( -  t),	(3)
- интенсивность отказов (ИО):	(t) =  exp ( - t) / exp ( -  t) =  .	(4)

Из (4) следует, что ИО является постоянной величиной, не зависящей от времени, и обратно пропорциональной оценке средней наработки  (t) =  = 1/  0 . Числовые характеристики наработки до отказа определяются: - средняя наработка (МО наработки) до отказа 

(5)

- дисперсия наработки до отказа 

(6)

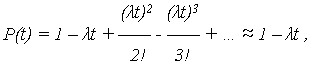Графики изменения показателей безотказности при экспоненциальном распределении приведены на рис. 1. Рис. 1 Следует отметить, что при  t < < 1, т. е. при наработке t много меньшей, чем средняя наработка T0, выражения (1) – (4) можно упростить, заменив e- t двумя первыми членами разложения e- t в степенной ряд.  Например, выражение для ВБР примет вид: при этом погрешность вычисления P(t) не превышает 0,5 ( t)2. Все рассмотренные далее законы распределения наработки до отказа используются на практике для описания надежности «стареющих» объектов, подверженных износовым отказам.