14. Проверка гипотез. Критерий χ2. Ошибки 1-го и 2-го рода. Лемма Неймана-Пирсона.

Статистической гипотезой называют любое высказывание относительно свойств генеральной совокупности (ГС), проверяемой с помощью выборочных данных.

Примерами гипотез являются:

1. гипотеза о равенстве математических ожиданий двух генеральных совокупностей (она возникает, например, когда нужно проверить одинаково ли среднее значение основных параметров изделий, производимых двумя станками, цехами)

2. гипотеза о равенстве дисперсий, когда следует сравнить точность двух измерительных приборов для измерения одной и той же величины)

3. гипотеза об однородности выборок (возникают в тех случаях, когда несколько малых выборок объединяются в одну большую и требуется до их объединения установить взяты они из одной генеральной совокупности или нет, если гипотеза подтверждается, то выборки можно объединить, иначе - нет)

4. гипотеза о законе распределения ГС (возникает в результате проведенной предварительной обработки данных (разведочного анализа), изучения гистограмм, полигона, значений выборочных коэффициентов ассиметрии)

Статистические гипотезы бывают

• параметрическими

• не параметрическими

Статистические гипотезы относительно неизвестных значений параметров распределения называют параметрическими, все другие гипотезы называются непараметрическими.

Статистическую гипотезу называют простой, если она однозначно определяет распределение генеральной совокупности, в противном случае – сложной. Если неизвестный параметр Ө принимает одно возможное значение из своих возможных значений (параметрического пространства ), то гипотезу называют простой, если принимает несколько значений, то называют сложной.

Проверяемую гипотезу H₀ называют основной, наряду с ней рассматривают одну из альтернативных гипотез H₁, противоречащих основной, например, если проверяется гипотеза H₀: Ө=Ө₀ , то альтернативными будут H₁: Ө<Ө₀ , Ө>Ө₀, Ө ≠ Ө₀. Выбор альтернативной гипотезы осуществляется конкретной постановкой задач.

Критерием проверки статистической гипотезы (К) называют правило, по которому принимают решение принять или отклонить основную гипотезу. Критерий задают с помощью критического множества (множество, попадание в которое выборки приводит к отклонению H₀): W χ_n , где χ_n – выборочное пространство (совокупность всех возможных конкретных выборок из генеральной совокупности). Принимается решение на основе конкретной выборки следующим образом:

• если конкретная выборка 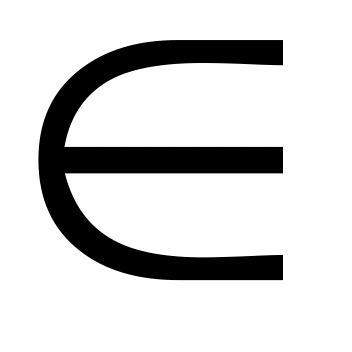W(критическому множеству), то H₀ отклоняется в пользу альтернативной;

• 2) если не принадлежит W, то принимается гипотеза H₀ и отклоняется гипотеза H₁ (гипотеза H₀ при этом считается непротиворечивой данной выборке).

При использовании любого критерия возможны ошибки 1-го и 2-го рода.

Ошибка 1-го рода – отклонить верную основную гипотезу.

Ошибка 2-го рода – это принять неверную основную гипотезу H_0.

Вероятность α совершить ошибку первого рода вычисляют по формуле: α(Ө)=P( W│H₀). Вероятность β совершить ошибку второго рода вычисляют по формуле: β(Ө)=P( │H₁), где = χ_n \ W – множество принятия основной гипотезы.

Число α такое, что вероятность ошибки первого рода не превосходит его α(Ө)≤α называется уровнем значимости критерия К. В случае простой гипотезы уровень значимости полагают равным вероятности ошибки первого рода. А величину (1-β(Ө))=m(Ө) называют мощностью критерия. Наиболее мощный критерий при заданном уровне значимости принято называть оптимальным критерием. Одновременно минимизировать α(Ө) и β(Ө) при заданном объеме выборки n нельзя, т.к.при уменьшении одной вероятности, увеличивается другая. При построении критерия для проверки параметрических гипотез, как правило, стараются максимизировать его мощность (min вероятность ошибки второго рода), при фиксированном значении вероятности α ошибки первого рода.

Построение оптимального критерия для проверки простых гипотез H₀: Ө = Ө₀, H₁: Ө = Ө₁ осуществляют на основании следующей леммы.

Лемма Неймана-Пирсона.

Л.: оптимальным критерием К* для проверки двух простых гипотез H₀: Ө=Ө₀, H₁: Ө=Ө₁, при заданном уровне значимости α является критерий К*, критическим множеством для которого является W^*:

W* = { χ_n│ },

где const C определяют исходя из условия:

С: P( ) = α

, -значение функций правдоподобия.

С помощью этой леммы можно построить оптимальный критерий проверки двух простых гипотез. Статистическая гипотеза Н₀ основывается на принципе в соответствии с которым маловероятные события считаются невозможными, т.е., если выборка попадает в критическое множество с малой вероятностью, то естественно предположить, что утверждение, которое привело к этому маловероятному событию не соответствует истине и отклонить его.

За основную гипотезу естественно принять утверждение, отклонение которого, когда оно действительно является верным, приводит к более тяжелым последствиям, нежели его принятия при справедливости альтернативного. Основную гипотезу формулируем так, чтобы она противоречила данным, иначе нет смысла ее формулировать.

Общая схема проверки параметрических гипотез выглядит так: Н₀: Ө=Ө₀

1. сначала формулируют альтернативную гипотезу Н₁ исходя из условий задачи

2. задают уровень значимости α (по умолчанию 0,05)

3. определяется выборочное распределение статистики при условии, что гипотеза Н₀ является верной

4. по заданным уровню значимости α и объему выборки n определяется критическое множество критерия К в зависимости от вида альтернативной гипотезы

5. по выборке =(x₁,x₂,…,x_n) вычисляют наблюдаемое значение статистики U_{наблюдаемое} =U( )

6. делается статистическое решение: если U_{наблюдаемое} критическому множеству W, следовательно, выборка попадает в критическое множество( W), то основная гипотеза отклоняется в пользу альтернативной. Делается вывод, что на заданном уровне значимости основная гипотеза неверна. Если выборка не принадлежит критическому множеству( W), то говорят, что выборочные данные не противоречат основной гипотезе.

Критерий («Хи-квадрат»)

Одним из наиболее широко применяемых на практике является критерий согласия, применяемый для проверки гипотез о виде распределения генеральной совокупности, для проверки гипотез об однородности выборок, о независимости признаков и т.д. Критерий согласия с основной гипотезой Н₀ принято называть критерием, в которых необходимо проверить только согласие выборочных данных с выдвинутой гипотезой. В таких критериях часто не формулируется альтернатива, подразумевая под ней все остальное. При применении этого критерия для проверки гипотезы о виде распределения в качестве меры расхождения эмпирического и теоретического (предполагаемого) законов распределения используют статистику , где n-объем выборки, r- число не пересекающихся множеств (для дискретных случайных величин) /интервалов (для непрерывных случайных величин) , на которые разбиты вся область возможных значений предполагаемой случайной величины, n_i-эмпирическая частота попадания в , p_i- вероятность того, что случайная величина попадет в множество (интервал) .

Закон распределения этой статистики при n (объем выборки)→∞ независимо от вида закона распределения случайной величины имеет теоретическое -распределение с числом степеней свободы k=r-l-1, где l- число параметров теоретического распределения, например, для нормального закона распределения N(a,σ) l=2, для экспоненциального Е( ) l=1. В целом для практики хватает n=

Общая схема проверки гипотезы Н₀: F(x, θ₁, θ₂, …)=F_T(x, θ₁, θ₂, …)

1. задается уровень значимости α;

2. по выборке находят значения оценок неизвестных параметров используя для этого, как правило, оценки максимального правдоподобия

3. область возможных значений случайной величины Х разбивают на r непересекающихся множеств , подсчитывают их эмпирические частоты при этом

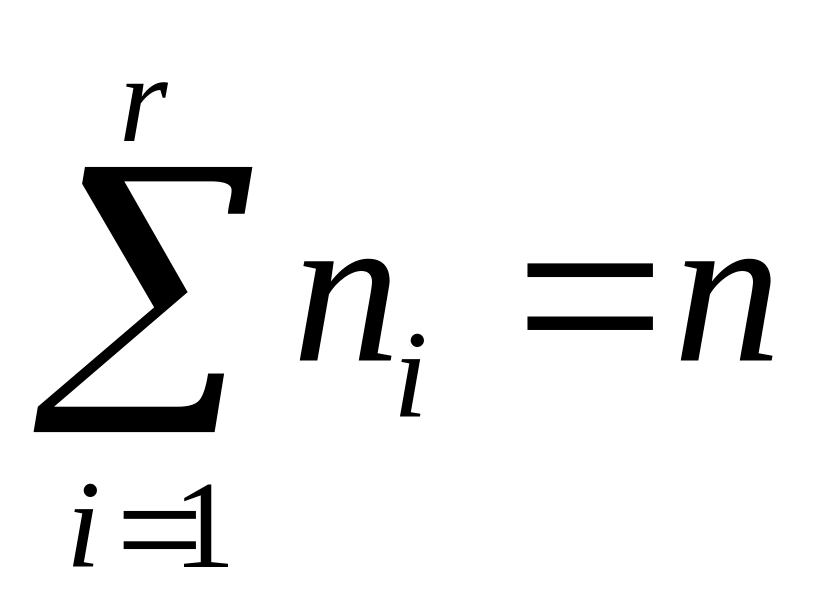
4. используя предполагаемый закон распределения Х подсчитывают вероятности 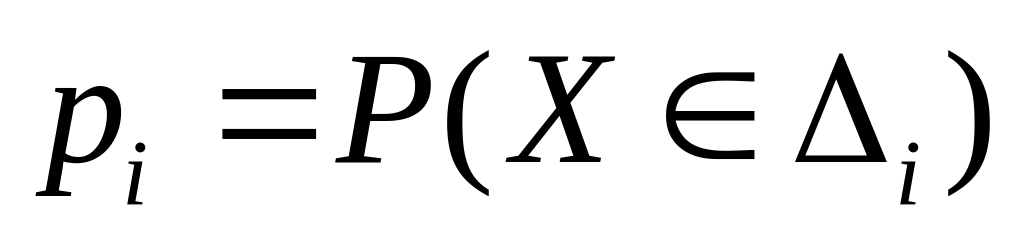. Если непрерывная случайная величина, то .

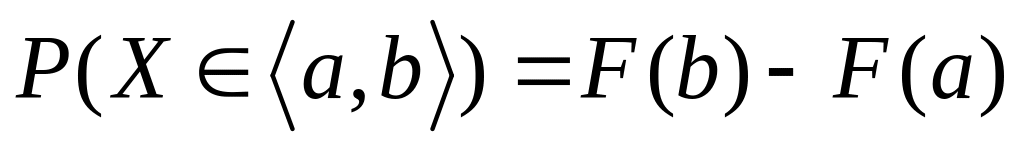Замечание: критерий использует тот факт, что случайная величина имеет распределение близкое к стандартному нормальному N(0,1) .

Чтобы это утверждение выполнялось достаточно, чтобы для всех множеств выполнялось условие для конечных объемов выборок. Если для некоторых не выполняется, то объединяем с соседними.

5. по заданным значениям α и n определяют критическое множество W критерия : )

6. по выборке 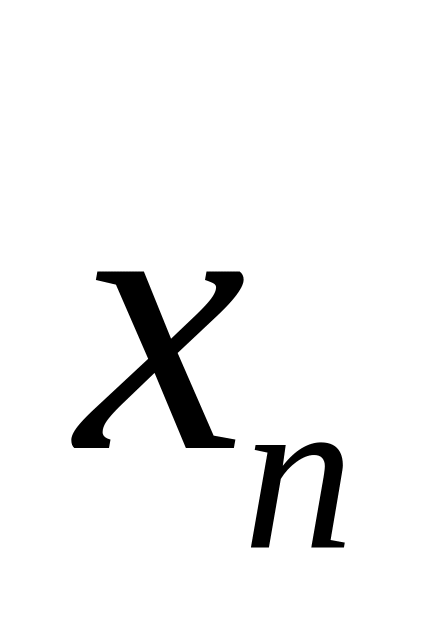вычисляют наблюдаемое значение статистики

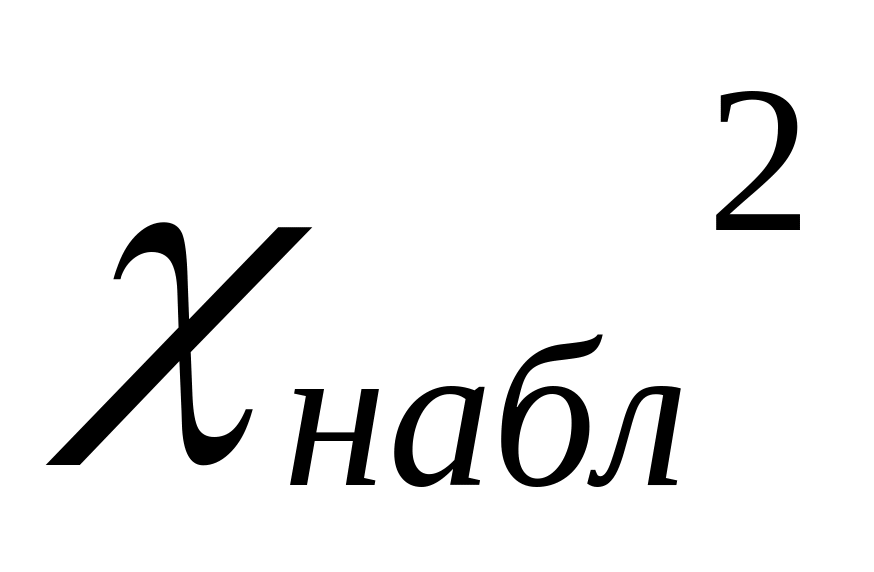
7. принимается статистическое решение: если выборка , то основная гипотеза отклоняется, как не согласующаяся с данными выборки, в противном случае принимается и делается вывод, что данные не противоречат основной гипотезе.

Статистикой в мат. статистике называют любую функцию случайной выборки y(x₁,x₂,..,x_n).