12. Закон больших чисел и центральная предельная теорема.

Под законом больших чисел понимается ряд теорем, каждой из которых устанавливается факт сходимости средних арифметических большого числа случайных величин (СВ) к некоторым неслучайным величинам (НеСВ).

Основные формы закона больших чисел – теоремы Чебышева и Бернулли.

Теорема Чебышева: пусть – последовательность независимых СВ, имеющих математические ожидания , дисперсии . Причем дисперсии ограничены одним и тем же числом , т.е. . Тогда для выполняется условие:

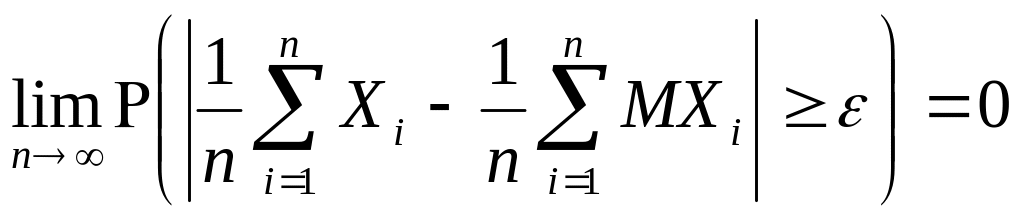или при .

Таким образом, в теореме Чебышева утверждается, что среднее арифметическое СВ при большом числе слагаемых перестает быть СВ и может быть заменено НеСВ: средним арифметическим их математических ожиданий.

Следствие из Теоремы Чебышева: в частном случае независимых одинаково распределенных СВ и . Утверждение из Теоремы Чебышева приобретает вид:

для 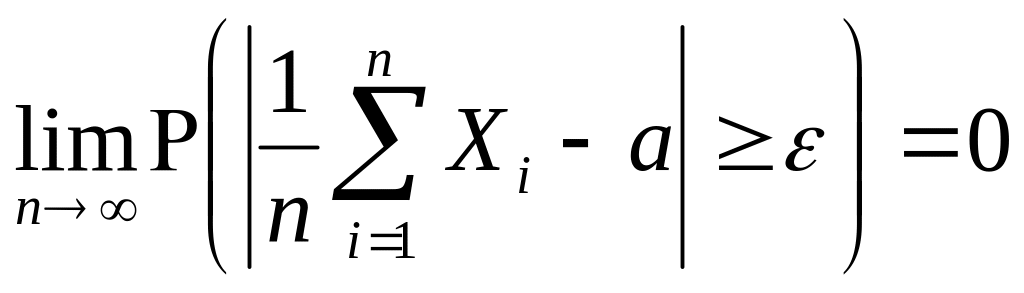или при .

В данном утверждении находит обоснование тот факт, почему в качестве истинного значения некоторой измеряемой величины используют среднее арифметическое отдельных измерений этой величины: .

Согласно данному утверждению при больших среднее арифметическое этих результатов отдельных измерений будет ближе к истинному значению, чем результат каждого отдельного измерения.

Кроме того, этот частный случай Теоремы Чебышева играет большую роль в математической статистике, являясь теоретическим обоснованием свойства состоятельности: как оценки генеральной совокупности .

В основе доказательства Теоремы Чебышева лежит неравенство Чебышева и понятие сходимости последовательности СВ по вероятности.

Неравенство Чебышева: для каждой СВ , имеющей конечную дисперсию , при имеет место неравенство . Это неравенство позволяет оценить вероятности событий, зная только и СВ , не зная закона распределения, т.е. используя минимальную информацию.

Замечание: если известен закон распределения с функцией распределения , тогда .

Последовательность СВ называется сходящейся по вероятности к некоторой величине (которая является либо СВ, либо НеСВ), если для выполняется равенство: или при .

Сходимость по вероятности означает, что последовательность приближается к так, что отклонение члена последовательности от по абсолютной величине, превосходящее любое наперед заданное число , становится все менее вероятным с увеличением .

Для доказательства Теоремы Чебышева рассматривают СВ . В силу свойств математического ожидания и дисперсии конечного числа независимых СВ и условий Теоремы следует: 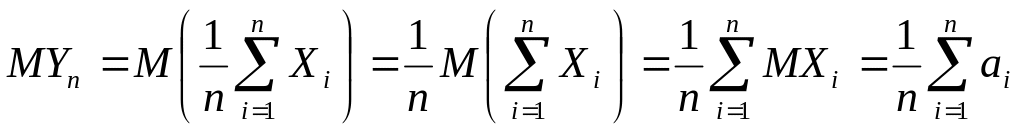( , если равны).

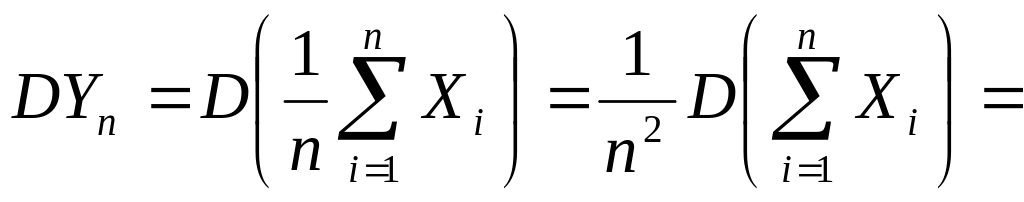{для независимых СВ}

( для одинаково распределенных СВ)

Замечание: , , .

Используя неравенство Чебышева, выполняется неравенство:

,

где и , что и требовалось доказать.

Частным случаем Теоремы Чебышева является Теоремы Бернулли (или закон больших чисел в форме Бернулли).

Теорема Бернулли: пусть в независимых испытаниях по схеме Бернулли некоторое событие в каждом из испытаний наступает с вероятностью . Тогда для выполняется:

, где - число успехов или появлений события в испытаниях, - относительная частота.

Утверждение Теоремы: при .

Доказательство Теоремы Бернулли следует из Теоремы Чебышева, если ,

0	1
1-p	p

где

Утверждение Теоремы Бернулли является теоретическим обоснованием статистического определения вероятности, тогда в качестве приближенного значения вероятности некоторого события принимают частоту его появлений, в которых данное событие появляется. Теорема Бернулли является теоретическим обоснованием состоятельности .

В Центральной Предельной Теореме (ЦПТ) исследуется вопрос возникновения нормального распределения как предельного для суммы большого числа СВ. Данная Теорема выявляет ту особую роль, которую играет нормальное распределение на практике. Нормальный закон всегда имеет место, когда СВ является результатом действия большого числа равномерно малых по их влиянию на весь результат случайных факторов, действующих независимо друг от друга.

Для случая одинаково распределенных независимых слагаемых:

ЦПТ: пусть - последовательность независимых одинаково распределенных СВ, имеющих и . Тогда функция распределения стандартизированной СВ для фиксированного при стремится к функции распределения нормальной стандартной величины : для .

Величину называют стандартизированной, если и .

В ЦПТ используется понятие сходимости последовательности функции распределения или слабой сходимости.

Сходимость называется сходимостью последовательности функции распределения к функции распределения или слабой сходимостью последовательности СВ к СВ : для слабой сходимости.