6. Пятая нормальная форма

Во всех рассмотренных до этого момента нормализациях производилась декомпозиция одного отношения в два. Иногда это сделать не удается, но возможна декомпозиция в большее число отношений, каждое из которых обладает лучшими свойствами.

Рассмотрим, например, отношение

СОТР-ОТДЕЛЫ-ПРОЕКТЫ (СОТР_НОМЕР, ОТД_НОМЕР, ПРО_НОМЕР)

Предположим, что один и тот же сотрудник может работать в нескольких отделах и работать в каждом отделе над несколькими проектами. Первичным ключем этого отношения является полная совокупность его атрибутов, отсутствуют функциональные и многозначные зависимости.

Опр. Отношение R находится в пятой нормальной форме (нормальной форме проекции-соединения PJ/NF) в том и только в том случае, когда любая зависимость соединения в R следует из существования некоторого возможного ключа в R.

Введем следующие имена составных атрибутов:

СО = {СОТР_НОМЕР, ОТД_НОМЕР}

СП = {СОТР_НОМЕР, ПРО_НОМЕР}

ОП = {ОТД_НОМЕР, ПРО_НОМЕР}

Предположим, что в отношении СОТРУДНИКИ-ОТДЕЛЫ-ПРОЕКТЫ существует зависимость соединения: (СО, СП, ОП)

На примерах легко показать, что при вставках и удалениях кортежей могут возникнуть проблемы. Их можно устранить путем декомпозиции исходного отношения в три новых отношения:

СОТРУДНИКИ-ОТДЕЛЫ (СОТР_НОМЕР, ОТД_НОМЕР)

СОТРУДНИКИ-ПРОЕКТЫ (СОТР_НОМЕР, ПРО_НОМЕР)

ОТДЕЛЫ-ПРОЕКТЫ (ОТД_НОМЕР, ПРО_НОМЕР)

Пятая нормальная форма - это последняя нормальная форма, которую можно получить путем декомпозиции. Ее условия достаточно нетривиальны, и на практике 5NF не используется. Заметим, что зависимость соединения является обобщением как многозначной зависимости, так и функциональной зависимости.

40. Реляционная алгебра, основные операторы реляционной алгебры. Связь языка sql с операторами реляционной алгебры.

Реляционная алгебра представляет собой набор операторов, использующих отношения в качестве аргументов и возвращающих отношения в качестве результата. Таким образом, реляционный оператор f выглядит как функция с отношениями в качестве аргументов: R = f(R₁, R₂, …, R_n)

В состав теоретико-множественных операций входят операции:

1. Объединения отношений (UNION). При выполнении операции объединения двух отношений производится отношение, включающее все кортежи, входящие хотя бы в одно из отношений-операндов, за исключением повторяющихся. Отношения-операнды в этом случае должны быть определены по одной схеме.

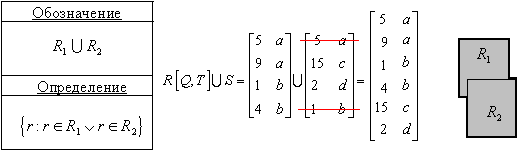
(SELECT A.x, A.b

FROM A

WHERE A.b > 1000)

UNION

(SELECT B.x, B.b

FROM B

WHERE B.b > 2000);

2. Пересечения отношений (INTERSECT). Операция пересечения двух отношений производит отношение, включающее все кортежи, входящие в оба отношения-операнда. На входе операции два отношения, определенные по одной схеме.

SELECT A.x, A.b

FROM A

WHERE A.b IN (SELECT B.b FROM B);

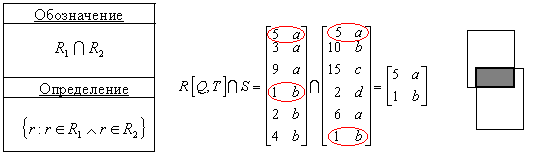
3. Взятия разности отношений (SET DIFFERENCE). Отношение, являющееся разностью двух отношений включает все кортежи, входящие в отношение - первый операнд, такие, что ни один из них не входит в отношение, являющееся вторым операндом.

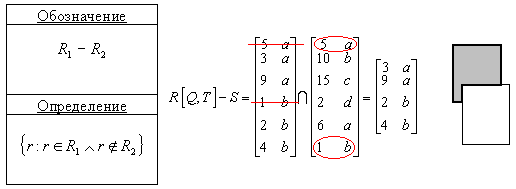
SELECT A.x, A.b

FROM A

WHERE A.b NOT IN (SELECT B.b FROM B);

4. Прямое (декартово) произведения отношений (CARTESIAN PRODUCT) При выполнении прямого произведения двух отношений производится отношение, кортежи которого являются конкатенацией (сцеплением) кортежей первого и второго операндов. Результирующее отношение состоит из всевозможных сочетаний исходных отношений. Входные отношения могут быть определены по разным схемам. Кроме того:

• степень результирующего(количество доменов) отношения равна сумме степеней исходных отношений

• мощность (количество котежей) результирующего отношения равна произведению мощностей исходных отношений.

SELECT A.x, A.z, B.c, B.d

FROM A, B;

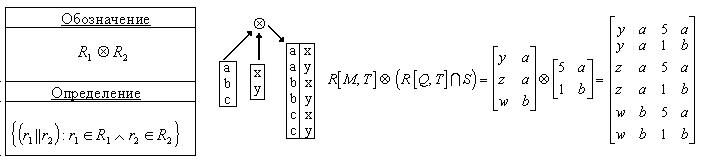
5. Ограничение отношения или выборка (горизонтальное подмножество - SELECT). На входе используется одно отношение, результат - новое отношение, построенное по той же схеме, содержащее подмножество кортежей исходного отношения, удовлетворяющих условию выборки.

SELECT A.x, A.b

FROM A;

5. Проекцию отношения - (вертикальное подмножество - PROJECT) получается выборка из каждого кортежа значений атрибутов входящих в некоторый список и удаление из полученного отношения повторяющихся кортежей(строк).

SELECT DISTINCT A.x, A.b

FROM A;

5. Соединение отношений (JOIN). Данная операция имеет сходство с декартовым произведением. Однако, здесь добавлено условие, согласно которому вместо полного произведения всех строк в результирующее отношение включаются только строки, удовлетворяющие определенному соотношению между атрибутами соединения (А1,A2) соответствующих отношений.

SELECT *

FROM A INNER JOIN B ON A.x = B.x;

5. Деление отношений. R1 и R2 – это два отношения. Результат новое отношение, структура которого получается исключением из множества атрибутов R1 множество атрибутов R2. Результирующие строки не должен содержать дубликаты.

Пр. Пусть отношение A содержит данные о поставках деталей, отношение B содержит список всех деталей, которые могут поставляться. Атрибут X - № поставщика, атрибут Y - № детали. Разделить отношение A на отношение B означает в данном примере:

"Отобрать номера поставщиков, которые поставляют все детали" эквивалентно "Отобрать те номера поставщиков из таблицы A, для которых не существует непоставляемых деталей в таблице B" эквивалентно

"Отобрать те номера поставщиков из таблицы A, для которых не существует тех номеров деталей из таблицы B, которые не поставляются этим поставщиком" эквивалентно

"Отобрать те номера поставщиков из таблицы A, для которых не существует тех номеров деталей из таблицы B, для которых не существует записей о поставках в таблице A для этого поставщика и этой детали".

SELECT DISTINCT A.x

FROM A

WHERE NOT EXISTS (SELECT *

FROM B

WHERE NOT EXISTS (SELECT *

FROM A A1

WHERE A1.x=A.x and A1.y=B.y) );

Кроме того, в состав алгебры включается операция присваивания, позволяющая сохранить в базе данных результаты вычисления алгебраических выражений, и операция переименования атрибутов, дающая возможность корректно сформировать заголовок (схему) результирующего отношения.