34. Модель с фиксированным уровнем запасов
Целесообразность создания запасов:
1) наличие запасов позволяет быстро удовлетворять потребности потребителей.
2) наличие запасов позволяет нейтрализовать колебания спроса, частично избавляя от дефицита.
Модель с фиксированным уровнем запасов основана на фиксированных моментах подачи заказа. В модели издержки управления запасами в явном виде не учитываются, и фиксированный размер заказа отсутствует.
Согласно модели через фиксированные промежутки времени производится проверка состояния запасов, и если после предыдущей проверки было реализовано какое-либо количество товара, то подается новый заказ, размер которого равен разнице максимально возможного уровня, до которого происходит пополнение, и фактического уровня в момент проверки. Максимальный уровень запасов M определяется по формуле: М = В + S (L + R), (1)
где L – время выполнения заказа,
R – интервал между проверками,
( т.е. 0, R, 2R, … – моменты проверки наличия товара на складе,
0 + L, R + L, 2R + L, … – моменты поставки заказа.)
S – среднесуточный сбыт,
В – резервный, страховой заказ, т.к. примерно в ½ случаев фактический сбыт за время доставки заказа может превысить среднее значение сбыта. Наступает временная нехватка запаса, т.е. дефицит, поэтому вводится резервный запас.
Максимальный уровень может определяться также размерами склада, тогда B и R определяются в соответствии с (1) (обычно L постоянно).
писать не надо! надо знать
Точки заказа в этой модели нет! (Например, в модели с фиксированным уровнем заказа размер заказа является постоянной величиной и повторный заказ подается при условии, что уровень наличных запасов снижается до определенного критического уровня, который в теории управления запасами называется точкой заказа).
В этой системе размер заказа определяется следующими правилами. В моменты проверки можем сделать заказ в размере:
q0 – последний на очереди невыполненный заказ
I – фактический уровень запасов, наличные запасы, текущий размер запаса
Пусть L R
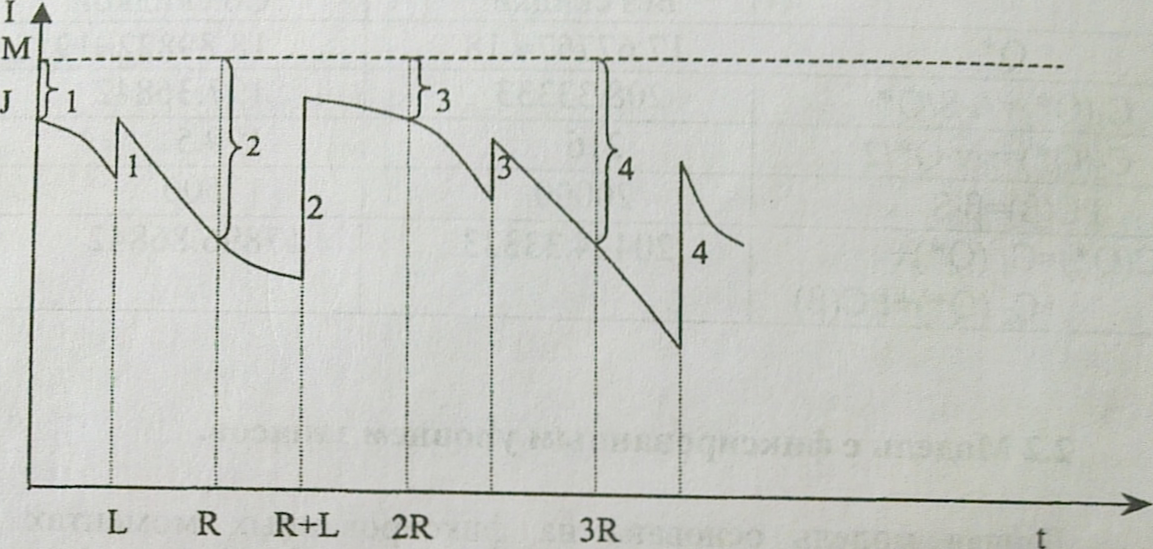
1 – формирование /1- выполнение заказа
(максимум может достичься, если нет сбыта в течениие одной проверки)
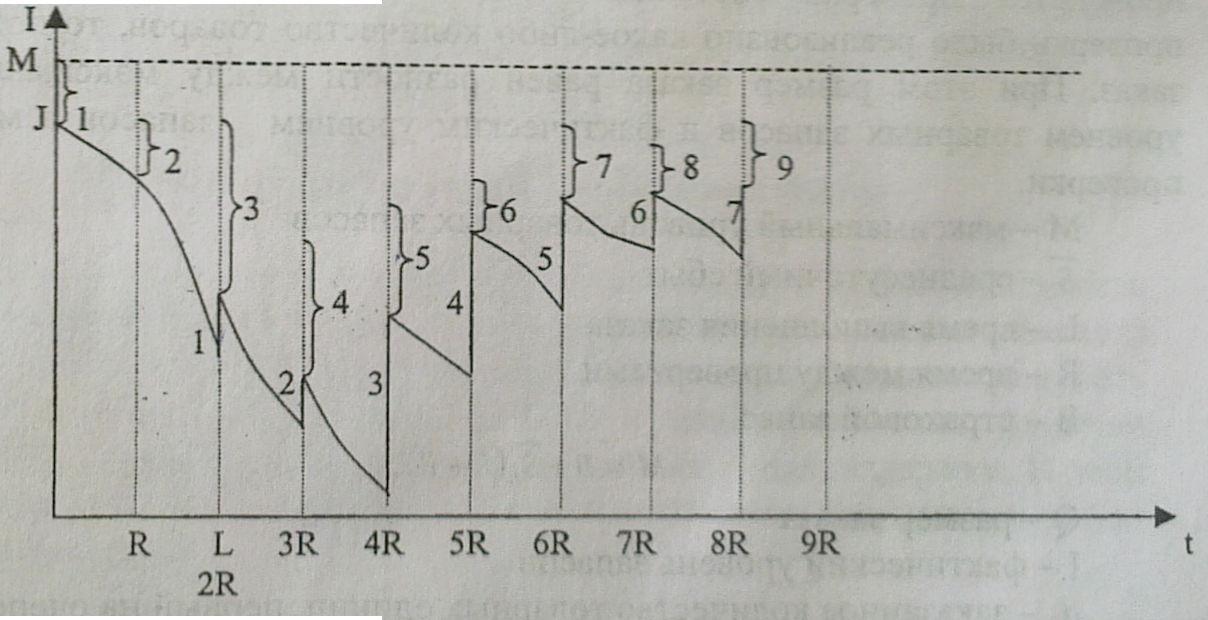
Пусть L > R
(максимум может достичься, если нет сбыта в течениие двух проверок)
В этой модели сначала выполняется заказ, а потом формируется следующий. Чем больше спрос, тем больше заказ.
Максимальный запас М достигается в том случае, если в интервале между проверками отсутствует сбыт. Размер заказа зависит от величины сбыта после последней проверки. Средний уровень запасов I = B + S*R/2. Размер резервного запаса можно определить достаточно точно рассматривая распределение сбыта за промежуток времени L + R.
При использовании метода с фиксированным уровнем запасов, даже при самом плохом стечении обстоятельств, склад никогда не будет переполнен, т.к. идет вычисление размера склада
Рекомендации по выбору:
Эта модель более предпочтительна в том случае, когда поставка товаров происходит в жестко установленные сроки, также она часто выбирается когда требуется быстро реагировать на изменение сбыта.
Но эта модель не позволяет учитывать издержки в явном виде. Если издержки незначительны и их невозможно вычислить, то ее также можно использовать.
Также эта модель предпочтительнее, когда на общий размер заказов, подаваемых одним клиентом, налагаются ограничения грузоподъемности транспортных средств.
Эту модель целесообразней использовать при периодических проверках запасов.