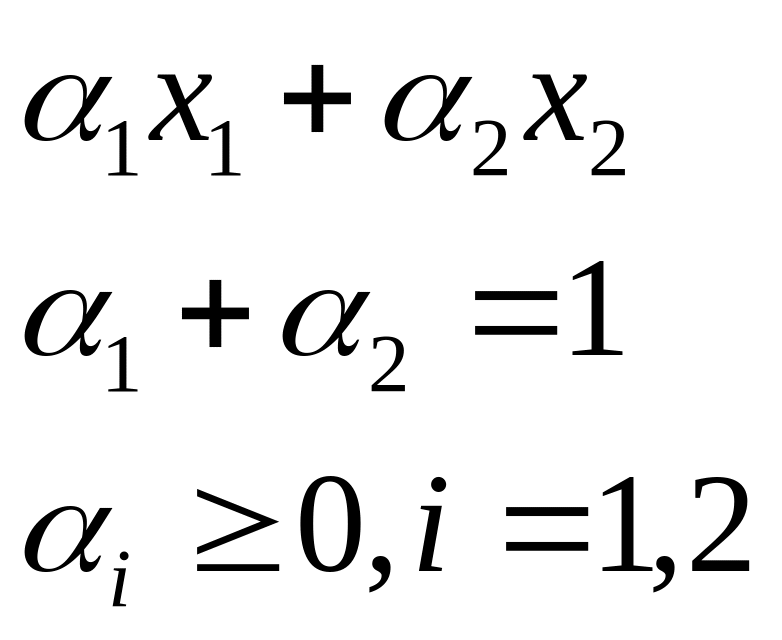- •3. Системы линейных алгебраических уравнений. Условие сущ-ния решения, решение систем по формулам Крамера и методом исключений, фундаментальная система реш-й.
- •5. Пределы и непрерывность. Числовая последовательность и ее предел. Определение функции, ее непрерывность на языке "эпсилон-дельта" и языке пределов, равномерная непрерывность.
- •6, Производная функция одной переменной. Определение, геометрический смысл, простейшее правило вычисления производной. Производная сложной функции. Формула Тейлора.
- •8. Определенный интеграл и его геометрический смысл (задача о площади криволинейной трапеции). Приближенное вычисление определенных интегралов, формулы трапеций и Симпсона.
- •12. Закон больших чисел и центральная предельная теорема.
- •13. Регрессионный анализ: линейная и нелинейная регрессия, статистические свойства оценок коэффициентов регрессии.
- •14. Проверка гипотез. Критерий χ2. Ошибки 1-го и 2-го рода. Лемма Неймана-Пирсона.
- •15. Метод максимального правдоподобия. Точечное и доверительное оценивание параметров гауссовского распределения.
- •Вопрос 16: Тренд, сезонная и циклическая компоненты временного ряда.
- •17.Модели тренда (свойства логистической и линейной кривой).
- •18. Методы выделения сезонной компоненты временного ряда (метод скользящих средних).
- •19. Приведение задач линейного программирования к каноническому виду. Методы искусственного базиса.
- •I метод искусственного базиса
- •II метод искусственного базиса
- •20. Симплексный метод (см), основные принципы, алгоритм.
- •21. Двойственный симплекс-метод, основные принципы, алгоритм. Случаи, когда удобно применять двойственный симплексный метод. (дсм)
- •22. Задача максимизации прибыли при заданных ценах на продукцию и ресурсы. Анализ оптимальных решений с помощью множителей Лагранжа.
- •23. Транспортная задача замкнутого типа: постановка, существование решения, метод потенциалов.
- •24. Транспортная задача незамкнутого типа. Постановка, способ сведения к задаче замкнутого типа(с обоснованием). Алгоритм решения.
- •25. Теорема о необходимых и достаточных условиях оптимальности смешанных стратегий. Метод сведения решения игр к решению задачи линейного программирования.
- •26. Функция выигрыша в матричных играх без седловой точки. Смешанные и оптимальные смешанные стратегии. Метод сведения решения матричных игр к задаче линейного программирования.
- •27. Методы наискорейшего и координатного спуска для минимизации выпуклой функции без ограничений. Их алгоритмы и геометрическая интерпретация
- •28. Типичные производственные функции с несколькими ресурсами: линейная пф, степенная пф, пф с постоянными пропорциями. Коэффициенты эффективности использования ресурсов для этих типов функций
- •1. Линейная производственная функция:
- •2. Степенная производственная функция:
- •3. Производственная функция с постоянными пропорциями:
- •33. Модель с фиксированным размером заказа
- •34. Модель с фиксированным уровнем запасов
- •35. Двухуровневая система управления товарными запасами, (s,s)-система.
- •36. Математическая модель и схема статического моб в денежном выражении. Методологические вопросы построения моб.
- •Методологические вопросы построения моб Классификация отраслей
- •Метод учета продукции
- •Способ оценивания продукции
- •Общие предпосылки модели моб
- •Дополнение ограничений моб по производственным ресурсам
- •37. Свойства коэффициентов прямых материальных затрат в моб. Определение косвенных и полных материальных затрат.
- •38. Основные понятия теории баз данных: объект, свойство, связь. Диаграмма «сущность-связей». Логическая, физическая, концептуальная схемы базы данных
- •39. Реляционная модель данных. Основные понятия: отношение, кортеж, домен. Получение нормальных форм отношений из диаграммы «сущность-связь». Реляционная алгебра и ее основные понятия.
- •Первая нормальная форма
- •Вторая нормальная форма
- •Третья нормальная форма
- •Нормальная форма Бойса-Кодда
- •Четвертая нормальная форма
- •Пятая нормальная форма
- •40. Реляционная алгебра, основные операторы реляционной алгебры. Связь языка sql с операторами реляционной алгебры.
- •41. Реляционная модель данных. Теория нормализации. Нормальные формы: первая, вторая, третья, Бойса-Кодда.
- •42. Физическая организация баз данных. Файлы: последовательные, с прямым доступом, с хеш-адресацией, индексно-последовательные, в-деревья.
- •43. Назначение и основные компоненты операционных систем. Управление памятью. Управление внешними устройствами. Защита данных. Интерфейс прикладного программирования. Пользовательский интерфейс.
- •Пользовательский интерфейс
- •47. Функция организационного управления: сбор и первичная обработка данных, моделирование ситуации выбора, прогнозирование неуправляемых параметров
- •Сбор и первичная обработка данных
- •Моделирование ситуации выбора
- •Идентификация модели ситуации выбора (прогнозирование неуправляемых параметров)
- •48. Функция организационного управления: планирование, принятие решения организация исполнения решения, контроль, координация.
- •Планирование (вычисление управляемых параметров)
- •Принятие решений
- •Организация исполнения решений
- •Контроль
- •Координация
- •Вопрос 11. 20
- •Вопрос 16: Тренд, сезонная и циклическая компоненты временного ряда. 31
23. Транспортная задача замкнутого типа: постановка, существование решения, метод потенциалов.
Формулировка транспортной задачи (ТЗ): имеется m поставщиков (пунктов отправления) А1, …, Am, у которых имеется однородный груз в кол-вах а1, …, аm. В этом товаре нуждается n потребителей В1, …, Вn, каждый в кол-ве b1, …, bn. Т.ж. известны так называемые коэф-ты затрат сij = стоимости перевозки груза от постав Аi к потреб Вj. Данные удобно записывать в распределительной матрице:
потр пост |
В1 |
… |
Вn |
|
b1 |
… |
bn |
||
А1 |
а1 |
с11 х11 |
… |
с1n х1n |
… |
… |
… |
… |
… |
Am |
аm |
сm1 хm1 |
… |
сmn хmn |
Постановка ТЗ: необходимо найти такой план перевозок, чтобы:
мощности всех поставщиков были реализованы
спрос всех потребителей был удовлетворителен
суммарные затраты на перевозки были мин-ми
С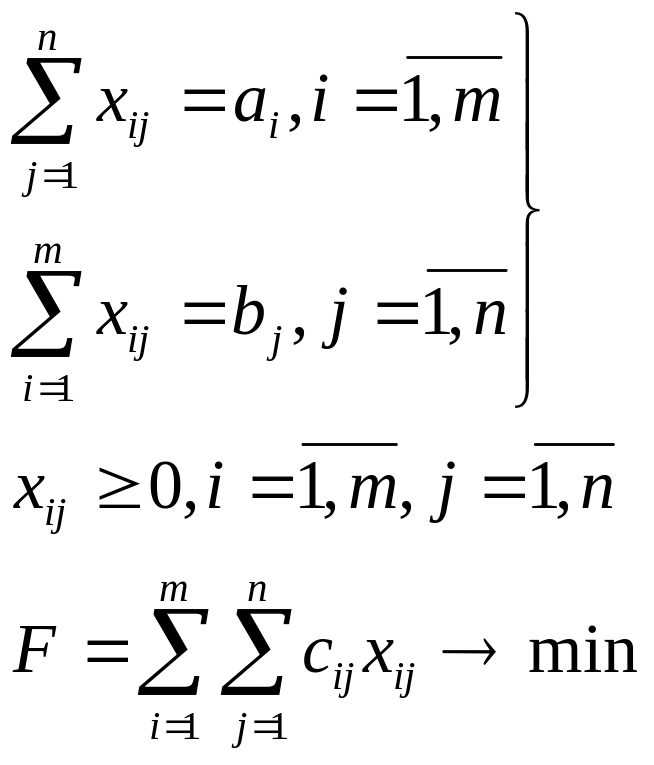 оставим
эк-ко-мат-ую модель ТЗ, т.е. запишем на
мат-ом языке зад-ые усл-ия. Обоз-им ч/з
хij – кол-во ед-ц
груза, к-ый необх. доставить от поставщика
аi к потребителю
bj.
Матрица, сост-щая из хij
наз-ся матрицей перевозок, а из сij
– матрицей тарифов.
оставим
эк-ко-мат-ую модель ТЗ, т.е. запишем на
мат-ом языке зад-ые усл-ия. Обоз-им ч/з
хij – кол-во ед-ц
груза, к-ый необх. доставить от поставщика
аi к потребителю
bj.
Матрица, сост-щая из хij
наз-ся матрицей перевозок, а из сij
– матрицей тарифов.
Мощности всех поставщиков д.б. реализованы
(1)
Спрос всех потреб-лей д.б. удовл-н
(2) По смыслу поставка не м.б. отр-ной
(3) Суммарные затраты на перевозку ТЗ закл-ся в нах-ии хij, удовл-щие (1), (2), при к-ых (3) принимает наим-ее значение.
План перевозок х наз-ся допустимым, если он удовл-ет (1) и (2). Распред-ие поставок наз-ся оптимальным, если оно доставляет мин-м (3).
Т. о
сущ-ии допустимого плана: для того,
чтобы ТЗ имела допустимый план необх.
и дост., чтобы ТЗ была закрытой
![]() ,
т.е. суммарная мощность поставщиков
совпадала с суммарным спросом потребителей.
,
т.е. суммарная мощность поставщиков
совпадала с суммарным спросом потребителей.
Т. о
ранге матрицы: Ранг матрицы коэф-тов
системы (1) = m+n-1.
(Если спросят написать):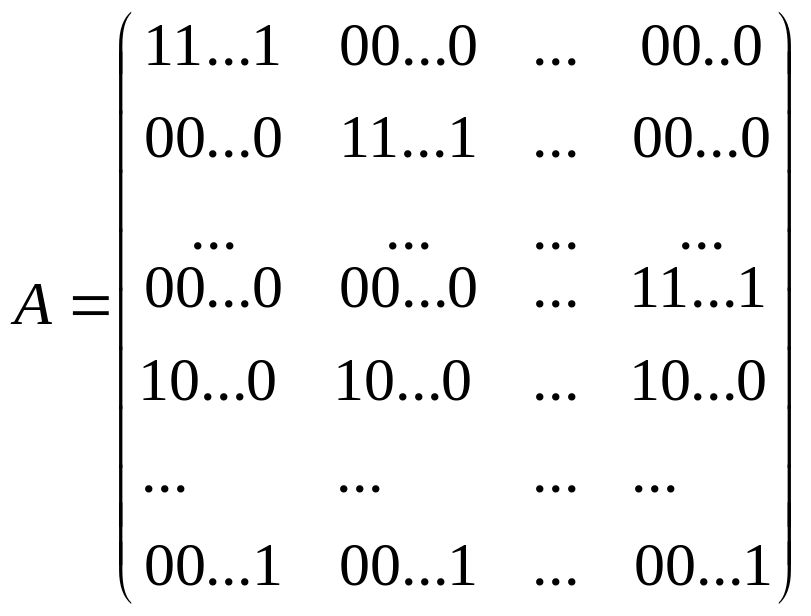
Решение закрытой ТЗ:
нах-ся любое допустимое распред-ие поставок
это распред-ие перестр-ся, чтобы мин-ть затраты
н-р, эту з-чу м. решить с пом. мет. наим. затрат. Согласно этому мет. В нач. дается макс-но возм-ная поставка в клетку с наим-им коэф-том затрат. Эту клетку сч-т заполненной, для удобства перечерк-т сплошной линией. Выпавшие из дальнейшего рассм-ия клетки наз-т свободными и перечер-т пунктирными линиями. Затем процедура повт-ся в непрочер-ых никакими линиями клетках. После этого дел-ся проверка: кол-во заполн-х клеток д. = m+n-1. Если их меньше, то вводим фиктивные нулевые поставки до треб-го кол-ва. Вводят их т.о., чтобы не образ-ся квадрат или прямоугольник из заполн-ых клеток (иначе невозм-но будет найти потенциал).
м-д потенциалов.
Он основан на Т. о потенциалах: Если
х* есть оптимальный план поставок,
то ему соотв-т система чисел (ui*,vj*),
i=1,m,j=1,n,
наз-ых потенциалами строк и столбцов
(поставщиков и потребителей), удовл-щих
усл-ию:
![]()
Исп-уя эту теорему, мы м. найти эти числа.
Для этого u1 полагают
=0 (м. = любому числу), остальные потенциалы
нах-ся по заполненным клеткам по след-щей
ф-ле:
![]() .
.
После того, как были найдены все потенциалы
нах-т Эл-ты матрицы оценок по ф-ле:
![]() .
.
Для заполн-ых клеток эл-ты этой матрицы =0. Если для незапол-ых клеток все >=0, то по теореме мы нах-м оптимальное распред-ие. Если же среди оценок есть отриц-ые, то распред-ие точно не оптимальное и перераспред-т поставки, а именно строят цикл пересчета. Для этого берут любую свободную клетку с отриц-ой оценкой наз-т вершиной цикла, далее двиг-ся по некот-ым заполн-ым клеткам так, чтобы вернуться назад, двиг-ся под прямыми углами. В одной строчке или столбце м.б. лишь одно звено.
Вершине цикла усл-но ставим «+», затем знаки черед-ся(в цикле всегда четное кол-во клеток). Затем из тех клеток, где «-» выбираем наим-ую поставку и ее вычитаем из всех клеток, где «-», и прибавляем, где «+». Измененные значения цикла вставляем в исходную таблицу и снова нах-м потенциалы и матрицы оценок.
Альтернативное решение.
Если оценка получается в оптимальном
решении =0 в свободной клетке. Выбираем
вершину, создаем цикл, получаем новое
решение и составляем выпуклую линейную
комбинацию вида: