18. Методы выделения сезонной компоненты временного ряда (метод скользящих средних).

Многие временные ряды, особенно экономические, содержат сезонные компоненты, которые могут как представлять интерес сами по себе, так и выступать в роли мешающего фактора (при изучении, например, основной тенденции развития). В обоих случаях необходимо уметь выделять сезонную компоненту и в случае необходимости устранять её из ряда.

Один из наиболее известных методов выделения сезонной компоненты- метод скользящих средних. Метод основан на переходе от начальных значений уровней ряда:

, , ,…,

к усреднённым значениям:

, , ,…, .

Для выделения и оценки сезонной компоненты число периодов сезонности в исследуемом временном ряде должно быть (например, при рассмотрении месячных или квартальных данных необходимы наблюдения как минимум за 5-6 лет).

Усреднение начальных значений уровней ряда проводится на интервале времени, называемом интервалом сглаживания, длина которого выбирается заранее, при этом сам выбранный интервал как бы скользит вдоль ряда. Для сезонных временных рядов длина интервала сглаживания, как правило, выражается чётным числом (4,12,…) и выбирается равной периоду сезонности (или кратной ему). Например, для ежеквартальных данных – 4, для ежемесячных -12 и т.д.

Если длина интервала сглаживания – чётное число, т.е. , то усреднённые значения , ( ) (скользящие средние) вычисляют по формуле:

.

Например, если , то - по формуле:

,

в частности, при : ,

при : и т.д.

При этом при усреднении первые и последние членов исходного ряда будут отброшены.

Таким образом, в случае усреднения, когда длина интервала сглаживания задаётся чётным числом , для усреднения используют значений уровней исходного ряда, но крайние значения выбирают с весом . Связан такой выбор с тем, что если рассчитать по формуле , то полученное усреднённое значение следовало бы сопоставить уровню исходного ряда, которого в исходном ряде нет.

Для несезонных рядов длину интервала сглаживания задают нечётным числом (3,5,7,…) и усреднённое значение вычисляют по формуле:

.

Выделение и оценка сезонной компоненты осуществляется следующим образом.

Предполагается, что модель временного ряда имеет вид: .

Сначала, методом скользящей средней находят оценку трендовой компоненты , которая и выражается усреднёнными значениями и строят ряд скользящих средних. При этом первые и последние членов исходного ряда в ряде скользящих средних окажутся отброшенными. В результате будут получены два ряда (при ):

, , , ,…, , , ,

, ,…, , .

Полученные ряды, учитывая наличие сезонов (для ежеквартальных данных сезоном является квартал, для ежемесячных – месяц и т.д.), представляют затем в преобразованном виде и записывают в виде следующей таблицы (при , ):

	1		2		3		4		5
1		-
2		-
3										-
4										-

Здесь - номер сезона ( ), -номер периода сезонности ( ), - число периодов сезонности (например, для ежеквартальных и ежемесячных данных период сезонности - год), и - значения уровней исходного и усреднённого сезонных рядов в -ом сезоне -го периода сезонности.

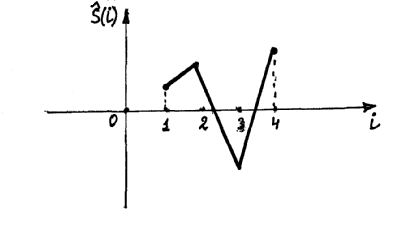
В качестве простейшей оценки сезонной компоненты используют усреднённые по периодам сезонности значения разностей : , . Совокупность значений называют при этом сезонной волной. Графическое изображение сезонной волны даёт наглядное представление о сезонных отклонениях значений уровней исходного ряда от усредненных значений (являющихся оценкой трендовой составляющей), периодически повторяющихся в каждом периоде сезонности.

Для удаления сезонной компоненты из значений уровней исходного ряда вычитают для всех . Получают ряд:

, , , ,…, , , , ,

который записывают, как правило, опять в виде: , где - значение уровня исходного ряда, не содержащего сезонной компоненты .