
25. Общие сведения о геодезической сети. Геодезическая сеть представляет собой совокупность закрепленных на местности пунктов, для которых в единой системе определены координаты и высоты. Основной принцип построения геодезической сети – от общего к частному. Геодезические сети могут быть плановыми, высотными или одновременно теми и другими. Плановая сеть устанавливает взаимное положение точек на плоскости или на поверхности земного сфероида. Создается она методами триангуляции, полигонометрии, трилатерациииGPS.При методе триангуляции в треугольниках измеряют все углы и минимум две стороны на разных концах сети (вторая сторона для контроля). Остальные стороны вычисляют, используя теорему синусов. Для вычисления координат всех точек надо знать координаты хотя бы одной точки и дирекционный угол одной линии. Метод полигонометрии заключается в построении сети ходов, в которых измеряются все углы и стороны. Полигонометрические ходы отличаются от теодолитных более высокой точностью измерений. Метод трилатерации отличается от триангуляции тем, что в треугольниках измеряются не углы, а стороны. Для измерения сторон обычно используют электронные дальномеры. Углы вычисляются по измеренным сторонам, например, по теореме косинусов.GPS– система глобального позиционирования. Имеет параллельное название – NAVSTAR.Параллельнос американской GPS в России разви-вается система ГЛОНАСС (ГЛОбальнаяНавига-ционнаяСпутниковая Система).Высотная геодезическая сеть устанавливает положение точек относительно уровня моря. Она создана для распространения по всей территории страны единой системы высот. За начало высот принимают средний уровень Балтийского моря. Она создается методами геометрического,тригонометрического и барометрического нивелирования.Геодезические сети подразделяются на 3 вида:1. Государственная геодезическая сеть (ГГС).2. Геодезические сети сгущения (ГСС).3. Съемочные сети.
30.Последовательность видов работ при построении триангуляции. При создании геодезических сетей методом триангуляции выполняют следующие виды работ:1. Составление технического проекта сети по карте. 2. Рекогносцировка на местности вершин треугольников и выходных сторон. 3. Закладка центров и постройка триангуляционных знаков в вершинах треугольников. 4.Определение значений длин и дирекционных углов выходных сторон. 5. Измерение углов треугольников.6.Обработка результатов измерений (предварительная обработка, уравнивание, вычисление координат и составление каталогов пунктов).
26.
Государственная геодезическая сеть.
ГГС
называют сеть закрепленных точек земной
поверхности, обеспечивающей распространение
единой системы координат на территорию
государства и являющейся исходной для
создания других геодезических сетей.
ГГС является главной геодезической
основой топографических съемок всех
масштабов. Геодезическая основа
Республики Беларусь реализована в виде
ГГС, ранее созданной на территории
бывшего СССР. Государственная
(опорная) геодезическая сеть СССР
подразделялась на:а) сети триангуляции,
полигонометрии и трилатерации 1, 2, 3 и
4 классов;б) нивелирные сети I,
II, III, IV классов.Триангуляция 1 класса
строилась в виде системы замкнутых
полигонов периметром 800–1000 км.Полигоны
образовывали триангуляционными рядами,
которые стремились разместить в
направлении меридианов и параллелей.
Длина звена около 200 км. В местах
пересечения звеньев измеряли базисные
стороны. На обоих концах базисных сторон
определяли астрономические широты,
долготы и азимуты. Если условия местности
не позволяют разбить сеть триангуляции,то
прокладывают хода полигонометрии 1-го
класса. В дальнейшем сеть сгущается
развитием сплошной триангуляции 2-го
класса, либо ходами полигонометрии
2-го класса. В дальнейшем сеть может???
триангуляцией
3-го и 4-го класса или полигонометрией
в виде сетей или отдельных ходов.
Достоинством полигонометрии является:
простота геометрического построения
сетей ,большая гибкость, экономия затрат
труда. Недостатки :слабый контроль
угловых и линейных измерений, менее
равномерная плотность сети по сравнению
с триангуляцией.В целях долговременной
сохранности сетей их пункты закрепляют
на местности особо надёжными сооружениями
– центрами
.В зависимости
от климатических и природных условий
применяют различные виды центров.
 Над
центрами пунктов сооружают наружные
знаки, которые служат визирными целями
при измерении углов и линий (туры,
пирамиды, простые сигналы, сложные
сигналы).Для каждого пункта сети
определяется его высота методом
геометрического или тригонометрического
нивелирования. Государственная
нивелирная сеть является главной
высотной основой для решения научных
и инженерно-технических задач. Создается
методом геометрического нивелирования.СетиI
и II классов
обеспечивают
единуюсистему высот на территории всей
страны, а также используются для научных
целей. Сети III
и IV классов
служат для обеспечения топографических
съёмок и решения инженерных задач.Предельные
невязки в превышениях нивелирных ходов
определяются по формулам
Над
центрами пунктов сооружают наружные
знаки, которые служат визирными целями
при измерении углов и линий (туры,
пирамиды, простые сигналы, сложные
сигналы).Для каждого пункта сети
определяется его высота методом
геометрического или тригонометрического
нивелирования. Государственная
нивелирная сеть является главной
высотной основой для решения научных
и инженерно-технических задач. Создается
методом геометрического нивелирования.СетиI
и II классов
обеспечивают
единуюсистему высот на территории всей
страны, а также используются для научных
целей. Сети III
и IV классов
служат для обеспечения топографических
съёмок и решения инженерных задач.Предельные
невязки в превышениях нивелирных ходов
определяются по формулам
I
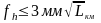 кл
кл
I Iкл
Iкл
IIIкл
I Vкл
Vкл
L-длина хода в км
Рассмотренная ГГС строилась по единойпрограмме на территорию всего Советского Союза в течение многих десятилетий. Она включала около 164 тыс. пунктов 1 и 2 классов. Натерритории Беларуси таких пунктов было около 2,5 тыс. Плановые сети в течение многих лет не обновлялись. По своему состоянию и точности они уже не отвечают современным требованиям. Поэтому в России и РБ разработаны программы модернизации ГГС на основеспутниковых методовопределения координат.
27. Государственная геодезическая сеть РБ.ГГС РБ предназначена для:1)распространения единых установленных систем координат на территории Республики Беларусь;
2)геодезического обеспечения картографирования территории Республики Беларусь;
3) геодезического обеспечения изучения земельных ресурсов и землепользования, создания кадастров, строительства, разведки и освоения природных ресурсов Республики Беларусь;
4)Решение геодезических задач.
ГГС является носителем геодезической системы координат и высот Республики Беларусь. Началом единого отсчета плановых координат служит центр круглого зала Пулковской обсерватории в Санкт-Петербурге. При производстве геодезических и картографических работ государственного назначения на территории Республики Беларусь применяется единая система геодезических координат и Балтийская система высот.ГГС состоит из взаимосвязанных геодезических сетей различных классов точности, создаваемых по принципу от общего к частному.
ГГС включает:
1)фундаментальную астрономо-геодезическую сеть (ФАГС);
2)высокоточную геодезическую сеть (ВГС);
3)спутниковую геодезическую сеть 1-го класса (СГС-1);
4)геодезические сети сгущения (ГСС).
ВГС представляет собой пространственное геодезическое построение, опирающееся на пункт ФАГС и геодезические пункты других государств. Расстояние между пунктами ВГС должно составлять 150–300 км.
Спутниковая геодезическая сеть 1 класса (СГС-1) представляет собой пространственное геодезическое построение, опирающееся на пункты ФАГС и ВГС.
Расстояние между пунктами CГС-1 должно составлять 15–25 км, а на территориях городов, больших промышленных объектов – 8–12 км.
28. Сети сгущения.
Геодезические сети сгущения создаются на основе государственной сети для обоснования топографических съёмок масштабов 1:5000– 1:500. При этом в основном применяются те же методы, как и в государственных сетях.
Они подразделяются на аналитические сети триангуляции 1 и 2 разрядов, полигонометрические сети 1 и 2 разрядов и сети технического нивелирования
Триангуляция 1 и 2 разряда обычно строится в виде типовых фигур
а)![]() б)
б)![]() Д)
Д)![]()
в)![]() г)
г)![]()
а) Вставка в угол
б)геодезический четырехугольник
в)центральная система
г)цепь треугольников между исходными сторонами
д)Цепь треугольников между исходными пунктами
Минимальный угол в сплошной сети 1 и 2 разрядов – 20°, в цепочке треугольников – 30°. Число треугольников между исходными пунктами не более 10. Минимальная длина выходной стороны 1 км.
Плановые сети сгущения можно создавать также методом трилатерации, полярно-лучевым методом и др.
Высотные сети сгущения создаются техническим нивелированием. Длины визирного луча допускается до 150 м. Предельная невязка в сумме превышений определяется по формуле

 Или
Или
Где L-длина хода в км
n-число станций в ходе
29.Cъемочные сети являются непосредственной основой съёмок всех масштабов и других геодезических работ. Они могут строиться на основе государственных сетей, сетей сгущения или в условной системе координат.
Точность съёмочных сетей устанавливаются соответствующими инструкциями.
При создании плановых съёмочных сетей применяется метод триангуляции, трилатерации, теодолитные хода, полярно-лучевой метод, различные засечки и др.
Высотыточек съёмочного обоснования определяются геометрическим или тригонометрическим нивелированием.
Д опустимые
невязки в превышениях определяются по
формулам:
опустимые
невязки в превышениях определяются по
формулам:
 -
при техническом нивелировании;
-
при техническом нивелировании;
 -
При нивелировании горизонтальным лучом
теодолитом или кипрегелем
-
При нивелировании горизонтальным лучом
теодолитом или кипрегелем
-при тригонометрическом нивелировании
3 1.
Приведение
измеренных направлений к центрам
пунктов.Геодезический
знак стремятся строить так, чтобы ось
визирного цилиндра находилась на одной
отвесной линии с центром знака.
Практически это условие не всегда
выполняется. Вследствие этого при
измерении углов прибор часто устанавливают
не над центром пункта и наблюдают на
визирные цели смежных пунктов, оси
которых не совпадают с отвесными линиями
центров пунктов. В таких случаях в
измеренные направления вводятся
поправки за центрировку
и редукцию.
Пусть в момент измерения направлений
центр пункта находился в точкеС,
а прибор в точке Р.
1.
Приведение
измеренных направлений к центрам
пунктов.Геодезический
знак стремятся строить так, чтобы ось
визирного цилиндра находилась на одной
отвесной линии с центром знака.
Практически это условие не всегда
выполняется. Вследствие этого при
измерении углов прибор часто устанавливают
не над центром пункта и наблюдают на
визирные цели смежных пунктов, оси
которых не совпадают с отвесными линиями
центров пунктов. В таких случаях в
измеренные направления вводятся
поправки за центрировку
и редукцию.
Пусть в момент измерения направлений
центр пункта находился в точкеС,
а прибор в точке Р. Расстояние
CP=еназывается
линейным
элементом центрировки.
Угол Θ,
отсчитываемый при точке Р
от направленияС
до начального направления N
по ходу часовой стрелки, называется
угловым
элементом центрировки. Фактически
измерено направление РN,
а надо было измерить СN.
Проведем СN'
// PN,
тогда угол сN
выразит поправку в направление. Из Δ
CNPимеем
Расстояние
CP=еназывается
линейным
элементом центрировки.
Угол Θ,
отсчитываемый при точке Р
от направленияС
до начального направления N
по ходу часовой стрелки, называется
угловым
элементом центрировки. Фактически
измерено направление РN,
а надо было измерить СN.
Проведем СN'
// PN,
тогда угол сN
выразит поправку в направление. Из Δ
CNPимеем
О тсюда
тсюда
П о
малости угла сN
можно записать
о
малости угла сN
можно записать
А налогично
можно найти поправку в любое направление.
Например, поправка в направление на
пунктК
составит
налогично
можно найти поправку в любое направление.
Например, поправка в направление на
пунктК
составит
г де
МK–
величина измеренного направления на
пункт К.В
общем виде без индексов формулу для
вычисления поправок
за центрировку можно
записать так
де
МK–
величина измеренного направления на
пункт К.В
общем виде без индексов формулу для
вычисления поправок
за центрировку можно
записать так
П оправки
за центрировку вводятся со своим знаком
в измеренные направления на данном
пункте.Выведем
формулу для вычисления поправок
за редукцию. Пусть
с пункта N
производилось наблюдение на визирный
цилиндр V,
проекция которого не совпадает с центром
пункта С.
оправки
за центрировку вводятся со своим знаком
в измеренные направления на данном
пункте.Выведем
формулу для вычисления поправок
за редукцию. Пусть
с пункта N
производилось наблюдение на визирный
цилиндр V,
проекция которого не совпадает с центром
пункта С. Расстояние
e1,
называется линейным
элементом редукции.
Угол Θ1
с вершиной в точке V,
считаемый от направления на центрС
до нулевого направления N
по ходу часовой стрелки, называется
угловым
элементом редукции.
Из рис. видно, что в направление
NV
нужно ввести поправку
Расстояние
e1,
называется линейным
элементом редукции.
Угол Θ1
с вершиной в точке V,
считаемый от направления на центрС
до нулевого направления N
по ходу часовой стрелки, называется
угловым
элементом редукции.
Из рис. видно, что в направление
NV
нужно ввести поправку
а в направление KV
поправку
в направление KV
поправку
В общем виде формулу для вычисления
поправок за
редукцию
можно записать так
общем виде формулу для вычисления
поправок за
редукцию
можно записать так
Поправки за редукцию вычисляются на данном пункте для всех направлений, но вводятся со своим знаком в направления, измеренные на соседних пунктах.
7.
Способы определения элементов
приведения.Величиныe,
e1,
Θ, Θ1необходимые
для вычисления с
и r
называются элементами приведения. Для
их определения чаще всего применяют
графический
способ.
Над центром пункта устанавливают
центрировочный столик, на который
прикрепляют лист бумаги. Затем с помощью
вспомогательного теодолита проектируют
на центрировочный лист центр пункта
C,
ось вращения теодолита Pи
ось визирного цилиндра V.Проектирование
выполняют при двух положениях круга с
трех точек, расположенных так, чтобы
проектирующие плоскости пересекались
под углом 1200.
Стороны треугольников погрешностей
при проектировании точек С
и Р
не должны превышать 0,5 см, а для точки
V
– 1 см. Окончательное положение проекций
точек С, Р
и V
намечают в центре треугольников
погрешностей.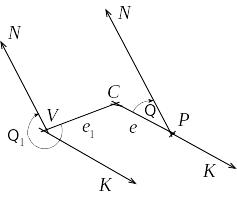 Линейные
элементы приведения CP=е
и VC=е1измеряют
с точностью до 1
мм. Для
определения угловых элементов приведения
Θ
и Θ1,
из точек Р
и V
c помощь визирной линейки прочерчивают
направления на начальный пункт, после
чего углы измеряют транспортиром.Для
контроля прочерчивают направления еще
на один из пунктов K,
измеряют транспортиром углы NPK,
NVKи
сравнивают их с измеренными
теодолитом.Графический способ применяют
в случаях, когда е
и е1небольшие.
Если е
не вмещается на центрировочный лист,
то его измеряют непосредственно
рулеткой, как расстояние между нитью
отвеса, установленного над центром
пункта, и нитью отвеса теодолита. Угол
измеряют непосредственно теодолитом.
Линейные
элементы приведения CP=е
и VC=е1измеряют
с точностью до 1
мм. Для
определения угловых элементов приведения
Θ
и Θ1,
из точек Р
и V
c помощь визирной линейки прочерчивают
направления на начальный пункт, после
чего углы измеряют транспортиром.Для
контроля прочерчивают направления еще
на один из пунктов K,
измеряют транспортиром углы NPK,
NVKи
сравнивают их с измеренными
теодолитом.Графический способ применяют
в случаях, когда е
и е1небольшие.
Если е
не вмещается на центрировочный лист,
то его измеряют непосредственно
рулеткой, как расстояние между нитью
отвеса, установленного над центром
пункта, и нитью отвеса теодолита. Угол
измеряют непосредственно теодолитом.
8. Предварительная обработка триангуляция.После выполнения полевых работ приступают к предварительной обработке триангуляции:1. Проверяют полевые журналы и центрировочные листы. 2. Вычисляют средние значения направлений и составляют сводные ведомости измеренных величин.3. Составляют схему сети с измеренными направлениями и углами. 4.Выполняют предварительное решение треугольников. 5. Вычисляют поправки за центрировку и редукцию. 6. Вычисляют приведенные к центрам направления. 7. Составляют схему сети с приведенными направлениями. 8. Вычисляют угловые невязки и проверяет их допустимость. 9. Делают оценку точности угловых измерений по невязкам треуголь-ников.10.Устанавливает допустимость невязок.
9
 .
Виды условных уравнений в триангуляции.
При
построении триангуляции в целях контроля
и повышения точности кроме необходимых
измеряют избыточные
величины.
Например, в треугольниках измеряют все
три угла, хотя для их решения необходимо
только два. Геодезические сети, имеющие
только необходимые исходные данные,
называются свободными.Если
сеть содержит избыточные исходные
данные, то она несвободная.
Каждое избыточное измерение и избыточное
исходное данное позволяют записать
математическое соотношение между
измеренными величинами, т.е. условное
уравнение.
При создании триангуляции возникают
условия фигур,
горизонтов, сумм, полюсов, сторон,
дирекционных углов и
координат. 1) Условие фигур, заключается
в том, что в любой замкнутой фигуре
сумма уравненных углов должна быть
1800(n–2).
Обозначим
измеренные углы арабскими
цифрами 1,2,3…,
поправки к ним – цифрами
в скобках (1), (2), (3)…,
уравненные значения углов –цифрами
с чертой
.
Виды условных уравнений в триангуляции.
При
построении триангуляции в целях контроля
и повышения точности кроме необходимых
измеряют избыточные
величины.
Например, в треугольниках измеряют все
три угла, хотя для их решения необходимо
только два. Геодезические сети, имеющие
только необходимые исходные данные,
называются свободными.Если
сеть содержит избыточные исходные
данные, то она несвободная.
Каждое избыточное измерение и избыточное
исходное данное позволяют записать
математическое соотношение между
измеренными величинами, т.е. условное
уравнение.
При создании триангуляции возникают
условия фигур,
горизонтов, сумм, полюсов, сторон,
дирекционных углов и
координат. 1) Условие фигур, заключается
в том, что в любой замкнутой фигуре
сумма уравненных углов должна быть
1800(n–2).
Обозначим
измеренные углы арабскими
цифрами 1,2,3…,
поправки к ним – цифрами
в скобках (1), (2), (3)…,
уравненные значения углов –цифрами
с чертой Тогда
условие фигуры ABOзапишется
так
Тогда
условие фигуры ABOзапишется
так
1+(1)+2+(2)+3+(3)–1800 = 0. 1+2+3–1800 = w.
(1)+(2)+(3)+w = 0.Полученное уравнение называется условным уравнением поправок. Здесь w– свободный член (невязка).2) Условие горизонта заключается в том, что сумма уравненных углов, замыкающих горизонт на пункте, должна равняться 3600.
Применительно к рисунку имеем
(3)+(6)+(9)+(12)+(15)+wГ = 0,
wГ = 3+6+9+12+15–3600 – свободный член (невязка).
3)Условие суммзаключается в том, что сумма, уравненных углов, входящих в исходный угол, должна равняться его значению. Условие возникает при построении типовой фигуры «вставка в угол».
Условие сумм для рисунка запишется так

( 2)+(4)
+wS = 0,
2)+(4)
+wS = 0,
Условие сумм можно рассматривать и как условие дирекционных углов, так как B можно выразить черезисходные дирекционные углы:
![]() B
= αBA–
αBC.
B
= αBA–
αBC.
4) Полюсное условие заключается в том, что длина одной и той же стороны, вычисленная двумя независимыми путями по уравненным углам должна иметь в обоих случаях одинаковое значение.
 а)
а)

б)

Все стороны имеют общую точкуО, называемую полюсом. Для перехода к условным уравнениям поправок в уравнении (10) необходимо заменить уравненные углы измеренными с поправками и привести его к линейному виду, разложив в ряд Тейлора, ограничиваясь первыми степенями поправок.



Е
 сли
второе слагаемое умножить и разделить
на sin1,
то его с достаточной точностью можно
заменить значением . Аналогично
мож-но преобразовать и другие
слагаемые.Введем следующие обозначения
сли
второе слагаемое умножить и разделить
на sin1,
то его с достаточной точностью можно
заменить значением . Аналогично
мож-но преобразовать и другие
слагаемые.Введем следующие обозначения
Т
 огда
полюсное условное уравнение поправок
в угловой мере будет иметь вид
огда
полюсное условное уравнение поправок
в угловой мере будет иметь вид
5 )
Условие
сторон (базисов)заключается
в том, что длина одной исходной стороны,
вычисленная по другой исходной стороне
и уравненным углам должна быть равна
известному ее значени
)
Условие
сторон (базисов)заключается
в том, что длина одной исходной стороны,
вычисленная по другой исходной стороне
и уравненным углам должна быть равна
известному ее значени
![]()



6)Условие дирекционных угловзаключается в том, что дирекционный угол одной исходной стороны, вычисленный по дирекционному углу другой исходной стороны и уравненным углам должен быть равен известному его значению
α AB–[3+(3)]+[6+(6)]–[9+(9)]+[12+(12)]–
αСD=0.wα=
αAB
–3 + 6 – 9 + 12 – αСD.–(3)
+ (6) – (9) + (12) + wα
= 0.
AB–[3+(3)]+[6+(6)]–[9+(9)]+[12+(12)]–
αСD=0.wα=
αAB
–3 + 6 – 9 + 12 – αСD.–(3)
+ (6) – (9) + (12) + wα
= 0.
