21. Системы линейных возвратных уравнений первого порядка с постоянными коэффициентами. Их решение для случая двух уравнений с двумя переменными.
22. Устойчивость системы разностных уравнений.
Ситстема разностных уравнений называется устойчивой, если её решение ограничено при любых начальных условиях.
Система уравнений называется неустойчивой, если существует хотя бы один набор начальных условий, для которого её решения не ограничены.
Все решения линейной системы однородной или неоднородной по отношению к свойству устойчивости (асимптотической устойчивости) ведут себя одинаково: либо все устойчивы, либо все неустойчивы. Для нелинейных конечно-разностных уравнений ограниченность и даже стремление к нулю всех его решений еще не гарантирует устойчивости.
Устойчивая система ур-ний называется ассимптотически устойчивой системой, если её решения стремятся к нулевому вектору
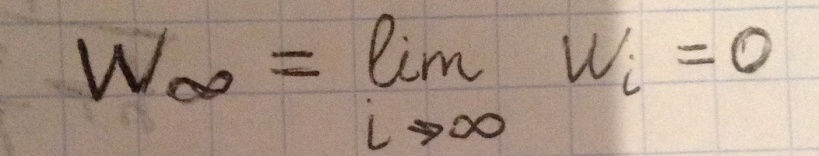
Теорема. Линейная однородная система устойчива тогда и только
тогда, когда все ее решения ограничены при t≥t0.
Следствие теоремы. У устойчивой линейной неоднородной системы все ре-
шения ограничены или неограниченны одновременно при t≥t0.
Теорема. Линейная однородная система асимптотически устойчива
тогда и только тогда, когда все ее решения стремятся к нулю при t→+∞.
Решения системы – это векторные числовые последовательности. Так как они имеют предел, то они ограничены при t≥t0. Из ограниченности всех решений следует устойчивость системы. Кроме того, тривиальное решение является притягивающим с ∆=+∞. Система асимптотически устойчива.
23.Импульсные (когнитивные) модели. Их назначение и параметризация.
Одним из наиболее эффективных инструментов прогнозирования тенденций развития СЭП , в том числе с учетом оказания на них управляющих воздействий, являются когнитивные модели.Когнитивные модели — это разновидность структурно-параметрической формализации* СЭП в виде нагруженного графа, вершинам и дугам которого сопоставляются некоторые параметры.
Вершинам соответствуют существенные факторы, которые определеяют динамику развития исходного процесса. Дуги орграфа отражают непосредственно причинно-следственные отношения между факторами, соотвесвующими соединенным этой дугой вершинам.Дуга идет из вершины, соответствующей причине, в вершину, соответствующую следствию.Параметризация когнитивных моделей:
Структурная составляющая когнитивных моделей дополняется параметрической. К ней прежде всего относятся параметры, дающие описание выбранных факторов в количественной шкале.Предположим, что изменение фактора-причины вызовет спустя некоторое время воздействующее изменений фактора-следствия.Предположим равенство или, в крайнем случае, кратность времени осуществления различного воздействия, что определяет естественую единицу измерения времени, используемую при моделировании и построение моделей с дискретным временем.Воздействия описываются один параметром — интенсивностью воздействия.Интенсивность воздействия изменяется в количественной или в качественной шкале с 3мя уровнями (-1, 0, +1).При использовании количественной шкалы граф называется нагруженным, при использовании качественной шкалы, граф называется знаковым.При использовании качественной шкалы интенсивность воздействия фактора-причины на фактор-следствия ставится в соответствие +1 (а соединяющей их дуге орграфа — знак «+»), если знак изменения фактора-причины совпадает со знаком вызванного им изменения второго фактора-следствия.Если же знаки этих изменений разные, то и интенсивности воздействия, и дуге ставится в соответствие знак «-».Если в орграфе отсутствует дуга, идущая из одной какой-то вершины в другую, то интенсивность соответствующего воздействия считается равной 0.знаковый ориентированный граф называют так же когнитивной картой моделируемого процесса.Путём из вершины А в вершину В орграфа называется непрерывная последовательность дуг одной ориентации, начинающихся в вершине А и заканчивающихся в вершине В.Длина пути равна числу входящих в него дуг. Знак пути определяется как произведение знаков, входящих в него дуг.Как правило орграф модели является сильносвязанным. Это означает, что из любой вершины имеется ориентированный путь в любую другую вершину.