17. Линейные возвратные уравнения второго порядка с постоянными коэффициентами. Характеристическое уравнение и его значение для нахождения решения.

Линейное раностное ур-е 2-го пор-ка с пост коэф имеет вид:

y_i+2 + Py_i+1+Q y_i = o

имеет частное решение y_i = Czⁱ ; С не равно 0

если Cz^{i +2} +Cpz^{i +1}+Cqzⁱ =0

т. е. если z является корнем уравнения:

z² +pz+q=0

Это уравнение называется характеристическим ур-нием линейным разностным уравнением

18. Линейные возвратные уравнения второго порядка с постоянными коэффициентами. Вид решения при действительных корнях характеристического уравнения.

Линейное раностное ур-е 2-го пор-ка с пост коэф имеет вид:

y_i+2 + Py_i+1+Q y_i = o

имеет частное решение y_i = Czⁱ ; С не равно 0

если Cz^{i +2} +Cpz^{i +1}+Cqzⁱ =0

т. е. если z является корнем уравнения:

z² +pz+q=0

Это уравнение называется характеристическим ур-нием линейным разностным уравнением

Далее возможны 3 случая. Мы рассмотрим вид решения при действительных корнях характеристического уравнения.

При дискриминанте D=p²=4q >0 имеет 2 различных действительных корня z1 и z2.

Тогда имеем 2 частных решения ур-ния

Y_1i = C₁z₁ⁱ и Y_2i = C₂z₂ⁱ

Можно доказать, что их линейная комбинация Y_i = C₁z₁ⁱ+C₂z₂ⁱ является общим решением линейного разностного уравнений

пример 1. Числа Фибонначи

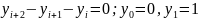
Характерестич. ур-е.

Имеем 2 разн. действит. Корня

19. Линейные возвратные уравнения второго порядка с постоянными коэффициентами. Вид решения при комплексных корнях характеристического уравнения.

Линейное раностное ур-е 2-го пор-ка с пост коэф имеет вид:

y_i+2 + Py_i+1+Q y_i = o

имеет частное решение y_i = Czⁱ ; С не равно 0

если Cz^{i +2} +Cpz^{i +1}+Cqzⁱ =0

т. е. если z является корнем уравнения:

z² +pz+q=0

Это уравнение называется характеристическим ур-нием линейным разностным уравнением

Далее возможны 3 случая. Мы рассмотрим вид решения при комплексных корнях характеристического уравнения:

При дисрименанте D=p²-4q < 0 имеем 2 комплексных сопряженных корня.

Z₁ = а+b₁ = ve ^ip = v (cos альфа + i sin альфа)

z2 = а-b₁ = ve ^ip = v (cos альфа - i sin альфа)

Пример:

y_i+2-2y_i+1+y_i = 0 y0=0, y1=1; 0,1,2,3,4....

Характеристич ур-е:

z² — 2z+1 = (x-1)² = 0

20. Собственные числа и собственные векторы квадратных матриц. Их свойства.

Ненулевой n-мерный вектор x называется собственным вектором матрицы A n-го порядка, соотвествущий собственному числу λ, если

Ax = λx = λEx, где E — единичная матрица

Ax — λEx = (A-λE)x = 0 (1)

Ненулевое решение системы однородных ур-ний (1) существует только если матрица системы вырождения

det (A — λE) = 0 (2)

Решив уравнение (2) находим собственные числа матрицы, подставляя найденное λ в (1) находим соответствующий ему вектор x.

Собственные векторы имеют свойства:

Если x — cобственный вектор, то Cx, где C — const, тоже собственный вектор, соотвествующий λ. Свойства собственных векторов и собственных чисел:

1. Любая линейная комбинация собственных векторов соотвествует одному и тому же собственному числу λ, являющимся собственным вектором с тем же собственным числом

2. Собственные векторы с попарно различными собственными числами линейно независимы

3. Если собственные числа λ1=λ2=λм=λ, то собственному числу λ соответствует не более m линейно-независимых собственных векторов.

4. Если матрица A — треугольная, её главные диагонали являются собственными числами

5)

6)

7)Если x — собственный вектор матрицы A с собственным числом λ, то x является и собственным вектором матрицы A^m c собственным числом λ^m