
- •Исследование; цели, типовые задачи, общенаучные методы исследования.
- •3.Графическая формализация.
- •4. Структурная формализация.
- •Если важно отразить упорядоченность элементов, то надо использовать не множество, а кортеж:
- •5. Структурно-параметрическая формализация.
- •6. Параметрическая формализация. Классификация параметрических моделей.
- •7. Выбор факторов и характеристик, учитываемых в модели. Модели экстраполяции, «вход-выход» и общая модель динамики.
- •8.Кусочно-линейная интерполяция и экстраполяция
- •9.Квадратичная интерполяция и экстраполяция
- •10. Линейная аппроксимация. Метод наименьших квадратов.
- •11.Классификация моделей по временному промежутку, для которого осуществляется моделирование. Модели жизненного цикла и эволюции.
- •12.Конечные разности первого и второго порядка.
- •13.Рекуррентные последовательности и их задание с помощью конечных разностей.
- •14. Разностные уравнения и их виды. Решение разностного уравнения.
- •Решение разностного уравнения:
- •15. Линейные возвратные уравнения. Вид решения однородного и неоднородного возвратного уравнения.
- •16.Линейные возвратные уравнения первого порядка. Уравнения для арифметической и геометрической прогрессий.
- •17. Линейные возвратные уравнения второго порядка с постоянными коэффициентами. Характеристическое уравнение и его значение для нахождения решения.
- •18. Линейные возвратные уравнения второго порядка с постоянными коэффициентами. Вид решения при действительных корнях характеристического уравнения.
- •19. Линейные возвратные уравнения второго порядка с постоянными коэффициентами. Вид решения при комплексных корнях характеристического уравнения.
- •20. Собственные числа и собственные векторы квадратных матриц. Их свойства.
- •21. Системы линейных возвратных уравнений первого порядка с постоянными коэффициентами. Их решение для случая двух уравнений с двумя переменными.
- •22. Устойчивость системы разностных уравнений.
- •23.Импульсные (когнитивные) модели. Их назначение и параметризация.
- •24. Импульсный процесс и правила его развития. Уравнения импульсного процесса.
- •Уравнение импульсного процесса
- •25. Решение уравнений импульсного процесса. Виды устойчивости импульсного процесса.
- •26. Основные понятия дифференциальных уравнений.
- •29. Линейные дифференциальные уравнения первого порядка.
- •30.Однородные дифференциальные уравнения второго порядка с постоянными коэффициентами. Характеристическое уравнение и его значение для нахождения решения.
- •33) Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами.
- •34. Системы линейных однородных дифференциальных уравнений первого порядка с постоянными коэффициентами. Вид решения.
- •35.Неоклассические производственные функции.
- •36. Мультипликативная производственная функция задается выражением
- •37.Эластичность производственной функции. Модель роста выпуска.
- •38.Динамическая модель Кейнса
- •45.Динамическая модель Леонтьева. Условия и уравнения.
- •46.Распределения случайных величин: Бернулли и Пуассона.
- •47.Распределения случайных величин: экспоненциальное и нормальное.
- •49.Теорема Чебышева. Закон больших чисел.
- •50.Центральная предельная (теорема Ляпунова)
- •51. Теорема (интегральная формула) Муавра-Лапласа.
- •52. Понятие о статистической оценке параметров. Числовые характеристики выборочного распределения.
- •53. Точечные оценки и их характеристики. Выборочные среднее и дисперсия.
- •54. Понятие об интервальной оценке параметров. Доверительная вероятность и доверительный интервал.
- •55. Интервальная оценка для математического ожидания.
- •56. Случайные процессы. Основные понятия и характеристики.
- •57. Марковские процессы. Конечные цепи Маркова.
- •Отличие Марковского процесса от Марковской цепи
- •58. Потоки событий. Простейший поток.
35.Неоклассические производственные функции.
Производственная функция – это функция, позволяющая определить максимально возможный объем выпуска продукции при различных сочетаниях и количествах ресурсов.
![]() ,
где
,
где
![]() -
реальный выпуск,
-
реальный выпуск,
![]() -
накопленный запас капитала,
-
накопленный запас капитала,
![]() -
параметр эффективности труда,
-
параметр эффективности труда,
![]() -
труд.Производственная функция называется
неоклассической, если она является
гладкой ( т.е. все частные производственные
непрерывны) и удовлетворяет следующим
условиям:
-
труд.Производственная функция называется
неоклассической, если она является
гладкой ( т.е. все частные производственные
непрерывны) и удовлетворяет следующим
условиям:
1)F(0,L)=F(K,0)=0 при отсутствии одного из ресурсов производства невозможно;
2)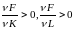 с
ростом производства выпуск растет
с
ростом производства выпуск растет
3)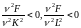 с
ростом ресурсов скорость роста выпуска
замедляется
с
ростом ресурсов скорость роста выпуска
замедляется
4)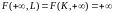 при
неограниченном увеличении одного из
ресурсов выпуск неограниченно растет.
Пример производственной функции,
обладающей такими свойствами является
производственная функция
Кобба-Дугласа
с постоянной отдачей от масштаба:
при
неограниченном увеличении одного из
ресурсов выпуск неограниченно растет.
Пример производственной функции,
обладающей такими свойствами является
производственная функция
Кобба-Дугласа
с постоянной отдачей от масштаба:
![]() ,
где
,
где
![]() -
параметр от нуля до единицы.
-
параметр от нуля до единицы.
Неоклассическая
производственная функция вида
![]() обладает
свойством
обладает
свойством
![]() так
как при отсутствии одного из ресурсов
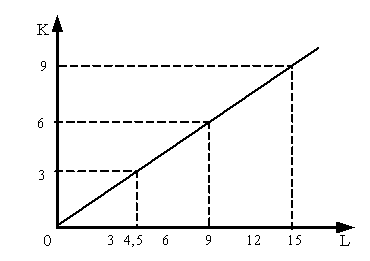
производство невозможно. График
производственной функции В. Леонтьева,
где MRSkl =
0
так
как при отсутствии одного из ресурсов
производство невозможно. График
производственной функции В. Леонтьева,
где MRSkl =
0
36. Мультипликативная производственная функция задается выражением
Производственная
функция называется мультипликативной,
если она задается выражением:
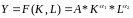
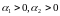 (3),
где А – коэффициент нейтрального
технического прогресса, А>0
(3),
где А – коэффициент нейтрального
технического прогресса, А>0
1)F(0,L)=F(K,0)=0
2)
1).
Мультипликативная функция удовлетворяет
свойству:
 С
ростом объемов ресурсов – выпуск
возрастает.
С
ростом объемов ресурсов – выпуск
возрастает.
2).
Для мультипликативной производственной
функции:
 Может
принимать значения разных знаков,
поэтому одно из свойств неоклассической
модели не выполнено всюду в области
определения функции.
Может
принимать значения разных знаков,
поэтому одно из свойств неоклассической
модели не выполнено всюду в области
определения функции.
3).
![]() Предельный
продукт труда (предельная производительность,
предельная эффективность).
Предельный
продукт труда (предельная производительность,
предельная эффективность).
4).
![]() Предельный
продукт фондов (предельная фондоотдача,
предельная эффективность фондов).
Предельный
продукт фондов (предельная фондоотдача,
предельная эффективность фондов).
5).
В мультипликативной функции средняя
фондоотдача
![]() пропорциональна
средней производительности труда
пропорциональна
средней производительности труда
![]() .
.
(выполнены все свойства).
Предельная
производительность
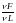 пропорциональна средней производительности
труда
пропорциональна средней производительности
труда
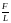 .
.
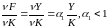 ;
;
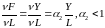
Предельная
фондоотдача
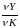 меньше
средней фондоотдачи
меньше
средней фондоотдачи
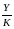
Предельная
производительность труда
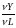 меньше средней производительности
труда
меньше средней производительности
труда
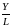 .
С ростом затрат ресурса его отдача
падает5). Параметр
.
С ростом затрат ресурса его отдача
падает5). Параметр
![]() интерпретируется
для мультипликативной функции, как
параметр нейтрального технического
прогресса: с его ростом значения
производственной функции стабилизируются
на некотором уровне.
интерпретируется
для мультипликативной функции, как
параметр нейтрального технического
прогресса: с его ростом значения
производственной функции стабилизируются
на некотором уровне.
Структурные компоненты мультипликативной производственной функции.
1).
Линией уровня на плоскости
![]() называется
геометрическое множество точек плоскости,
для которых производственная функция
показывает тенденции слабой вариации.
называется
геометрическое множество точек плоскости,
для которых производственная функция
показывает тенденции слабой вариации.
2). Линии уровня производственной функции и ее изокванты – это разные понятия, не связанные между собой.
3). Эластичность – это логарифмическая производная фактора:

 .
.
4). Для мультипликативной производственной функции, изокванта является замкнутой линией (кривой второго порядка).
5). По изоквантам производственной функции невозможно установить параметры взаимного замещения ресурсов.
