1. Асимптотическая оценка алгоритма

• Анализ алгоритмов – теоретическое исследование производительности компьютерных программ и потребляемых ими ресурсов.

• Быстродействие – время работы алгоритма, в зависимости от объема входных данных.

• Определяется функцией Т(n), где n – объем входных данных

Виды анализа

• Наихудший случай: T(n) – максимальное время для любых входных данный размера n.

• Средний случай: T(n) – ожидаемое время для любых входных данных размера n.

• Наилучший случай – минимальное время работы.

Асимптотическая оценка

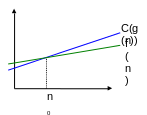
O - нотация: асимптотическая верхняя граница

f (n) = O(g(n)) Þ

($c > 0, n₀> 0 Þ 0 ≤ f (n) ≤ c · g(n), n ≥ n₀)

O(g(n)) = {f (n) : $ c > 0, n₀ > 0 Þ 0 ≤ f (n) ≤ c · g(n), n ≥ n₀}

Пример: 2n² = O(n³)

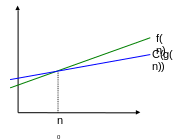
Ω - нотация: асимптотическая нижняя граница

Ω(g(n)) = {f (n) : $c > 0, n₀ > 0 Þ 0 ≤ c · g(n) ≤ f (n), n ≥ n₀}

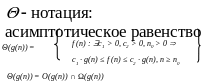
Пример 1

f(n)=1/2n²-3n

Докажем, что g(n)=n² является асимптотической оценкой f(n)

f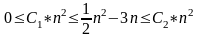 (n)=θ(n²)

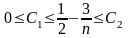
При С₂= 1/2 неравенство будет выполнятся (n→∞) n₀=7, так как n=6 брать нельзя (С₁и С₂>0)

C₁= 1/14, С₂= 1/2 из выражения – 1/2-3/7=1/14. Утверждение верно

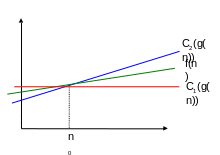
Пример 2

f(n)=6n³

Д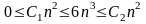 окажем, что g(n)=n² является асимптотической оценкой f(n)

f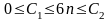 (n)=θ(n²)

П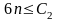 редположение неверно т.к. не выполняется условие

Асимптотические оценки:

θ(1) , θ(log₂n), θ(n), θ(n*log₂n), θ(n2), θ(n3), θ(2ⁿ)

2. Методика оценки не рекурсивных алгоритмов. Пример

for(i=0; i < n-1; i++) {	с1	n
min = i ;	с2	n-1
for ( j = i+1; j <= n-1; j++ )	с3
if (a[ j ] < a [min ])	с4
min = j;	с5
k = a[ i ];	с6	n-1
a[ i ] = a[ min ];	с7	n-1
a[ min ] = k;	с8	n-1
}

= = n + (n-1) + (n-2)…+2 = -1

= (n-1) + (n-2)…+1 =

3. Рекурсивные алгоритмы, построение асимптотической оценки. Пример

Сортировка слиянием

sort(А,p,r) //p - начало массива, r – конец массива T(n)

{

if(p < r) //1

{

q=(p + r)/2; //Вычисляем середину массива 1

sort(А,p,q); //сортируем левую часть T(n/2)

sort(А,q+1,r); //сортируем правую часть T(n/2)

merge(p,q,r); //сливаем два массива в один n

}

}

Дерево рекурсии: T(n) = 2*T(n/2) +cn, с –const, c>0

4. Методика оценки рекурсивных алгоритмов.

Метод итераций

На основании формулы T(n) записываем формулу для меньшего элемента, находящегося в правой части формулы для T(n).

Подставляем правую часть полученной формулы в исходную формулу

Выполняем первые два шага, пока не развернем формулу в ряд без функции T(n)

Оценим полученный ряд на основании арифметической или геометрической прогрессии

Пример:

T(n)=T(n-1)+n, T(1)=1

T(n)=θ(g(n)), g(n)=?

T(n-1)=T(n-2)+(n-1)

T(n-2)=T(n-3)+(n-2)

T(n)= T(n-1)+n=

T(n-2)+(n-1)+n=

T(n-3)+(n-2)+(n-1)+n=…

1+…(n-2)+(n-1)+n=

n*(n+1)

2

T(n)=θ(n²)

Дерево рекурсии - графический метод отображения подстановки соотношения самого в себя

T(n)=2T(n/2)+n²

n²

T(n/2) T(n/2)

n²

(n/2)² (n/2)²

T(n/4) T(n/4) T(n/4) T(n/4)

n² n²

(n/2)² (n/2)² log n (1/2)*n²

(n/4)² (n/4)² (n/4)² (n/4)² (1/4)*n²

T(n)=θ(n²)

Mетод подстановки

1. Догадаться (предложить) о решении

2. Проверить решение с помощью индукции

3. Найти и подставить константы

T (n) = 2T (n/2) + n

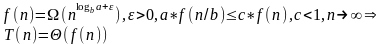
Догадка:

T(n) = (n log n)

Посылка индукции: T(n) ≤ с * n* log n, c>0

Пусть эта оценка верна для n/2

T(n/2) ≤ c*(n/2)*log(n/2)

Подставим ее в исходную формулу для T(n)

T(n) ≤ 2*(c*(n/2)*log(n/2))+n ≤

c*n*log(n/2)+n =

c*n*log n - c*n*log 2 +n =

c*n*log n - c*n +n ≤

c*n*log n

c≥1, n ≥ 2

Основная теорема о рекуррентных оценках

T (n) = aT (n/b) + f (n), a ≥ 1, b > 1, f (n) − (f (n) > 0, n > n0)