Вопрос 9

Вопрос 13

Выделим в потоке струйку, такую малую, что изменением параметров в ее поперечном сечении можно пренебречь и считать их постоянными.

За бесконечно малый промежуток времени Dt участок струйки 1- 2 переместится в положение 1?- 2?.

Применим к этой струйке уравнение энергии, заключающееся в том, что работа сил по перемещению струйки равна приросту кинетической энергии этой струйки.

Известно, что элементарная работа силы определяется выражением

Работа поверхностных сил давления тогда составит

Т. к. в первом сечении направление сил давления совпадает с направлением вектора скорости, а во втором сечении оно противоположно, то      

Заметим, что работа сил давления, действующих по боковым поверхностям струйки равна 0, вследствие ортогональности векторов давления и скорости.

Суммарная работа поверхностных сил определится выражением

Элементарная работа массовых сил (сил веса) определяется изменением потенциальной энергии выделенного элемента массы

Потенциальная энергия массы, заключенной в объеме W определяется выражением

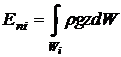
Учитывая, что для несжимаемой жидкости r= const, получим

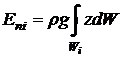
Объем, занимаемый струйкой в начальном и конечном положениях можно представить в виде двух составляющих, рис. 3.1.

Масса жидкости, заключенная в объемах W1 и W2 определится как

Т. к. приток массы в рассматриваемой струйке отсутствует, то M1 = M2 следовательно W1 = W2 Нетрудно заметить, что объем 1?-2 для рассматриваемых положений является общим, тогда   или Это выражение определяет закон сохранения массы для струйки несжимаемой жидкости.

С учетом отмеченного 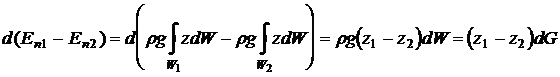где dG = rgdW - элементарный вес жидкости, заключенный в объеме dW. Т. е.

Применяя такой же прием, получим выражение для прироста кинетической энергии струйки

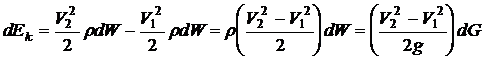
Запишем уравнение баланса энергии Подставляя имеющиеся выражения в данную формулу, получим

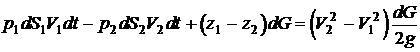
после преобразований, с учетом того, что dW1 = dW2 =dW =dG/g, получаем или, после перегруппирования членов Это выражение и представляет собой уравнение Бернулли для идеальной несжимаемой жидкости. Величина   называется скоростным напором, 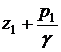  определена ранее как гидростатический напор, а величина 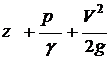  получила название полный напор.

Вопрос 14

где Uср1, и Uср2 – средние скорости в сечениях 1 и 2;

 – потери энергии на преодоление сопротивлений между сечениями 1 и 2.

Уравнение Бернулли устанавливает связь между скоростью движения, давления и геометрическим положением любой точки сечения потока, для которого это написано.

Рассмотрение энергетической и геометрической интерпретации уравнения Бернулли

            С энергетической точки зрения уравнение Бернулли выражает закон сохранения энергии и представляет удельную энергию, отнесенную к единице веса жидкости и подсчитанную относительно произвольно выбранной горизонтальной плоскости. Такая удельная энергия потока состоит из удельной потенциальной энергии   где z – энергия положения,   - энергия давления, и удельной кинетической энергии потока  . С теоретической точки зрения потери энергии   на преодоление сопротивления безвозвратно теряются для потока, т.е. часть механической энергии превращается в тепловую.