Извлечение корня из комплексного числа
Заголовок этого раздела является не совсем точным. Дело в том, что корень из ненулевого комплексного числа однозначно определить нельзя. Он всегда имеет столько значений, какова его степень. Поэтому в данном разделе мы будем говорить о решении уравнения
|
(17.14) |
где
неизвестным служит
,
а
--
известное комплексное число. Но поскольку
в школе решение этого уравнения
записывалось в виде
,
то, не слишком соблюдая математическую
строгость, можно говорить, что мы будем
извлекать корень
-ой
степени из комплексного числа
.
Итак, решаем уравнение (17.14).
Если
,
то
.
Пусть
.
Запишем число
в
тригонометрической форме:
.
Здесь
и
--
известные величины. Запишем неизвестное
число
в
тригонометрической форме:
.
Здесь
и
--
неизвестны. По формуле Муавра
Таким образом,
Если
два комплексных числа равны, то их модули
должны быть равны. Поэтому
.
В этом соотношении
и
--
положительные числа, следовательно
,
где справа стоит обычный арифметический
корень из положительного числа.
Если
два комплексных числа равны, то аргументы
у них могут различаться только на
величину, кратную
.
Поэтому
,
.
Отсюда находим, что
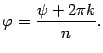
В итоге получили:
|
(17.15) |
Значения
,
отличные от указанных в этой формуле,
дадут те же значения
,
которые можно получить при
