8) Однородные системы линейных уравнений: свойства их решений. Фундаментальная система решений

Однородная система линейных уравнений AX = 0 всегда совместна. Она имеет нетривиальные (ненулевые) решения, если r = rank A < n.

Для однородных систем базисные переменные (коэффициенты при которых образуют базисный минор) выражаются через свободные переменные соотношениями вида:

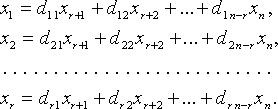
Тогда n - r линейно независимыми вектор-решениями будут:

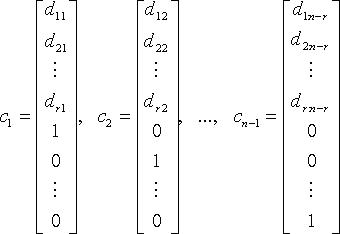
а любое другое решение является их линейной комбинацией. Вектор-решения 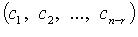образуют нормированную фундаментальную систему.

В линейном пространстве множество решений однородной системы линейных уравнений образует подпространство размерности n - r; - базис этого подпространства.

Фундаментальной системой решений однородного линейного дифференциального уравнения называется упорядоченный набор из n линейно независимых решений уравнения.

Иными словами любые n линейно независимых решений   y₁(x), y₂(x),..., y_n(x) уравнения y⁽ⁿ⁾ + a_n-1(x)y^{(n - 1)} + ... + a₁(x)y' + a₀(x)y = 0 образуют фундаментальную систему решений.

 

Доказано, что у однородного линейного дифференциального уравнения с непрерывными коэффициентами существует фундаментальная система решений.

Пусть задана некоторая линейно независимая система n векторов из R_n:

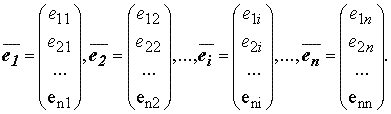
И пусть функции   y₁(x), y₂(x),..., y_n(x) — решения линейного однородного уравнения с начальными условиями:

Функции y₁(x), y₂(x),..., y_n(x) образуют фундаментальную систему решений линейного однородного уравнения.  

9. Линейные пространства

Определение. Линейным пространством L = {a,b,c,…}называется множество, относительно элементов которого определены операции сложения и умножения на число, причем результаты этих операций принадлежат этому же множеству (говорят, что L замкнуто относительно операций сложения и умножения на число): .

(Элементы линейных пространств также будем называть векторами)

Для эти операции удовлетворяют следующим условиям:

1. a + b = b + a (коммутативность сложения).

2. (a + b) + c = a + (b + c) (ассоциативность сложения).

3. .

4.

5. 1·а = а.

6.

7. (α + β)а = αа + βа (дистрибутивность).

8. α(а + b) = αa + αb (дистрибутивность).

Перечисленные свойства, обычно, называют аксиомами. Имеют место теоремы:

Теорема 1. Нулевой элемент – единственен.

{От противного: 0₁,0₂; 0₁+0₂=0₁ и 0₂+0₁=0₂ (акс. (3)). Из акс.(1) следует: 0₁=0₂}

Теорема 2. противоположный элемент – единственен.

{Пусть для }

Теорема 3. 0·а = 0.

{ }

Теорема 4.

{ }

Линейно зависимые и линейно независимые системы элементов.

Определение 1. Сумма называется линейной комбинацией элементов а₁, а₂,…,а_n с коэффициентами λ_k .

Определение 2. Система элементов линейного пространства {a₁,…,a_n} называется линейно зависимой, если найдутся коэффициенты λ₁,…,λ_n не все равные нулю, линейная комбинация с которыми равна нулю, т.е.

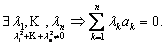
Определение 3. Система элементов линейного пространства {a₁,…,a_n} называется линейно

независимой, если ее линейная комбинация равна нулю только с нулевыми коэффициентами:

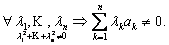
Имеют место несколько простых утверждений.

Теорема 1 (необходимое и достаточное условие линейной независимости). a₁,…,a_n – линейно зависима когда хотя бы один из элементов является линейной комбинацией остальных.

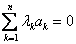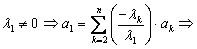{1.(необходимость: {a_k} – л.з. ): . Пусть, для определенности, а₁ – линейная комбинация остальных.

2.(достаточность: a_m – л.к.): }

Теорема 2. Если один из элементов системы равен нулю, то вся система линейно зависима.

{ }

Теорема 3. Если подсистема линейно зависима, то и вся система линейно зависима.

{ }