
- •Матрицы: основные определения, операции над матрицами, их свойства
- •Определители квадратных матриц и их свойства
- •Обратная матрица: определение, метод нахождения
- •Матричные уравнения. Решение матричных уравнений методом обратной матрицы
- •Системы линейных уравнений. Решение систем линейных уравнений методом Крамера, методом обратной матрицы, методом Гауса
- •Ранг матрицы Определение ранга матрицы
- •Вычисление ранга матрицы с помощью миноров
- •Вычисление ранга матрицы с помощью элементарных преобразований
- •Теорема Кронекера-Капелли
- •8) Однородные системы линейных уравнений: свойства их решений. Фундаментальная система решений
- •Линейные пространства
- •Линейно зависимые и линейно независимые вектора
- •Базис линейного пространства, разложение вектора по базису
- •Комплексные числа: определение, операции, геометрическая интерпретация
- •Тригонометрическая форма записи комплексного числа, формула Муавра, извлечение корней из комплексных чисел
- •Извлечение корня из комплексного числа
Обратная матрица: определение, метод нахождения
Матрица В называется обратной для матрицы А, если для них выполняются соотношения А·В = В·А = E. Для обратной матрицы принято обозначение А-1. Эту запись не следует понимать как степень с отрицательным показателем, действие деления для матриц не определено. Это просто обозначение и не более того.
Алгоритм нахождения обратной матрицы
Записать в таблицу для решения систем уравнений методом Гаусса матрицу А и справа (на место правых частей уравнений) приписать к ней матрицу Е.
Используя преобразования Жордана, привести матрицу А к матрице, состоящей из единичных столбцов; при этом необходимо одновременно преобразовать матрицу Е.
Если необходимо, то переставить строки (уравнения) последней таблицы так, чтобы под матрицей А исходной таблицы получилась единичная матрица Е.
Записать обратную матрицу А-1, которая находится в последней таблице под матрицей Е исходной таблицы.
Матричные уравнения. Решение матричных уравнений методом обратной матрицы
Матричные уравнения могут иметь вид:
АХ = В, ХА = В, АХВ = С,
где А,В,С — задаваемые матрицы, Х- искомая матрица.
Матричные уравнения решаются с помощью умножения уравнения на обратные матрицы.
Например, чтобы
найти матрицу
![]() из
уравнения
из
уравнения
![]() ,
необходимо умножить это уравнение на
,
необходимо умножить это уравнение на
![]() слева.
слева.
Тогда:![]()
Следовательно, чтобы
найти решение
уравнения
,
нужно найти обратную матрицу
и умножить ее на матрицу
![]() ,
стоящие в правой части уравнения.
,
стоящие в правой части уравнения.
Аналогично решаются другие уравнения.
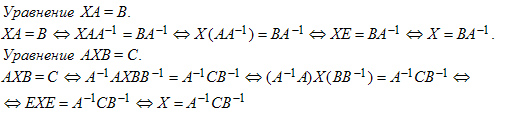
Системы линейных уравнений. Решение систем линейных уравнений методом Крамера, методом обратной матрицы, методом Гауса
Обозначим через
![]() любое
из множеств
любое
из множеств
![]() или
или
![]() .
.
Системой линейных
уравнений
(л.у.) над
называется
совокупность (набор) из нескольких
уравнений от одного и того же набора
переменных (неизвестных)
![]() :
:
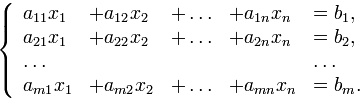
Здесь числа
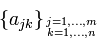 и
и
![]() —
из
;
они называются коэффициентами
системы. Первый
индекс у коэффициента
—
из
;
они называются коэффициентами
системы. Первый
индекс у коэффициента
![]() отвечает
за номер уравнения, а второй — за номер
переменной. Относительно числа
отвечает
за номер уравнения, а второй — за номер
переменной. Относительно числа
![]() уравнений
не делается ни какого предположения:
оно может быть меньше, больше или равно
числу переменных
уравнений
не делается ни какого предположения:
оно может быть меньше, больше или равно
числу переменных
![]() .
Если
.
Если
![]() то
система называется переопределенной.
Решением
системы уравнений
называется любой набор значений
переменных
то
система называется переопределенной.
Решением
системы уравнений
называется любой набор значений
переменных
![]() ,
обращающий каждое из уравнений в истинное
равенство. Система называется совместной
если она имеет хотя бы одно решение и
несовместной
в противном случае.
,
обращающий каждое из уравнений в истинное
равенство. Система называется совместной
если она имеет хотя бы одно решение и
несовместной
в противном случае.
!
Можно доказать (см. результаты НИЖЕ ), что все возможности для произвольной системы ограничиваются следующими вариантами:
1. система совместна и имеет единственное решение;
2. cистема совместна и имеет бесконечное множество решений;
3. cистема несовместна.
Метод Крамера применяется для решения систем линейных алгебраических уравнений (СЛАУ), в которых число неизвестных переменных равно числу уравнений и определитель основной матрицы отличен от нуля. В этой статье мы разберем как по методу Крамера находятся неизвестные переменные и получим формулы. После этого перейдем к примерам и подробно опишем решение систем линейных алгебраических уравнений методом Крамера.
Вычисляем
определитель основной матрицы системы
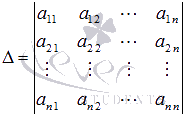 и
убеждаемся, что он отличен от нуля.
и
убеждаемся, что он отличен от нуля.
Находим
определители
 которые
являются определителями матриц,
полученных из матрицы А
заменой k-ого
столбца (k = 1,
2, …, n) на
столбец свободных членов.
которые
являются определителями матриц,
полученных из матрицы А
заменой k-ого
столбца (k = 1,
2, …, n) на
столбец свободных членов.
Вычисляем
искомые неизвестные переменные x1,
x2,
…, xn
по формулам
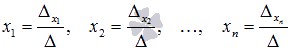 .
.
Выполняем проверку результатов, подставляя x1, x2, …, xn в исходную СЛАУ. Все уравнения системы должны обратиться в тождества. Можно также вычислить произведение матриц A ⋅ X, если в результате получилась матрица, равная B, то решение системы найдено верно. В противном случае в ходе решения была допущена ошибка.
Метод обратной матрицы (Матричный метод) решения систем линейных алгебраических уравнений с ненулевым определителем основной матрицы состоит в поиске матрицы, обратной к основной матрице, и умножению ее на матрицу свободных членов.
Пусть
для матрицы А
порядка n
на n
существует обратная матрица
![]() .
Умножим обе части матричного уравнения
.
Умножим обе части матричного уравнения
![]() слева
на
(порядки
матриц A ⋅
X и В
позволяют произвести такую операцию,
смотрите статью операции
над матрицами, свойства операций).
Имеем
слева
на
(порядки
матриц A ⋅
X и В
позволяют произвести такую операцию,
смотрите статью операции
над матрицами, свойства операций).
Имеем
![]() .
Так как для операции умножения матриц
подходящих порядков характерно свойство
ассоциативности, то последнее равенство
можно переписать как
.
Так как для операции умножения матриц
подходящих порядков характерно свойство
ассоциативности, то последнее равенство
можно переписать как
 ,
а по определению обратной матрицы
,
а по определению обратной матрицы
![]() (E
– единичная матрица порядка n
на n),
поэтому
(E
– единичная матрица порядка n
на n),
поэтому
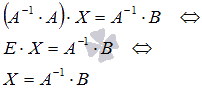 Таким
образом, решение
системы линейных алгебраических
уравнений по матричному методу
определяется равенством
Таким
образом, решение
системы линейных алгебраических
уравнений по матричному методу
определяется равенством
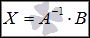 .
Другими словами, решение СЛАУ находится
с помощью обратной матрицы
.
Мы
знаем, что квадратная матрица А
порядка n
на n
имеет обратную матрицу
только
тогда, когда ее определитель не равен
нулю. Следовательно, СИСТЕМУ n
ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ С n
НЕИЗВЕСТНЫМИ МОЖНО РЕШАТЬ МАТРИЧНЫМ
МЕТОДОМ ТОЛЬКО ТОГДА, КОГДА ОПРЕДЕЛИТЕЛЬ
ОСНОВНОЙ МАТРИЦЫ СИСТЕМЫ ОТЛИЧЕН ОТ
НУЛЯ.
.
Другими словами, решение СЛАУ находится
с помощью обратной матрицы
.
Мы
знаем, что квадратная матрица А
порядка n
на n
имеет обратную матрицу
только
тогда, когда ее определитель не равен
нулю. Следовательно, СИСТЕМУ n
ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ С n
НЕИЗВЕСТНЫМИ МОЖНО РЕШАТЬ МАТРИЧНЫМ
МЕТОДОМ ТОЛЬКО ТОГДА, КОГДА ОПРЕДЕЛИТЕЛЬ
ОСНОВНОЙ МАТРИЦЫ СИСТЕМЫ ОТЛИЧЕН ОТ
НУЛЯ.
Метод Гаусса прекрасно подходит для решения систем линейных алгебраических уравнений (СЛАУ). Он обладает рядом преимуществ по сравнению с другими методами:во-первых, нет необходимости предварительно исследовать систему уравнений на совместность; во-вторых, методом Гаусса можно решать не только СЛАУ, в которых число уравнений совпадает с количеством неизвестных переменных и основная матрица системы невырожденная, но и системы уравнений, в которых число уравнений не совпадает с количеством неизвестных переменных или определитель основной матрицы равен нулю; в-третьих, метод Гаусса приводит к результату при сравнительно небольшом количестве вычислительных операций.
Пусть
нам требуется решить систему из n
линейных алгебраических уравнений с n
неизвестными переменными вида
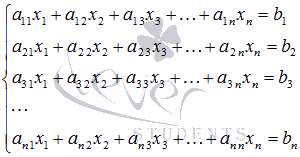 ,
и пусть определитель ее основной матрицы
отличен от нуля.
Будем считать,
что
,
и пусть определитель ее основной матрицы
отличен от нуля.
Будем считать,
что
![]() ,
так как мы всегда можем этого добиться
перестановкой местами уравнений системы.
Исключим неизвестную переменную x1
из всех уравнений системы, начиная со
второго. Для этого ко второму уравнению
системы прибавим первое, умноженное на
,
так как мы всегда можем этого добиться
перестановкой местами уравнений системы.
Исключим неизвестную переменную x1
из всех уравнений системы, начиная со
второго. Для этого ко второму уравнению
системы прибавим первое, умноженное на
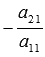 ,
к третьему уравнению прибавим первое,
умноженное на
,
к третьему уравнению прибавим первое,
умноженное на
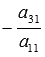 ,
и так далее, к n-ому
уравнению прибавим первое, умноженное
на
,
и так далее, к n-ому
уравнению прибавим первое, умноженное
на
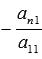 .
Система уравнений после таких
преобразований примет вид
.
Система уравнений после таких
преобразований примет вид
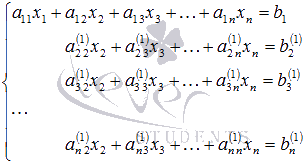 где
где
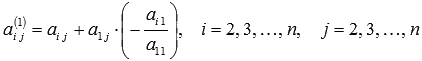 ,
а
,
а
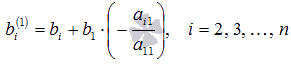 .
К
такому же результату мы бы пришли, если
бы выразили x1
через другие неизвестные переменные в
первом уравнении системы и полученное
выражение подставили во все остальные
уравнения. Таким образом, переменная
x1
исключена из всех уравнений, начиная
со второго.
Далее действуем
аналогично, но лишь с частью полученной
системы, которая отмечена на
рисунке
.
К
такому же результату мы бы пришли, если
бы выразили x1
через другие неизвестные переменные в
первом уравнении системы и полученное
выражение подставили во все остальные
уравнения. Таким образом, переменная
x1
исключена из всех уравнений, начиная
со второго.
Далее действуем
аналогично, но лишь с частью полученной
системы, которая отмечена на
рисунке
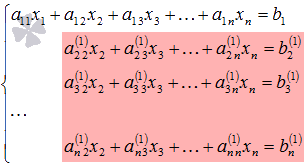 Будем
считать, что
Будем
считать, что
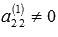 (в
противном случае мы переставим местами
вторую строку с k-ой,
где
(в
противном случае мы переставим местами
вторую строку с k-ой,
где
![]() ).
Приступаем к исключению неизвестной
переменной x2
из всех уравнений, начиная с третьего.
Для
этого к третьему уравнению системы
прибавим второе, умноженное на
).
Приступаем к исключению неизвестной
переменной x2
из всех уравнений, начиная с третьего.
Для
этого к третьему уравнению системы
прибавим второе, умноженное на
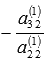 ,
к четвертому уравнению прибавим второе,
умноженное на
,
к четвертому уравнению прибавим второе,
умноженное на
 ,
и так далее, к n-ому
уравнению прибавим второе, умноженное
на
,
и так далее, к n-ому
уравнению прибавим второе, умноженное
на
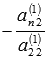 .
Система уравнений после таких
преобразований примет вид
.
Система уравнений после таких
преобразований примет вид
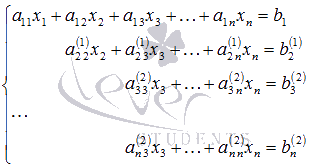 где
где
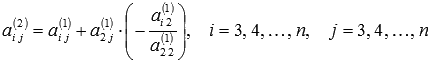 ,
а
,
а
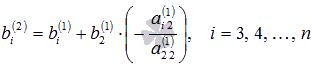 .
Таким образом, переменная x2
исключена из всех уравнений, начиная с
третьего.
Далее приступаем к
исключению неизвестной x3,
при этом действуем аналогично с отмеченной
на рисунке частью системы
.
Таким образом, переменная x2
исключена из всех уравнений, начиная с
третьего.
Далее приступаем к
исключению неизвестной x3,
при этом действуем аналогично с отмеченной
на рисунке частью системы
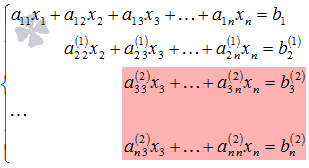 Так
продолжаем прямой ход метода Гаусса
пока система не примет вид
Так
продолжаем прямой ход метода Гаусса
пока система не примет вид
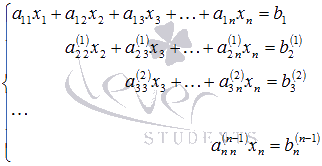 С
этого момента начинаем обратный ход
метода Гаусса: вычисляем xn
из последнего уравнения как
С
этого момента начинаем обратный ход
метода Гаусса: вычисляем xn
из последнего уравнения как
 ,
с помощью полученного значения xn
находим xn-1
из предпоследнего уравнения, и так
далее, находим x1
из первого уравнения.
,
с помощью полученного значения xn
находим xn-1
из предпоследнего уравнения, и так
далее, находим x1
из первого уравнения.
