Задача к1

По заданным в декартовых координатах в табл.4 уравнениям движения точки x = x(t) , y = y(t) найти вид её траектории.

Для заданного момента времени t₁ =1с определить :

- положение точки;

- скорость и ускорение точки;

Таблица 4

П е р в а я ц и ф р а ш и ф р а
	0	x = 4sin(t ⁄6)	3	x = 4 − 2t	7	x = 12 cos(t ⁄6)
	1	x = 3 − 6sin(t ⁄6)	4	x = 2t + 4	8	x = 6cos(t ⁄6) − 2
	2	x = 3sin(t ⁄6) − 2	5	x = − 2t	9	x = 4 − 8cos(t ⁄6)
			6	x = 2t + 2
Вторая цифра шифра	0	y = 4 − 9 cos(t ⁄6)	y = t 2 − 2		y = − 4 cos(t ⁄3)
	1	y = 2 − 3 cos(t ⁄3)	y = 8 cos(t ⁄4)		y = 10 sin(t ⁄6)
	2	y = 4 − 6 cos2(t ⁄6)	y = 4 + 2 t 2		y = 12 sin2(t ⁄6)
	3	y = 12 cos(t ⁄6)	y = 2 (t +1) 2		y = 2 − 4 sin(t ⁄6)
	4	y = 9 cos(t ⁄3) + 5	y = 2 + 2 sin(t ⁄4)		y = 8 + 12 sin(t ⁄3)
	5	y = − 10 cos(t ⁄6)	y = 3 t 2 − 2		y = 3 sin(t ⁄6)
	6	y = 8 cos(t ⁄6) − 3	y = 3 − 4 cos(t ⁄4)		y = 6 sin2(t ⁄6) − 7
	7	y = − 9 cos2(t ⁄6)	y = 3 − 4cos(t ⁄4)		y = 6 cos(t ⁄3)
	8	y = 6 cos(t ⁄3) − 4	y = 2 t 3		y = 4 − 9 sin(t ⁄6)
	9	y = 2 − 2 cos(t ⁄6)	y = 2 sin(t ⁄4)		y = 8 cos(t ⁄3) + 6

Указания. К1 – задача на определение кинематических характеристик движения точки [1, с.99-110] .

В задаче требуется по заданным уравнениям движения точки найти и изобразить её положение на координатной плоскости в момент времени t = t₁ . Следует также построить соответствующие этому моменту времени векторы скорости и ускорения точки.

Образец выполнения

Условия задачи. Даны уравнения движения точки:

x =  2 cos(t ⁄4) + 3, y = 2 sin(t ⁄8) 1 ( х , y – в cм , t – в с ). (1)

Определить положение точки, а также скорость и ускорение точки в момент времени t₁ = 1 c.

Решение. Найдем положение точки в момент времени с . Для этого вычисляем значения координат:

1,59 см ,

– 0,24 см

На рис.4 этому положению соответствует точка М .

Находим выражения для проекций вектора v скорости точки на координатные оси, используя известные формулы кинематики:

,

(здесь и далее точки над переменными означают дифференцирование по времени) .

Находим модуль вектора скорости: .

Вычисляем значения при с :

1,11 см/c ,

0,73 см/c ,

1,33 см/с .

Аналогично находим проекции вектора а ускорения точки на координатные оси и модуль ускорения [1 c.103]:

,

,

.

Значения, соответствующие с будут:

0,87 см/c² ,

– 0,12 см/c² ,

0,88 см/c² .

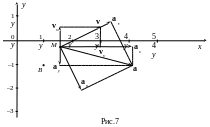
Ответ: М(1,59; -0,24) - положение точки; v(1,11; 0,73), v = 1,33 см/с - скорость; a(0,87; -0,12), a = 0,88 см/с² - ускорение.