Вариант 2
Задание 1. На станции метро в вагон вошли 5 человек. Каждый из них может с одинаковой вероятностью выйти на любой из восьми станций. Найти вероятность того, что
а) все они выйдут на одной станции;
б) три человека выйдут на одной станции.
Задание 2. а) В круг радиуса R вписан правильный треугольник. Найти вероятность того, что точка, брошенная в этот круг, попадет в треугольник?
б) В шар радиуса R вписан куб. Найти вероятность того, что точка, выбранная наугад внутри шара, окажется внутри куба.
Задание 3. Три стрелка стреляют по мишеням. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,7, для второго - 0,85, для третьего – 0,75. Найти вероятность того, что при трех независимых выстрелах в мишень
а) попадут все стрелки;
б) не попадет ни один стрелок;
в) попадет только один из стрелков;
г) попадет хотя бы один стрелок;
д) попадут только два стрелка.
Задание 4. Вероятности того, что во время работы компьютера произойдет сбой жесткого диска, оперативной памяти и монитора относятся как 3:2:5. Вероятности обнаружения сбоя жесткого диска, оперативной памяти и монитора соответственно равны 0,8, 0,9 и 0,7. Найти вероятность того, что
а) возникший в компьютере сбой будет обнаружен;
б) обнаруженный сбой произошел в жестком диске.
Задание 5. Дано распределение дискретной случайной величины Х.
1) Найти математическое ожидание, дисперсию, среднее квадратическое отклонение.
2) Построить функцию распределения и ее график.
Х |
0,2 |
0,5 |
0,6 |
0,8 |
Р |
0,1 |
0,5 |
0,2 |
0,2 |
Задание
6. Дана
плотность
распределения случайной величины
.
Требуется найти: а) неизвестный параметр
;
б) функцию распределения случайной величины ;
в) вероятность того, что случайная величина примет значение из интервала ;
г) математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины .
Дано:
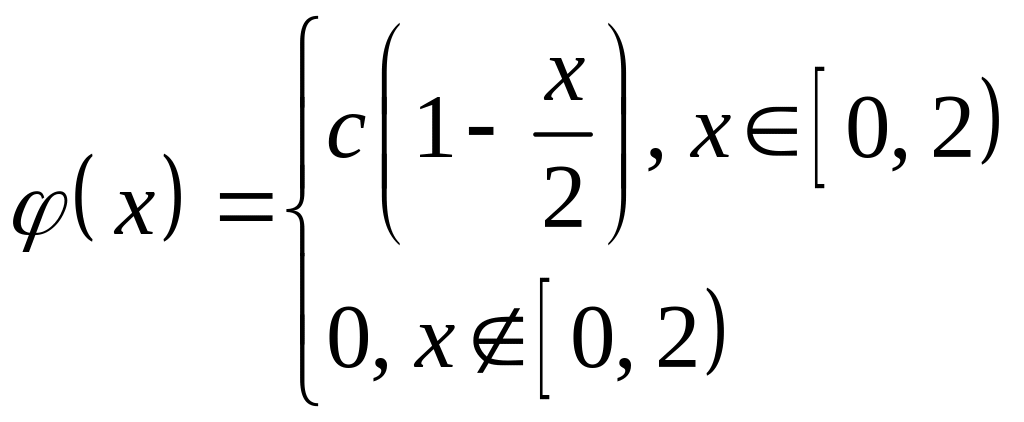
Задание 7. Станок-автомат штампует детали. Вероятность того, что изготовленная деталь окажется бракованной, равна 0,01. Найти вероятность того, что среди 200 деталей окажется
а) не более четырех бракованных;
б) более четырех бракованных.
Задание
8. Длина
изготавливаемой автоматом детали
представляет собой случайную величину,
распределенную по нормальному закону
с параметрами
=
15 см,
=
0,2 см. Найти вероятность брака, если
допустимые размеры детали должны быть
15
0,3 см. Какую точность длины изготавливаемой
автоматом детали можно гарантировать
с вероятностью 0,97?
Задание 9. В страховой компании n клиентов. Страховой взнос каждого из них составил s ден. ед. При наступлении страхового случая, вероятность которого, по оценке экспертов, равна p, страховое возмещение равно с ден. ед. Какова вероятность того, что страховая компания окажется к концу года в убытке?
n = 2000, p = 0,005, s = 5, с = 500.
Задание 10. Вероятность изготовления детали высшего сорта на данном станке равна 0,8. Найти вероятность того, что среди наугад взятых 100 деталей окажется:
а) 70 деталей высшего сорта;
б) не менее 80 деталей высшего сорта.
Задание 11. Станок-автомат штампует валики. Для выборки объема 12 выборочный средний диаметр валиков составил 10 мм, а их среднее квадратическое отклонение – 2 мм. Предполагается, что диаметры валиков распределены нормально. Определить доверительный интервал, с надежностью 0,9 содержащий:
а) математическое ожидание диаметра валика во всей генеральной совокупности;
б) дисперсию диаметра валика.
Задание 12. Ожидается, что добавление специальных веществ уменьшает жесткость воды, которая подчиняется нормальному закону распределения. Оценки жесткости воды до и после добавления специальных веществ по 40 и 50 пробам соответственно показали средние значения жесткости, равные 4 и 3,8 градуса. Дисперсия измерения в обоих случаях предполагается равной 0,25 град2. Подтверждают ли эти результаты ожидаемый эффект (уровень значимости принять равным 0,05)?