Надежность системы с облегченным резервом.
Облегченный резерв - резерв, который содержит один или несколько резервных элементов, находящихся в менее нагруженном состоянии, чем основной элемент.
Считаем, что подключение резерва к цепям питания применяется для прогрева и удержания требуемых значений параметров. Резервные элементы имеют некоторую интенсивность отказов (не = 0), (ʎр не =0). Система включает однонадежные основные и резервные элементы. Элементы невосстанавливаемые. Работа системы:
0
Отказ осн.эл. t
Начало работы τ Работа рез.эл.
Рассмотрим события : А-безотказная работа системы на [0, t], А1 – безотказная работа осн.эл. на [0, t], А2 – отказ осн.эл. в момент τ< t, безотказ. работа рез.эл. на [t- τ]
А = А1+А2
Вероятность безот.работы системы за наработку от 0 до t:
р(А)= р(А1)+р(А2)
р(А)= рс(t), р(А1) = р0(t), р(А2) = рр(t).
А2 = А21*А22*А23, где А21 – отказ осн.эл. при наработке τ(-момент включения рез.эл. в работу),
А22 – безотказ.работа рез.эл. до τ,
А23 – безотк.работа рез.эл. на [τ,t],
р(А2) = р(А21)*р(А22)*р(А23)
Интервал [τ, τ + dτ] . Определяем вероятность отказа на этом интервале. Плотность распределения отказов осн.эл.: f0 = (- dp0(τ)) / dτ.
Вероятность безотк.работы до момента отказа осн.эл.: рр(τ) = р(А22) .
Вероятность безотк.работы до момента включения до t: рр(t - τ) = р(А23).
Вероятность безотк.работы осн.эл. на интервале dτ: р = рр(τ)* рр(t - τ)* f0(τ)dτ (выражает безотк.работу на бесконечно малом интервале).
Производим инегрирование данного выражения на [0, t]. Тогда вероятность безотк.работы системы с ненагруженным резервом :
рс(t)=
рр(t) +
Если система состоит из n – равнонадежных элементов:
рс(t)=
р (n-1)с(t)
+
Учитывая, что ʎ распространяется по экспоненциальному закону:
рр(τ) = exp(-ʎр * τ), рр(t - τ) = exp(-ʎраб *(t - τ)), f0(τ) = ʎраб * exp (-ʎраб * τ), p0(t)= exp(-ʎраб * t),
где ʎраб – интенсивность отказов эл. в рабочем режиме, ʎр - интенсивность отказов в режиме резерва.
рс(t)= exp(-ʎр
* τ) (1+
)
Если система состоит из n – равнонадежных элементов:
рс(t)= р (n-1)с(t)+
exp(-ʎраб * t)(1-
exp(-ʎр * t))
n-1, где
Средняя наработка до отказа системы из n элементов:
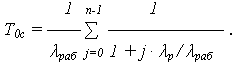
Надежность системы со скользящим резервом.
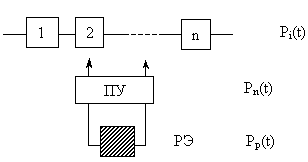
При скользящем резервировании резервный элемент может быть включен взамен любого из отказавших элементов основной системы.
Основная система – n элементов.Резервная группа – m элементов. Обычно m < n, т. е. число резервных элементов (РЭ) меньше числа основных (ОЭ), поэтому скользящее резервирование считается активным с дробной кратностью.
Отказ системы наступает в случае, когда число отказавших основных элементов превысит число резервных. Примером может служить организация линий связи, когда имеется одна резервная линия на несколько основных (в практике, трех). Допущение: РЭ и элементы основной системы равнонадежны и РЭ не может отказать до момента его включения в работу.
A =
{БР системы за наработку (0,
t )};
A1 =
{БР всех элементов
основной системы за наработку (0,
t )};
A2 =
{БР при условии, что отказал один элемент
из 
при
< t,
переключающее устройство работоспособно
– включение РЭ и БР его на
интервале (t -
)}.
Событие
A выполняется в результате выполнения
одного из событий A1 или A2 :
A = A1
A2.
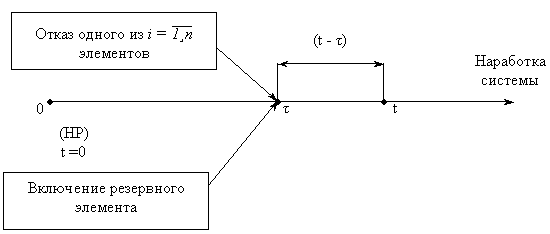
ВБР системы за наработку (0, t ) равна: P( A ) = P( A1 ) + P( A2 ) , где P( A ) = Pс ( t ); P( A1 ) = P1 ( t ) = P0c ( t ) = Pn ( t ) – ВБР основной системы (ОС) к моменту t, где P1 ( t ) = … = Pn ( t ) = P ( t ) – ВБР каждого из элементов; P( A2 ) = P2 ( t ) – ВБР для события A2. Для определения вероятности P( A2 ), рассмотрим событие A2: A121 = {отказ одного (первого) из элементов ОС при < t}; A122 = {БР переключающего устройства (ПУ) до наработки – момента включения РЭ}; A123 = {БР РЭ после включения его в работу, т. е. на интервале (t - )}.
P(A12) = P(A121) · P(A122) · P(A123) . Индекс 1 – отказ 1 элемента ОС
Выделяется бесконечно малый интервал [ , + d ] и определяется ВО ОЭ в интервале [ , + d ]:
f( )d = - dP( ) / d .
ВБР ПУ до момента отказа одного из элементов ОС равна Pп( ); ВБР РЭ с момента его включения, т. е. за интервал (t - ): Pр ( t - ).
Поскольку
событие A2,
заключающееся в БР системы, подразумевает
БР при отказе любого из n элементов ОС,
то его можно рассматривать, как
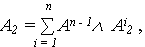
An – 1 – событие, заключающееся в БР оставшихся (n – 1) элементов ОС; Ai2 – БР системы при отказе i-го элемента (не только первого) ОС.
где P(An –
1)
= Pn –
1( t ) .
Поэтому
ВБР системы при отказе
элемента
ОС выражается:
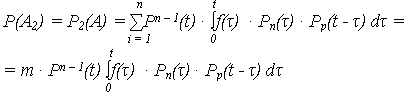
ВБР
системы со скользящим резервом
определяется:
р(t)
– ВБР для каждого элемента.