- •Мощность, излучаемая элементарным электрическим излучателем. Сопротивление излучения. Эквивалентная схема излучателя.
- •Принцип перестановочной двойственности уравнений Максвелла.
- •23. Элементарный магн излучатель. Опред векторов поля, создаваемого излучателем в окруж прост-ве. Анализ структуры поля. Д-ма направленности. Физ модель.
- •24. Элемент Гюйгенса. Направленные свойства.
- •25. Плоские волны в однородной изотропной среде без потерь. Опр векторов поля. Осн св-ва. Фаз скорость. Хар-ое сопрот. Коэф-нт распространения. Длина волны.
- •26. Плоские волны в средах с потерями. Определение векторов поля. Основные свойства. Определения коэффициентов распространения и затухания, понятие дисперсии.
- •27.Математическая запись векторов поля плоской волны, распространяющейся под углом к осям координат.
- •28.Поляризация векторов поля. Виды поляризации.
- •29. Волновые явления на границе раздела двух сред при падении норм- поляриз плоской волны. Законы Снел. Коэфф Френеля.
- •30. Волновые явления на границе раздела двух сред при падении параллельно- поляризованной плоской волны. Законы Снеллиуса. Коэффициенты Френеля.
- •32. Полное внутреннее отражение при падении плоской волны на границу раздела двух сред. Структура поля. Основные свойства. Понятнее о направ волнах типа н и е.
- •33. Падение плоской волны на поверхность идеального металла.
- •34. Принцип действия диэлектрического и металлического волноводов.
- •35. Падение плоской волны на границу поглощающей среды. Вывод формулы для истинного угла преломления. Частный случай: поглощающая среда – реальный металл.
- •36. Приближенные граничные условия Леонтовича-Щукина.
- •37. Потери энергии в проводниках. Определение средней мощности джоулевых потерь в проводниках.
- •38. Поверхностное сопротивление проводника.
- •4 2. Режимы работы в однор линии передачи. Понятие о крит частоте. Фаз скор волн в линии передачи. Длина волны в лп.
- •43. Волны типа н в прямоугольном волноводе. Классификация, основные свойства.
- •44. Структура полей волн типа , , . Ст-ра токов провод на стенках волновода для волны . Излуч и неизлуч щели, прорезаемые в стенках волновода.
- •45. Волны типа е в прямоугольном волноводе. Классификация, основные свойства.
- •46. Структура полей волны типа , структура токов проводимости.
- •47. Одноволновый и многоволновый режимы работы волновода. Обеспечение одноволнового режима работы прямоугольного волновода.
- •48. Волны типа н и е в круглом волноводе. Основные свойства. Критическая длина волны. Низшая и высшие типы волн.
- •49. Структура полей волн типа в круглом волноводе.
- •5 0. Обеспечение одноволнового режима работы круглого волновода.
- •51. Волна tem в коакс лин. Фор для полей. Основные св-ва. Стр поля волны tem, стр токов проводи на стенках.
- •53. Обеспечение одноволнового режима работы коаксиальной линии.
- •54. Полосковые линии передачи. Типы линий. Структура полей основной волны. Структура токов проводимости на стенках линии.
- •56. Линии поверхностных (медленных) волн. Простейшие диэлектрические волноводы: конструкция, принцип действия.
- •57.Линии передачи оптического диапазона. Световоды: типы световодов, основные параметры.
- •58. Потери в линиях передачи. Определение потерь в диэлектрическом заполнении и в металлических проводниках.
- •59. Возбуждение волн и колебаний в волноводах и объёмных резонаторах.
4 2. Режимы работы в однор линии передачи. Понятие о крит частоте. Фаз скор волн в линии передачи. Длина волны в лп.
Критическая частота и критическая длина волны. β – действительное и
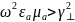
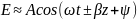 Бегущая волна
Бегущая волна
Стоячая
волна
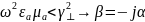
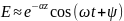
3![]() )
)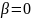 при
при
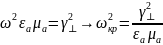 Частота,
на которой
,
наз-ся критической
Частота,
на которой
,
наз-ся критической
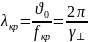
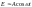
![]()
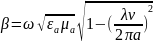
Режимы:
распр
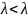 или
или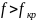 , критический
, критический
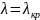 или
или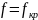 ,
предельный
,
предельный
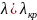 или
или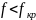 :
: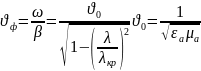 Длина
волны в ЛП:
Длина
волны в ЛП:
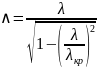
43. Волны типа н в прямоугольном волноводе. Классификация, основные свойства.
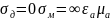 H
– волны:
H
– волны:
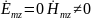
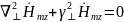
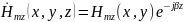
Г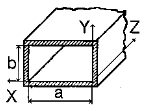 раничные
условия:
раничные
условия:
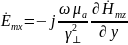 при
при
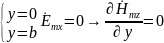
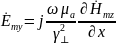 при
при
 Краевая
задача:
Краевая
задача:
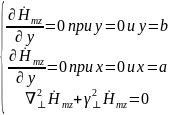 Классификация
магнитных волн в прямоугольном волноводе:
Классификация
магнитных волн в прямоугольном волноводе:
Кл-ция
производ в соответ с индек m
и n.
m-
кол-во полуволн, которые уклад на широ
стенке вол-да. n-
кол-во полуволн, котор уклады вдоль
узкой стенке вол-да.
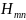 ,
где m=0;1;2;3;…
n=0;1;2;3;…
но волны типа
,
где m=0;1;2;3;…
n=0;1;2;3;…
но волны типа
 нет! Ра-во нулю одного из инд означ, что
поле рассматр волны не зав от соответ
коорд (при m=0
– от коорд х, а при n=0
– от коорд у).
нет! Ра-во нулю одного из инд означ, что
поле рассматр волны не зав от соответ
коорд (при m=0
– от коорд х, а при n=0
– от коорд у).
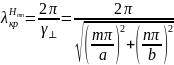
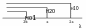
 является
низшей волной
является
низшей волной
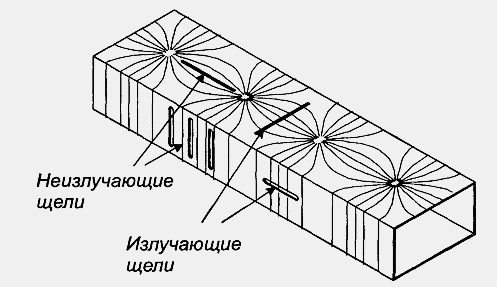
44. Структура полей волн типа , , . Ст-ра токов провод на стенках волновода для волны . Излуч и неизлуч щели, прорезаемые в стенках волновода.
Структура волны типа m=1 n=0
С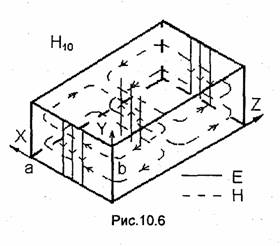 труктура
волн типа
и
труктура
волн типа
и
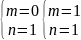
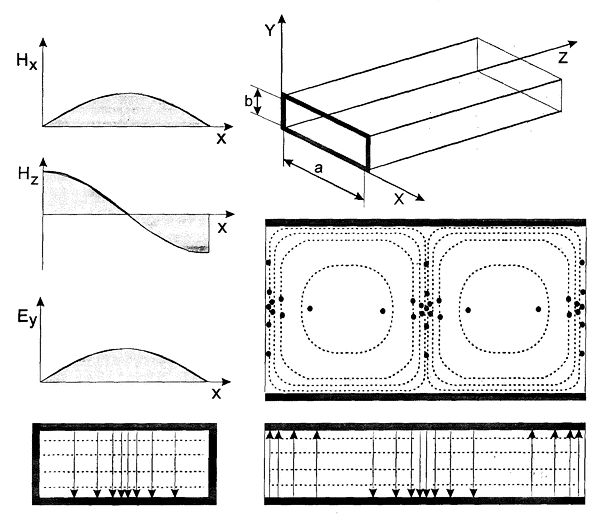
С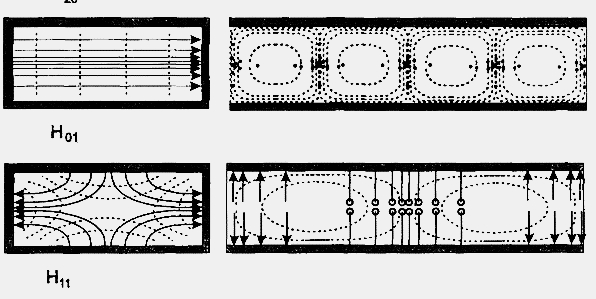 труктура
токов проводимости на стенках волновода
для
.
труктура
токов проводимости на стенках волновода
для
.
45. Волны типа е в прямоугольном волноводе. Классификация, основные свойства.
Уравнение
Гельмгольца для Е волн:
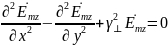 ,
где
,
где
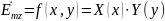 –
функция, у которой одна часть зависит
от x,
другая от у.
–
функция, у которой одна часть зависит
от x,
другая от у.
В
результате преобразования получим
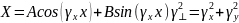
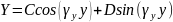
Граничное
условие: Касательные составляющие
эл.поля должны быть равны 0 на всех
стенках.
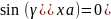 и
и
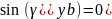
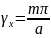 , m=
1, 2,….
, m=
1, 2,….
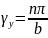 , n=
1, 2, ….
, n=
1, 2, ….
В
таком случае получаем:
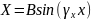
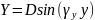 Подставляя получим
Подставляя получим
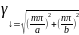 m
– число полуволн на широкой стенке n
– число полуволн на узкой стенке
m
– число полуволн на широкой стенке n
– число полуволн на узкой стенке
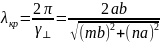
 В
случае E
волн значения m=0
и n=0
не годятся, т.к.
В
случае E
волн значения m=0
и n=0
не годятся, т.к.
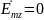 во всех точках внутри волновода, что не
допустимо.
во всех точках внутри волновода, что не
допустимо.
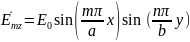
Чтобы
найти
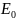 надо знать ещё условие – сколько мощности
распространяется по волноводу.
надо знать ещё условие – сколько мощности
распространяется по волноводу.
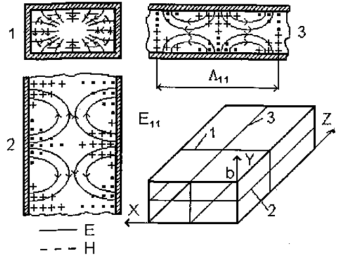
46. Структура полей волны типа , структура токов проводимости.
Структура силовых линий поля будет зависеть от индексов m и n.
Основная
волна
,
так как у неё
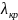 самая большая
самая большая
47. Одноволновый и многоволновый режимы работы волновода. Обеспечение одноволнового режима работы прямоугольного волновода.
Одноволновый
режим – режим, при котором передача
энергии происход одним типом волны, для
этого испол основ волну, имеющую наиб
.
Для этого выбир размеры попереч линий,
чтобы на любой част раб диап длина волны
э/м колеб не превышала крит длины основ
волны
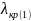 ,
но была больше крит длины волны первого
высшего порядка
,
но была больше крит длины волны первого
высшего порядка
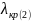 (волна, крит длина которой меньше
основной волны, но больше крит длин всех
остальных зон). Соотв многоволновол
режим работы будет при перед энергии
нескольк типами волн.
(волна, крит длина которой меньше
основной волны, но больше крит длин всех
остальных зон). Соотв многоволновол
режим работы будет при перед энергии
нескольк типами волн.
В
прям волноводе одноволновой режим
работы обеспечивается при размерах:
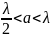 и
и
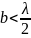
Для
обеспеч одноволнового режима работа
во всем использ диап длин волн
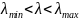 необ, чтобы вып неравенства:
необ, чтобы вып неравенства:
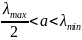 и
и
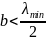
Полосу
частот, в пределах которой сохраняется
одноволновой режим, обычно характеризуют
коэффициентом ширикополосности: