
- •Мощность, излучаемая элементарным электрическим излучателем. Сопротивление излучения. Эквивалентная схема излучателя.
- •Принцип перестановочной двойственности уравнений Максвелла.
- •23. Элементарный магн излучатель. Опред векторов поля, создаваемого излучателем в окруж прост-ве. Анализ структуры поля. Д-ма направленности. Физ модель.
- •24. Элемент Гюйгенса. Направленные свойства.
- •25. Плоские волны в однородной изотропной среде без потерь. Опр векторов поля. Осн св-ва. Фаз скорость. Хар-ое сопрот. Коэф-нт распространения. Длина волны.
- •26. Плоские волны в средах с потерями. Определение векторов поля. Основные свойства. Определения коэффициентов распространения и затухания, понятие дисперсии.
- •27.Математическая запись векторов поля плоской волны, распространяющейся под углом к осям координат.
- •28.Поляризация векторов поля. Виды поляризации.
- •29. Волновые явления на границе раздела двух сред при падении норм- поляриз плоской волны. Законы Снел. Коэфф Френеля.
- •30. Волновые явления на границе раздела двух сред при падении параллельно- поляризованной плоской волны. Законы Снеллиуса. Коэффициенты Френеля.
- •32. Полное внутреннее отражение при падении плоской волны на границу раздела двух сред. Структура поля. Основные свойства. Понятнее о направ волнах типа н и е.
- •33. Падение плоской волны на поверхность идеального металла.
- •34. Принцип действия диэлектрического и металлического волноводов.
- •35. Падение плоской волны на границу поглощающей среды. Вывод формулы для истинного угла преломления. Частный случай: поглощающая среда – реальный металл.
- •36. Приближенные граничные условия Леонтовича-Щукина.
- •37. Потери энергии в проводниках. Определение средней мощности джоулевых потерь в проводниках.
- •38. Поверхностное сопротивление проводника.
- •4 2. Режимы работы в однор линии передачи. Понятие о крит частоте. Фаз скор волн в линии передачи. Длина волны в лп.
- •43. Волны типа н в прямоугольном волноводе. Классификация, основные свойства.
- •44. Структура полей волн типа , , . Ст-ра токов провод на стенках волновода для волны . Излуч и неизлуч щели, прорезаемые в стенках волновода.
- •45. Волны типа е в прямоугольном волноводе. Классификация, основные свойства.
- •46. Структура полей волны типа , структура токов проводимости.
- •47. Одноволновый и многоволновый режимы работы волновода. Обеспечение одноволнового режима работы прямоугольного волновода.
- •48. Волны типа н и е в круглом волноводе. Основные свойства. Критическая длина волны. Низшая и высшие типы волн.
- •49. Структура полей волн типа в круглом волноводе.
- •5 0. Обеспечение одноволнового режима работы круглого волновода.
- •51. Волна tem в коакс лин. Фор для полей. Основные св-ва. Стр поля волны tem, стр токов проводи на стенках.
- •53. Обеспечение одноволнового режима работы коаксиальной линии.
- •54. Полосковые линии передачи. Типы линий. Структура полей основной волны. Структура токов проводимости на стенках линии.
- •56. Линии поверхностных (медленных) волн. Простейшие диэлектрические волноводы: конструкция, принцип действия.
- •57.Линии передачи оптического диапазона. Световоды: типы световодов, основные параметры.
- •58. Потери в линиях передачи. Определение потерь в диэлектрическом заполнении и в металлических проводниках.
- •59. Возбуждение волн и колебаний в волноводах и объёмных резонаторах.
Предмет курса:
Векторы электрического и магнитного полей:
Электрическое
поле
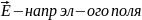 ,
уч-ет действия всех зар.
,
уч-ет действия всех зар.
 ,
хар-ет только вн заряды.
,
хар-ет только вн заряды.
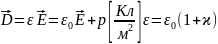 – диэлектрическая
проницаемость Магнитное
поле
– диэлектрическая
проницаемость Магнитное
поле

 ,
,
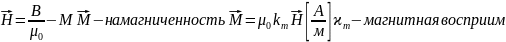
Первое, второе, третье и четвёртое уравнения Максвелла:
Первое: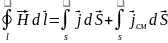 Вихревое
магн. поле соз-тся в тех точках, где есть
токи. Второе:
Вихревое
магн. поле соз-тся в тех точках, где есть
токи. Второе: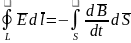 Вихревое эл. поле вызывается перем магн
полем.
Вихревое эл. поле вызывается перем магн
полем.
Третье: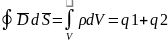 опр
ист-ки элек-го поля.
Четвёртое:
опр
ист-ки элек-го поля.
Четвёртое: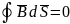 В природе нет потенциального магн. поля.
В природе нет потенциального магн. поля.
Классификация эл-ых явлений: пер по времени, стат, стац и квазистац поля
По
времени:
поле не зависит от времени и отсутствует
перемещение заряженных частиц (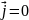 )
)
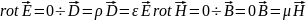
Стат:
незав сущ одного поля без другого. Стац:
эл/м поле, созд пост токами, тогда система
ур. Максвелла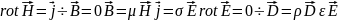
Уравнения Максвелла в комплексной форме:
Первое:
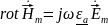 Второе:
Второе:
 Третье:
Третье:
 Четвёртое:
Четвёртое: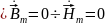
Сторонние источники. Ур-я Максвелла с учётом таких ист.
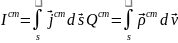 Яв-ся
первоприч поля. 1-ое:
Яв-ся
первоприч поля. 1-ое:
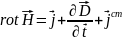 3-e
:
3-e
:
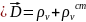 В
случае пер полей
В
случае пер полей
 связ ур-ем непрер
связ ур-ем непрер
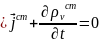
Закон Ома в дифф форме
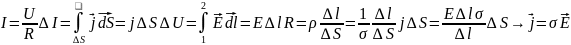
Уравнение непрерывности. Закон сохранения заряда.
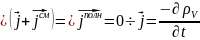 по
т Гаусса
по
т Гаусса
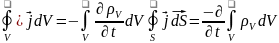
9.Классификация сред по их макроскопическим параметрам:
Нелин:
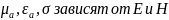 Лин:
Лин:
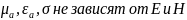 Однор:
Однор: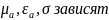 от координат Неодн:
от координат Неодн:
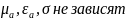 от координат
от координат
Неприменимость ур-й М-ла в диф форме на границе раздела двух сред.
Диффе ур-я М-ла непр на гр раздела сред. Здесь поля не дифф по коорд и операторы div и rotв обычном смысле не сущ. В окр-ти гран поля связ гран ус-ми для их норм и кас проекц.
Вывод граничных условий для нормальных составляющих векторов
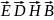 .
.
Применим 3 ур-е М-ла в инт форме к объему цилиндра ∆V, огран поверх ∆S1 и ∆S2 и ∆S
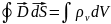 элемент
dS
направлен по внешней нормали к поверхности
элемент
dS
направлен по внешней нормали к поверхности
 ,
поэтому
,
поэтому

У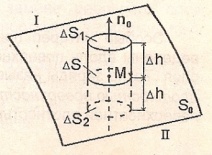 стремляя
∆h
к нулю (при этом
стремляя
∆h
к нулю (при этом
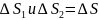 )
)
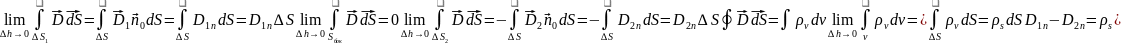 Соотн
показывает, что
Соотн
показывает, что
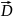 претерп разрыв, равный плотности поверхн
зарядов.
претерп разрыв, равный плотности поверхн
зарядов.
Выражая
в этом соотношении
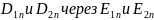 c
помощью равенства
c
помощью равенства
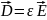 ,
пол-ем
,
пол-ем
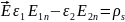
Соотн
пок-ет, что
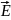 претер разрыв, равный отношению диэл
прон этих сред.
претер разрыв, равный отношению диэл
прон этих сред.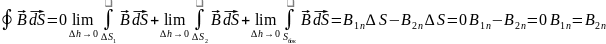
Соотн
показывает, что
 непрер при переходе через границу
раздела двух сред.
непрер при переходе через границу
раздела двух сред.
Из
соотн
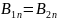 получим
получим
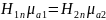 ,
т.к
,
т.к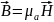
Вывод граничных условий для касательных составляющих векторов .
Грани усл-я могут быть получены из 1 и 2 ур-й М-ла в инт форме. Применим к контуру ABCD первое 1 М-ла
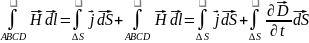
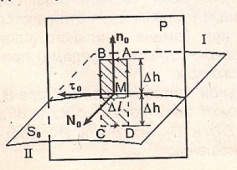 ,
,
 =0,
=0,
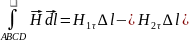
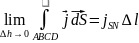 ,
следовательно
,
следовательно
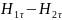 =
=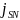 ,
,
если
на гран раздела отсут пов токи, то
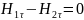
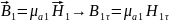

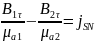
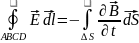 ,
,
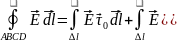 )
)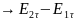
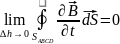
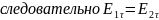
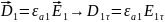
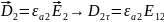
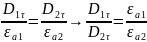
Граничные условия на поверхности идеального проводника. Физический смысл граничных условий.
На
пове раздела любых двух изотр сред
должны вып следующие граничные условия.

Пусть
идеально проводящей является вторая
среда, тогда
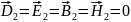 и условия выше принимают вид:
и условия выше принимают вид:
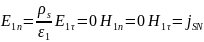
Баланс мгновенных мощностей электромагнитного поля в объёме.
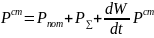 -
мощность стр ист,
-
мощность стр ист,
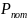 -
мощность дж потерь внутри объёма,
-
мощность дж потерь внутри объёма,
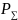 - мощность, прох через пов-ть S,
W
– энергия эл-ого поля.
- мощность, прох через пов-ть S,
W
– энергия эл-ого поля.
Понятие о комплексной мощности. Баланс комплексных мощностей.
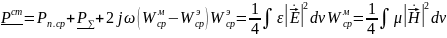
Вектор Пойнтинга: физический смысл, способы вычисления по известным векторам поля.
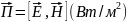 Плотность
пот энергии, прох через площ ΔS
за ед времени. Вектор
напр в сторону перем энергии, а его
величина равна пл потока энергии.
Плотность
пот энергии, прох через площ ΔS
за ед времени. Вектор
напр в сторону перем энергии, а его
величина равна пл потока энергии.
Основные типы задач, решаемых в электродинамике(анализ, синтез).
Вывод волновых уравнений для векторов
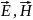 .
.
Для
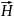 :
:

Для
: , где
, где
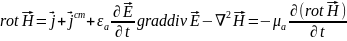 , где
, где
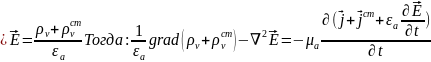

Электродинамические потенциалы. Вывод уравнений для потенциалов. Общее решение таких уравнений. Потенциалы для монохроматического поля.
а)
Связь электромагнитного поля с потенциалом
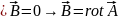 *
*
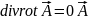 – вект потенциал
– вект потенциал

б)Вывод
вол-го ур-я для потенц

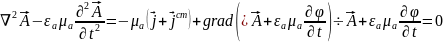 условие
калибровки
условие
калибровки
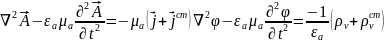
в)постр
об-го ре-я вол-х ур-й для потенц пусть
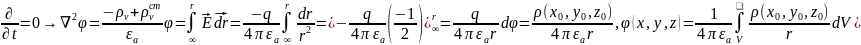
Эле-ый электрический излучатель. Физ модель. Опред век-в поля, созд излем в окружающем пространстве. Анализ структуры поля. Диаграмма направленности.
Излучение – движение энергии от источника. ЭЭВ- короткий по сравн с дл волны провод, обтекаемый эл-м током, амплитуда и фаза которого не изменяются вдоль провода.
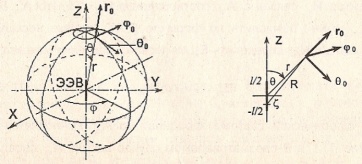
 Опред
векторов поля:
Опред
векторов поля:
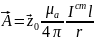
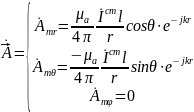
Магнитное
поле:
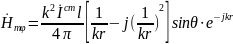 Электрическое
поле:
Электрическое
поле:
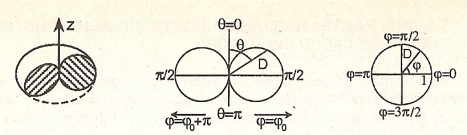
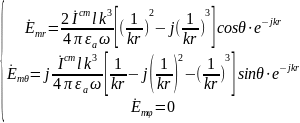 Анализ
структуры поля:
Анализ
структуры поля:
Вектор
напряжённости электрического поля,
создаваемого ЭЭВ, имеет две составляющие
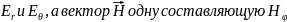 .
.
Зоны:
Ближняя
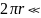 λ
Средняя
λ
Средняя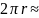 λ
Дальняя
λ
Дальняя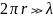 Диа-ма
напр-ти – график зав ампл напряж-ти поля
или ампл её сост от направления в точку
наблюдения при r=const.
Диа-ма
напр-ти – график зав ампл напряж-ти поля
или ампл её сост от направления в точку
наблюдения при r=const.
Мощность, излучаемая элементарным электрическим излучателем. Сопротивление излучения. Эквивалентная схема излучателя.
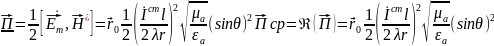 Опред
мощность
Опред
мощность
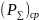
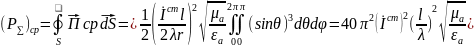
Среда,
занимающая пространство не имеет потерь
– идеальная. Сопротивление излучателя: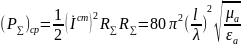
Принцип перестановочной двойственности уравнений Максвелла.
Рассмотрим систему уравнений Максвелла для монохроматического поля.
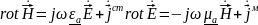 Если
в этих уравнениях формально заменить
Если
в этих уравнениях формально заменить
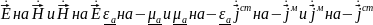 то
первое уравнение превратится во второе
и наоборот
то
первое уравнение превратится во второе
и наоборот
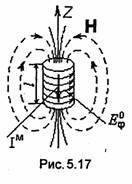
23. Элементарный магн излучатель. Опред векторов поля, создаваемого излучателем в окруж прост-ве. Анализ структуры поля. Д-ма направленности. Физ модель.
Элементарный магнитный излучатель – система, эквивал короткому по сравнению с длиной волны элементу магнитного тока, ампл и фаза к-го один во всех точках этого элемента.
Физическая модель: Рис. 5.19. - Рамка обтекаемая электрическим током.
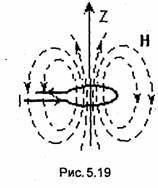
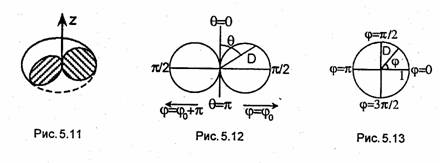 Диаграмма
направленности:
Диаграмма
направленности:
5.11 – пространственная дн 5.12 – дн в меридианальной плоскости, в полярной системе координат 5.13. – нормированная дн, в полярной системе координат
Определение векторов поля, создаваемого излучателем в окружающем пространстве.
В
соответ с принц перестановочной двойст-си
заменим
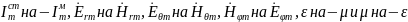 в формулах опред компл амп векторов E
и H
для ЭЭВ:
в формулах опред компл амп векторов E
и H
для ЭЭВ:
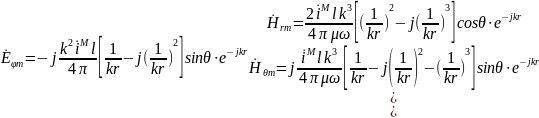 Анализ
структуры поля:
Анализ
структуры поля:
Вектор
напряж магн поля, создаваемого ЭМВ,
имеет две сост
 .
Зоны: Ближняя
λ
Средняя
λ
Дальняя
.
Зоны: Ближняя
λ
Средняя
λ
Дальняя
24. Элемент Гюйгенса. Направленные свойства.
Каждая точка фронта волны, созданной каким-либо перв ист-ом, является втор-им ист-ом сфер волны. Это предполож называют принципом Гюйгенса.
Фронт волны – пов-сть, отд-щая область, в которой в данный момент времени уже имеют место э/м колебания, от области, в которую волна еще не успела распр.
Практически
элемент Гюйгенса можно представить как
элемент фронта распространяющейся
волны.
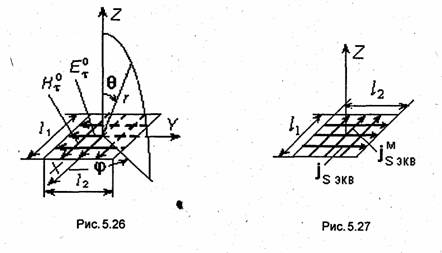 Магн
поле, действ на этом элементе, можно
заменить эк-ным элек-им током, а элек-е
поле – экв-ым магн током. Таким образом,
эл-т Гюйгенса можно рассматр как элем-ый
излуч, обтекаемый электр и магн токами.
Направленные
свойства:Диа-ма
направ эл-та Гюйгенса имеет вид кардиоиды.
Магн
поле, действ на этом элементе, можно
заменить эк-ным элек-им током, а элек-е
поле – экв-ым магн током. Таким образом,
эл-т Гюйгенса можно рассматр как элем-ый
излуч, обтекаемый электр и магн токами.
Направленные
свойства:Диа-ма
направ эл-та Гюйгенса имеет вид кардиоиды.
25. Плоские волны в однородной изотропной среде без потерь. Опр векторов поля. Осн св-ва. Фаз скорость. Хар-ое сопрот. Коэф-нт распространения. Длина волны.
На
больших расстояниях в дальней зоне
любой участок фронта волны можно аппр-ть
плоскостью.
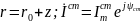
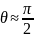 ,
следовательно
,
следовательно
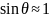 ,
,
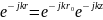
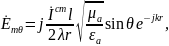 следовательно
следовательно
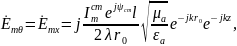
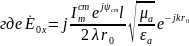
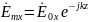
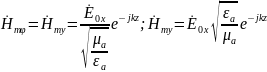
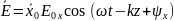
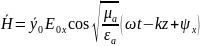
Основные свойства: В среде без потерь сущ только токи пров-ти. Волна яв-ся поперечной. Амплитуды векторов Е и Н не зависят от координат. Вектора Е и Н изменяются синфазно.
Фазовая
скорость:
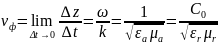 -скорость перемещ фронта волны Хар-ое
сопр-е: т.к. среда без пот
-скорость перемещ фронта волны Хар-ое
сопр-е: т.к. среда без пот
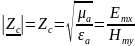 Длина
волны:
Длина
волны:
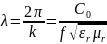
26. Плоские волны в средах с потерями. Определение векторов поля. Основные свойства. Определения коэффициентов распространения и затухания, понятие дисперсии.
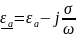 ,
,
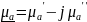
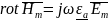 ,
,
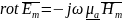
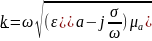 ,
,
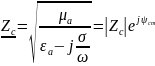
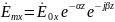
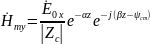
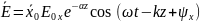
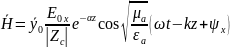 Осн
св-а:
Осн
св-а:
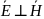 ,
Фаза
поля
,
Фаза
поля
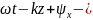 плоск
волна
плоск
волна

Амплитуда поля
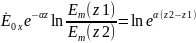 ,
где
,
где
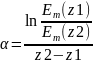 [
[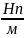 ]
]
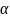 –
показывает насколько Нп уменьшилась
амплитуда.
–
показывает насколько Нп уменьшилась
амплитуда.В среде с потерями вектор Е и Н имеет сдвиг по фазе.
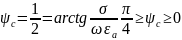
Поскольку Е и Н имеют сдвиг по фазе, то вектор П будет иметь мн часть, т.е. появ реакт мощ. Зав-ть св-в волны (
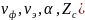 от
f
назыв дисперсией, а соотв-е среды
диспергиру-ми.
от
f
назыв дисперсией, а соотв-е среды
диспергиру-ми.
