10. Понятие игровой ситуации. Игровая ситуация, удовлетворительная для игрока , и доказательство ее критерия. Алгоритм поиска игровых ситуаций, удовлетворительных для игрока .

Ситуация – набор стратегий игроков А и В.

Устойчивая ситуация или ситуация равновесия – ситуация, удовлетворительна для обоих игроков, т.е. когда игроки А и В придерживаются своих максиминной и минимаксной стратегий соответственно, то ни один из них не может увеличить свой выигрыш отступая от своей стратегии: a_ij0≤a_i0j0≤a_i0j , i=1…m, j=1,…,n, или α_i0=a_i0j0=β_jo

Неустойчивая ситуация – ситуация, сложившаяся после первых ходов игры устраивает только одного игрока, например А, тогда игрок В следующим ходом меняет свою стратегию, приводя игру к ситуации, которая не удовлетворяет игрока А.

Теорема Ситуация (Ai0, Bjo) будет удовлетворительна для игрока А Тогда и только тогда, когда его выигрыш совпадет с показателем неэффективности стратегии Bjo игрока В: , то есть будет максимальной в j-ом столбце матрицы игры

Д-во: Пусть ситауция (Ai0, Bjo) удовлетворительна для игрока А. Тогда по определению справедливо нер-во .Из этого неравенства и по определению (1) показателя неэффективности стратегии Bj0 следует, что , то есть нер-во доказано. Тогда применяя (1) при j=j0 получим , то есть доказано

Алгоритм нахождения удовлетворительной ситуации для игрока А:

1. В каждом столбце Bj матрицы А найти max элемент βj

2. Найти строку αi, в которой находится этот элемент.

3. Тогда {Ai; Bj}является удовлетворительной для игрока А.

Причем количество удовлетворительных ситуаций для А больше числа столбцов, но меньше общего числа элементов (n ≤ NAудовл≤ mn)

11. Понятие игровой ситуации. Игровая ситуация, удовлетворительная для игрока , и доказательство ее критерия. Алгоритм поиска игровых ситуаций, удовлетворительных для игрока .

ИГРОВАЯ СИТУАЦИЯ - набор стратегий игроков А и В.

Бывает устойчивой (ситуация, удовлетворительная для обоих игроков) и неустойчивой (ситуация, сложившаяся после первых ходов игры, устраивает только одного игрока).

Теорема. Ситуация (A_i0, B_jo) будет удовлетворительна для игрока В Тогда и только тогда, когда его проигрыш совпадет с показателем эффективности стратегии A_io игрока A: , то есть будет минимален в i-ой строке матрицы игры

Доказательство: Если ситуация (A_i0, B_jo) удовлетворительна для игрока В, то из нер-ва 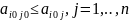и равенства 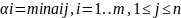при i=i₀ получим и рав-во доказано

Если же это справедливо то по при i=i₀ будем иметь то есть доказано неравенство .

Алгоритм поиска игровых ситуаций, удовлетворительных для игрока В: в каждой строке A_i0 (i₀=1,…,m) матрицы игры находим наименьший элемент α_i0 – показатель эффективности стратегии A_i0 игрока А (которых может быть более одного и не более n), а затем столбец B_i0 , в котором стоит элемент α_{i0 ;} ситуация (A_i0, B_jo) будет удовлетворительной для игрока В.