
Добавил:
Upload
Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Предмет:
Файл:fc2-3.docx
X
- •Задачи теории игр в экономике и в области финансов.
- •Основные понятия и определения теории игр.
- •3. Игра – математическая модель антагонистической ситуации
- •4. Классификация игр по различным признакам
- •5. Матрица выигрышей. Представление игр в нормальной форме
- •6. Максиминный принцип игры
- •7. Минимаксный принцип игры
- •8. Показатели эффективности чистых стратегий. Максиминные и минимаксные стратегии.
- •9. Нижняя и верхняя цены игры в чистых стратегиях. Доказательство теоремы о сравнении нижней и верхней цен игры в чистых стратегиях. Цена игры в чистых стратегиях.
- •10. Понятие игровой ситуации. Игровая ситуация, удовлетворительная для игрока , и доказательство ее критерия. Алгоритм поиска игровых ситуаций, удовлетворительных для игрока .
- •11. Понятие игровой ситуации. Игровая ситуация, удовлетворительная для игрока , и доказательство ее критерия. Алгоритм поиска игровых ситуаций, удовлетворительных для игрока .
- •12. Ситуация равновесия. Седловая точка игры. Седловая точка матрицы выигрышей.
- •13. Доказательство теоремы о свойстве равнозначности седловых точек.
- •14. Доказательство теоремы о свойстве взаимозаменяемости седловых точек.
- •15. Стратегии, оптимальные во множестве чистых стратегий. Полное (общее) и частное решение игры в чистых стратегиях.
- •16. Соотношения между множествами оптимальных, максиминных и минимаксных стратегий. Доказательство.
- •17. Понятие смешанной стратегии.
- •18. Геометрическая интерпретация множества смешанных стратегий.
- •19. Выигрыш-функция в смешанных стратегиях и различные формулы ее представления.
- •20. Показатель эффективности смешанной стратегии игрока относительно множества смешанных стратегий игрока и доказательство теоремы о его существовании.
- •21. Показатель эффективности смешанной стратегии игрока относительно множества смешанных стратегий игрока и доказательство теоремы о его существовании.
- •24. Нижняя и верхняя цены игры в смешанных стратегиях.
- •25. Доказательство теоремы о существовании в любой конечной матричной игре нижней и верхней цен игры в смешанных стратегиях.
- •26. Доказательство теоремы о сравнении нижних и верхних цен игры в чистых и смешанных стратегиях.
- •27. Понятие стратегии, оптимальной во множестве смешанных стратегий. Основная теорема матричных игр Дж. Фон Неймана.
- •32. Доказательство теоремы о геометрической интерпретации множества стратегий игрока а, оптимальных во множестве смешанных стратегий.
- •33.Доказательство теоремы о геометрической интерпретации множества стратегий игрока , оптимальных во множестве смешанных стратегий.
- •37. Определение активных и пассивных чистых стратегий и доказательство теоремы об активных стратегий.
- •38. Определение смесей активных стратегий и доказательство теоремы о смесях активных стратегий.
- •39. Принцип доминирования. Теорема о доминирующих стратегиях и следствия из нее.
- •40. Доказательство критерия седловой точки матрицы игры размерности 2х2 на основании принципа доминирования.
- •41. Доказательство критерия седловой точки матрицы игры размерностим 2х2 в терминах пассивных стратегий.
- •42. Доказательство теоремы о признаке (достаточном условии) существования седловой точки матрицы игры размерности 2х2.
- •43. Вывод формул для нахождения оптимальных смешанных стратегий игрока а и цены игры размерности 2х2 без седловой точки.
- •44. Вывод формул для нахождения оптимальных смешанных стратегий игрока в и цены игры размерности 2х2 без седловой точки.
- •45. Аналитическое решение игры без седловой точки, задаваемой симметрической и двоякосимметрической матрицей второго порядка.
- •46. Геометрический метод нахождения оптимальных смешанных стратегий игрока и цены игры в смешанных стратегиях в игре размерности без седловой точки.
- •47. Геометрический метод нахождения оптимальных смешанных стратегий игрока и цены игры в смешанных стратегиях в игре размерности без седловой точки.
- •48. Геометрический метод нахождения оптимальных смешанных стратегий игрока и цены игры в смешанных стратегиях в игре размерности .
- •49. Доказательство формул для нахождения цены игры в смешанных стратегиях и стратегий игрока , оптимальных во множестве смешанных стратегий, в игре размерности .
- •50. Теорема о необходимом и достаточном условии оптимальности смешанной стратегии игрока в игре размерности .
49. Доказательство формул для нахождения цены игры в смешанных стратегиях и стратегий игрока , оптимальных во множестве смешанных стратегий, в игре размерности .
![]()
![]()
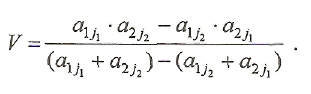
Доказательство
Уравнения
отрезков
![]() и
и
![]() имеют следующий вид:
имеют следующий вид:
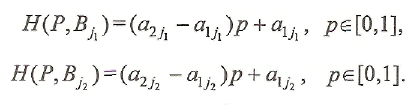
Так как эти отрезки пересекаются в точке N, то абсцисса р0 этой точки является решением уравнения
![]()
откуда получаем формулу
.
Поскольку цена игры Vпредставляет собой ординату точки N, то для вычисления Vдостаточно в правую часть одного из равенств
подставить вместо р абсциссу р0, выраженную формулой
.
Подставляя р = р0в правую часть равенства , получим
![]()
50. Теорема о необходимом и достаточном условии оптимальности смешанной стратегии игрока в игре размерности .
Пусть
через максимальную точку N нижней
огибающей отрезков ![]() ,
j=
1,..., п,
порождаемых чистыми стратегиями
Bj,
j
=1,..., n,
игрока В, проходят два каких-либо отрезка
,
j=
1,..., п,
порождаемых чистыми стратегиями
Bj,
j
=1,..., n,
игрока В, проходят два каких-либо отрезка
![]() u
u
![]()
Для
того чтобы смешанная стратегия Q°
![]() игрока
B, где
игрока
B, где
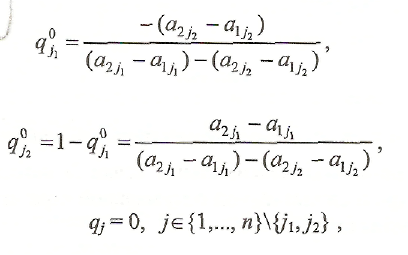
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
