47. Геометрический метод нахождения оптимальных смешанных стратегий игрока и цены игры в смешанных стратегиях в игре размерности без седловой точки.

Берем горизонтальный отрезок [0, 1], на котором для определенности положено

а₂₂< а₁₁< а₂₁< а₁₂

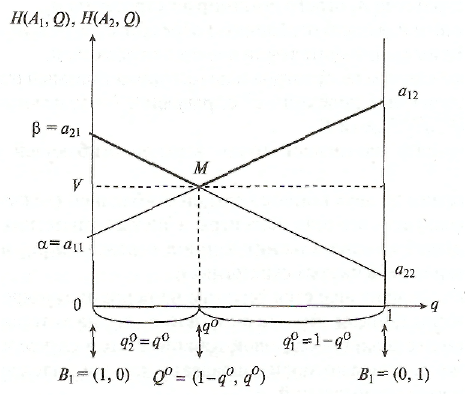
2. В концах отрезка [0, 1] проводим к нему два перпендикуляра: левый, соответствующий стратегии В₁и правый, соответствующий стратегии В₂,

3. На левом перпендикуляре от точки 0 его пересечения с отрезком [0, 1] откладываем (как на вертикальной числовой оси) элементы а₁₁и а₂₁первого столбца матрицы А.

4. На правом перпендикуляре от точки 1 его пересечения с отрез­ком [0, 1] откладываем (как на вертикальной числовой оси) элементы а₁₂и а₂₂второго столбца матрицы А.

5. Соединяем точки, изображающие элементы с одинаковыми первыми индексами, т.е. элементы, стоящие в одной и той же строке матрицы А: а₁₁с а₁₂и а₂₁ са₂₂. В результате получаем отрезки а₁₁а₁₂и а₂₁а₂₂

6. Если отрезки а₁₁а₁₂и а₂₁а₂₂ невозрастающие: а₁₁а₁₂и а₂₁а₂₂ то стратегия В₂доминирует стратегию В₁.

Если отрезки а₁₁а₁₂и а₂₁а₂₂ убывающие: а₁₁а₁₂и а₂₁а₂₂ , то страте­гия В₂строго доминирует стратегию В₁.

7. Если отрезок а₁₁а₁₂лежит не ниже отрезка а₂₁а₂₂ то стратегия А₁ доминирует стратегию А₂.

Если отрезок а₁₁а₁₂лежит выше отрезка а₂₁а₂₂ и не пересекается с ним, то стратегия А₁строго доминирует стратегию А₂.

8. Находим верхнюю огибающую отрезков а₁₁а₁₂и а₂₁а₂₂.

9. Находим наинизщие точки верхней огибающей.

10. Проектируем их ортогонально на горизонтальный отрезок [0, 1].

11. Полученные проекции q° определяют оптимальные стратегии Q°= (1-q⁰,q°) игрока В.

12. Ордината наинизшей точки верхней огибающей равна цене игры V.

13. Нижний из двух концов верхней огибающей (лежащих на пер­пендикулярах) есть верхняя цена игры в чистых стратегиях .

14. Верхний из двух нижних концов отрезков а₁₁а₁₂и а₂₁а₂₂ есть нижняя цена игры в чистых стратегиях .

Если элемент является верхним на перпендикуляре, где он ле­жит, и нижним концом отрезка а₁₁а₁₂или а₂₁а₂₂, на котором он лежит, то этот элемент является седловой точкой. В этом случае чистая стра­тегия игрока А, номер которой совпадает с первым индексом седловой точки, является оптимальной.

48. Геометрический метод нахождения оптимальных смешанных стратегий игрока и цены игры в смешанных стратегиях в игре размерности .

Берем горизонтальный отрезок [0, 1].

Через концы отрезка [0,1] проводим к нему два перпендикуляра: левый и правый.

На левом перпендикуляре от точки 0 его пересечения с отрезком [0, 1] откладываем (как на вертикальной числовой оси) все элементы первой строки матрицы А.

На правом перпендикуляре от точки 1 его пересечения с отрез­ком [0, 1] откладываем (как на вертикальной числовой оси) все эле­менты второй строки матрицы А.

Каждую пару точек, изображающих элементы а_1j и a_2j, j=1,2,..., п, стоящие j-м столбце матрицы A, соединяем отрезком а_1ja_2j. Таким образом, будут построены п отрезков, представляющих собой графики и линейных функций

где Р= (1 — р, р) — смешанная стратегия игрока А.

Если все отрезки а_1ja_2j, j=1,2,..., п, неубывающие (имеют неот­рицательный наклон), то стратегия А₂доминирует стратегию А₁.

Если все отрезки а_1ja_2j, j=1,2,..., п, возрастающие (имеют поло­жительный наклон), то стратегия А₂строго доминирует стратегию А₁.

Если все отрезки а_1ja_2j, j=1,2,..., п, невозрастающие (имеют не­положительный наклон), то страте­гия А₁доминирует стратегию А₂.

Если все отрезки а_1ja_2j, j=1,2,..., п, убывающие (имеют отрица­тельный наклон), то стратегия А₁строго доминирует стратегию А₂.

Находим (выделяем) нижнюю огибающую семейства отрезков , которая в общем случае будет представлять собой выпуклую вверх ломаную, а, в частности, может быть и отрезком.

На нижней огибающей находим наивысшую точку (точки).

Абсцисса р° этой точки является вероятностью выбора игро­ком А чистой стратегии А₂в оптимальной смешанной стратегии Р° = (1 – р⁰, р⁰)

Ордината наивысшей точки нижней огибающей является це­ной игры V.

Верхний из двух концов нижней огибающей (лежащих на пер­пендикулярах) есть нижняя цена игры в чистых стратегиях .

Нижний из верхних концов отрезков а_1ja_2j, j=1,2,..., п, есть верхняя цена игры в чистых стратегиях .

Элемент матрицы А, изображающая точка которого является нижней на перпендикуляре, где она лежит, и верхним концом отрезка, на котором она лежит, будет седловой точкой игры.

В этом случае чистая стратегия игрока В, номер которой совпадает со вторым индексом седловой точки, является оптимальной.

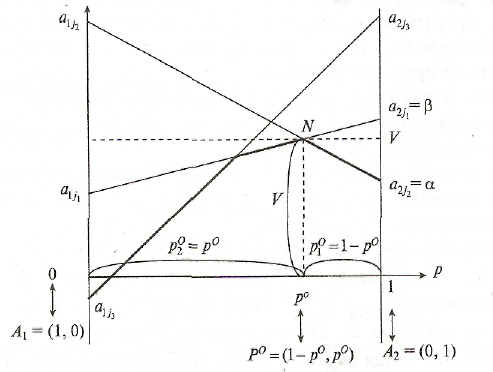
На рисунке из п отрезков а_1ja_2j, j=1,2,..., п, указаны три, которые принимают участие в конструировании нижней огибающей, выделенной жирной линией; Н — наивысшая точка этой огибающей; р° — абсцисса точки N, следовательно, Р° = (1 — р°, р°) — оптимальная смешанная стратегия игрока А, цена игры К равна ординате точки N; нижняя цена игры в чистых стратегиях  = a_2j2;верхняя цена игры в чистых стратегиях  = a_2j1; на рисунке видно, что <V<.