37. Определение активных и пассивных чистых стратегий и доказательство теоремы об активных стратегий.

Пусть V-цена игры, Р° = {р₁^O_,…,р_m^O) и Q° =(q₁^O,...,q_n^O) - оптимальные стратегии соответственно игроков А и В. Тогда справедливы следующие утверждения.

1. Для любой активной стратегии A_k (k∈{1,...,m}) игрока А выполняется равенство

H(A_k,Q°)=V (1)

2. Для любой активной стратегии B_l (l∈ {1,…,n}) игрока В выполняется равенство

Н(Р°, В_l) = V (2)

Доказательство. Докажем утверждение 1 теоремы. Допустим противное этому утверждению, т. е. предположим, что найдется активная стратегия А_k игрока А такая, что

H(A_k,Q°)≠V (3)

Так как Q^O- оптимальная стратегия игрока В, a V- цена игры, то по необходимой части теоремы (вопрос 30)

H(A_i, Q^O) ≤ V, i=1,…,m (4)

В частности, неравенство (4) будет справедливым и для i=k, т. е.

H(A_k, Q^O) ≤ V

Отсюда и из предположения (3) следует строгое неравенство

H(A_k, Q^O) <V (5)

Так как А_k активная стратегия, то по определению p_k^O> 0 и тогда из (5) получаем

p_k^OH(A_k,Q^O)<p_k^OV (6)

Для остальных номеров i, отличных от k, из (4), учитывая, что р_k^O> 0, имеем

p_i^OН(A_i, Q^O) < р_i^OV, i∈ {1,...,m}\{k} (7)

Суммируя неравенства (6) и (7) и помня, что , получим

а, по формуле H(P,Q)=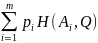 (9)

и потому (8) можно переписать в виде неравенства

H(P°,Q°)<V.

Но так как V - цена игры, а Р° и Q^O - оптимальные стратегии, то по их определению должно выполняться равенство

H(P°,Q°) = V

Полученное противоречие доказывает утверждение 1 теоремы. Утверждение 2 доказывается аналогично. В предположении противного утверждению 2 найдется активная стратегия В_l игрока В, для которой

(9)

Поскольку Р^О – оптимальная стратегия игрока А, aV – цена игры, то по критерию оптимальности смешанной стратегии

Из этого неравенства при j=1 и предположения (9) следует, что

Из которого в силу того, что q₁⁰>0, получаем

Из (10)

Просуммировав неравенства (11) и (12) и применив формулу

получим неравенство

Которое противоречит равенству H(P°,Q°) = V, определяющему оптимальные стратегии P⁰ и Q⁰. Утверждение 2 доказано.

38. Определение смесей активных стратегий и доказательство теоремы о смесях активных стратегий.

Пусть V- цена игры, Р° = (р₁^O ,…,р_m^O) и Q° =(q₁^O,...,q_n^O) - оптимальные смешанные стратегии соответственно игроков А и В. Тогда справедливы утверждения.

1. Для любой смеси активных стратегий Р = (р₁,…,р_m) игрока А справедливо равенство

H(P,Q°) = V (1)

2. Для любой смеси активных стратегий Q =(q₁,...,q_n) В справедливо равенство

H(Р°,Q) = V (2)

Доказательство. Докажем утверждение 1. По формуле (9 вопрос 37)

Так как Р = (р₁,…,р_m) - смесь активных стратегий, то p_i = 0 для i не ∈ I и потому вторая сумма в правой части равенства (3) равна нулю. В первой сумме в правой части (3) суммирование ведется по индексу i∈ I и значит ( ) р_i> 0, а следовательно, A_i, i∈ I - активные стратегии игрока А. Тогда, на основании утверждения 1 (вопроса 37) об активных стратегиях H(A_i,Q°) = V, i∈ I. Поэтому из (3) получаем равенство (1):

Аналогичным образом можно доказать и утверждение 2. А именно, по формуле с использованием и утверждения 2 (вопроса 37) об активных стратегиях имеем