24. Нижняя и верхняя цены игры в смешанных стратегиях.

Нижней ценой, или максимином, матричной игры в смешанных стратегиях называется величина

Верхней ценой, или минимаксом, матричной игры в смешанных стратегиях называется величина

Для любой конечной матрицы игры существуют нижняя и верхняя цена игры в смешанных стратегиях.

Смешанная стратегия P⁰∈ SA, максимизирующая показатель эффективности α(Р), называется максиминной смешанной стратегией игрока А. Таким образом V= maxР∈SA α(P) = α(P⁰). Множество всех максиминных смешанных стратегий игрока А обозначим через (SА)^maxmin.

Смешанная стратегия Q⁰∈SB, минимизирующая показатель неэффективности β (Q), называется минимаксом смешанной стратегии игрока В. Таким образом, v̅ = minQ ∈ SB β (Q) = β (Q⁰). Множество всех минимаксных смешанных стратегий игрока В обозначается (SВ) ^{min max} .

Нижняя цена игры α и верхняя цена игры β в чистых стратегиях, нижняя цена игры V и верхняя цена игры v̅ в смешанных стратегиях удовлетворяют следующем неравенствам

α ≤ V ≤ v̅≤ β

25. Доказательство теоремы о существовании в любой конечной матричной игре нижней и верхней цен игры в смешанных стратегиях.

Нижней ценой (или максимином) матричной игры в смешанных стратегиях называется величина

Верхней ценой (или минимаксом) матричной игры в смешанных стратегиях называется величина

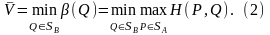
Т.к. ф-я α(Р) непрерывна на компакте S_A, то она достигает на этом множестве своего максимума, т.е. сущ нижняя цена игры в смеш стр-х: Аналогично:

Смеш стратегия P^О S_A, максимизирующая показатель эффективности α(Р), назовем максиминной смешанной стратегией игрока А. Т.о., нижняя цена игры есть показатель эффективности максиминной смеш стр-и P^О: (В частном случае P^О = является максиминной чистой стратегией игрока A. )

Аналогично, смешанную стратегия Q^О S_B, минимизирующая показатель неэффективности β(Q), назовем минимаксной смешанной стратегией игрока В. Показатель неэффективности минимаксной смешанной стратегии Q^О равен верхней цене игры : (Если Q^О = то является минимаксной чистой стратегией.)

26. Доказательство теоремы о сравнении нижних и верхних цен игры в чистых и смешанных стратегиях.

Теорема. Нижняя цена игры α и верхняя цена игры β в чистых стратегиях, нижняя цена игры и верхняя цена игры в смешанных стратегиях удовлетворяют следующим неравенствам:

Доказательство. Начнем д-во с неравенства . По определению нижней цены игры в смешанных стратегиях 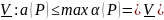. Здесь правая часть не зависит от Р и потому это неравенство остается верным и для Р=Аi, i=1…m. Так как полученное равенство будет справедливым в частности для того номера i, который максмизирует показатель эффективности , Доказано.

Докажем второе неравенство . Для любых Р принадлежащих Sa и Q принадлежащих Sb имеем:

Так как утверждение справедливо для любых Р принадлежащих Sa и Q принадлежащих Sb, то

Докажем третью часть . . 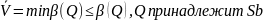Это также верн и для чистых стратегий Q=Bj, j=1,…,n игрока В 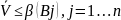. Следовательно, ч.т.д.