Вопрос 4

Точная верхняя граница (верхняя грань) и точная нижняя граница (нижняя грань) — обобщение понятий максимума и минимума множества соответственно.

Используемые определения

Мажоранта или верхняя грань (граница) множества   — число  , такое что  . Миноранта или нижняя грань (граница) множества   — число  , такое что 

[Править]Определения

Точной (наименьшей) верхней гранью (границей), или супре́мумом (лат. supremum — самый высокий) подмножества   упорядоченного множества (или класса)  , называется наименьший элемент  , который равен или больше всех элементов множества  . Другими словами, супремум — это наименьшая из всех верхних граней. Обозначается  .

Более формально:

 — множество верхних граней  , то есть элементов  , равных или больших всех элементов 

Точной (наибольшей) нижней гранью (границей), или и́нфимумом (лат. infimum — самый низкий) подмножества   упорядоченного множества (или класса)  , называется наибольший элемент  , который равен или меньше всех элементов множества  . Другими словами, инфимум — это наибольшая из всех нижних граней. Обозначается  .

[Править]Замечание

Эти определения ничего не говорят о том, принадлежит ли   и   множеству   или нет.

В случае  , говорят, что   является максимумом  , то есть  .

В случае  , говорят, что   является минимумом  , то есть  .

Вопрос 5 Десятичная запись вещественного числа

Определение. Числа рациональные и иррациональные называют вещественными или действительными числами.

Обозначение.   (real) — множество вещественных чисел.

Пусть  .

Найдем наибольшее целое число  , не превосходящее  :  . Предположим, что у нас получилось  ,   (см. рис. 7):

Рис. 7

Разобьем отрезок   на 10 равных частей и выберем ту из этих частей, которая содержит   (рис. 8):

Рис. 8

где   — десятичная цифра.

Разобьем отрезок на 10 равных частей и выберем ту из этих частей, которая содержит   (рис. 9):

Рис. 9

и т.д.

Если  , то получим

Определение. Бесконечная десятичная дробь  , где   получаются указанным способом, называется десятичной записьючисла  .

Вопрос 6

Арифметические операции над вещественными числами определяются как непрерывное продолжение соответствующих операций над рациональными числами. Например, суммой вещественных чисел   и   называется вещественное число  , удовлетворяющее следующему условию:

Вопрос 7

I. Существование  , 

Пусть  . Корень  -й степени из   — такое вещественное число  , что  . Рассмотрим случай, когда   и будем искать  , удовлетворяющее этому соотношению, т.е. арифметическое значение корня.

Возьмем возрастающую последовательность рациональных чисел  .

Докажем, что последовательность  .

Последовательность   возрастает. Действительно, предположим противное:  . Тогда, по свойствам неравенств, будем иметь  , что противоречит возрастанию  . Аналогично доказывается ее ограниченность. Возьмем рациональное число  . Тогда, очевидно,  . Таким образом, последовательность   имеет предел. По теореме о пределе произведения

т.е.  .

Вопрос 8 Вещественный логарифм

Логарифм вещественного числа   по определению есть решение уравнения   Случай   интереса не представляет, поскольку тогда при   это уравнение не имеет решения, а при   любое число является решением; в обоих случаях логарифм не определён. Аналогично заключаем, что логарифм не существует при нулевом или отрицательном  ; кроме того, значение показательной функции   всегда положительно, поэтому следует исключить также случай отрицательного  . Окончательно получаем^[5]:

Вещественный логарифм   имеет смысл при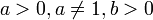

Как известно, показательная функция   (при выполнении указанных условий для  ) существует, монотонна и каждое значение принимает только один раз, причём диапазон её значений содержит все положительные вещественные числа^[6]. Отсюда следует, что значение вещественного логарифма положительного числа всегда существует и определено однозначно.

Наиболее широкое применение нашли следующие виды логарифмов.

• Натуральные: 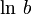 , основание: число Эйлера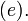 

• Десятичные: 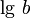 , основание: число