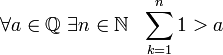Вопрос 1 Множество рациональных чисел
Множество
рациональных чисел обозначается 
и
может быть записано в таком виде:
При
этом оказывается, что разные записи
могут представлять одну и ту же дробь,
например, 
и 
,
(все дроби, которые можно получить друг
из друга умножением или делением на
одно и то же натуральное число, представляют
одно и то же рациональное число). Поскольку
делением числителя и знаменателя дроби
на их наибольший
общий делитель можно
получить единственное несократимое
представление рационального числа, то
можно говорить об их множестве как о
множестве несократимых дробей
со взаимно
простыми целым
числителем и натуральным знаменателем:
Здесь 
—
наибольший общий делитель чисел 
и 
.
Множество
рациональных чисел является естественным
обобщением множества целых
чисел.
Легко видеть, что если у рационального
числа 
знаменатель 
,
то 
является
целым числом. Множество рациональных
чисел располагается на числовой оси
всюду плотно: между любыми двумя
различными рациональными числами
расположено хотя бы одно рациональное
число (а значит, и бесконечное множество
рациональных чисел). Тем не менее,
оказывается, что множество рациональных
чисел имеет счётную мощность (то
есть все его элементы можно перенумеровать).
Заметим, кстати, что ещё древние греки
убедились в существовании чисел, не
представимых в виде дроби (например,
они доказали, что не существует
рационального числа, квадрат которого
равен 2).
Основные свойства
Множество рациональных чисел удовлетворяют шестнадцати основным свойствам, которые легко могут быть получены из свойств целых чисел.[1]
Упорядоченность. Для любых рациональных чисел
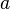и 
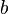существует
правило, позволяющее однозначно
идентифицировать между ними одно и
только одно из трёх отношений:
«
»,
«
»
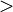или «
».
Это правило называется правилом
упорядочения и
формулируется следующим образом: два
положительных числа 
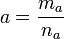и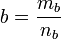 
связаны
тем же отношением, что и два целых
числа 
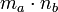и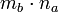 
;
два неположительных числа
и
связаны
тем же отношением, что и два неотрицательных
числа 
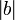и 
;
если же вдруг
неотрицательно,
а
—
отрицательно, то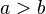 
.
Операция сложения. Для любых рациональных чисел и существует так называемое правило суммирования, которое ставит им в соответствие некоторое рациональное число
.
При этом само число
называется суммой чисел
и
и
обозначается 
,
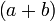а процесс отыскания такого числа
называется суммированием.
Правило суммирования имеет следующий
вид: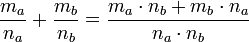 
.
Операция умножения. Для любых рациональных чисел и существует так называемое правило умножения, которое ставит им в соответствие некоторое рациональное число . При этом само число называется произведением чисел и и обозначается
,
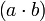а процесс отыскания такого числа также
называется умножением.
Правило умножения имеет следующий
вид: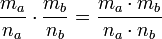 
.
Транзитивность отношения порядка. Для любой тройки рациональных чисел , и если меньше и меньше , то меньше , а если равно и равно , то равно .
Коммутативность сложения. От перемены мест рациональных слагаемых сумма не меняется.
Ассоциативность сложения. Порядок сложения трёх рациональных чисел не влияет на результат.
Наличие нуля. Существует рациональное число 0, которое сохраняет любое другое рациональное число при суммировании.
Наличие противоположных чисел. Любое рациональное число имеет противоположное рациональное число, при суммировании с которым даёт 0.
Коммутативность умножения. От перемены мест рациональных множителей произведение не меняется.
Ассоциативность умножения. Порядок перемножения трёх рациональных чисел не влияет на результат.
Наличие единицы. Существует рациональное число 1, которое сохраняет любое другое рациональное число при умножении.
Наличие обратных чисел. Любое ненулевое рациональное число имеет обратное рациональное число, умножение на которое даёт 1.
Дистрибутивность умножения относительно сложения. Операция умножения согласована с операцией сложения посредством распределительного закона:
Связь отношения порядка с операцией сложения. К левой и правой частям рационального неравенства можно прибавлять одно и то же рациональное число.
Связь отношения порядка с операцией умножения. Левую и правую части рационального неравенства можно умножать на одно и то же положительное рациональное число.
Аксиома Архимеда. Каково бы ни было рациональное число , можно взять столько единиц, что их сумма превзойдёт .
