Вопрос 3. Закон Ампера. Взаимодействие параллельных токов

Как нам уже известно, магнитное поле оказывает на рамку с током ориентирующее действие. Значит, вращающий момент, который испытывает рамка, является результатом действия сил на отдельные ее элементы. Сравнивая и обобщая результаты исследования действия магнитного поля на различные проводники с током, Ампер открыл, что сила dF, с которой магнитное поле действует на элемент проводника dl с током, который находится в магнитном поле, равна (1) где dl - вектор, по модулю равный dl и совпадающий по направлению с током, В - вектор магнитной индукции. Направление вектора dF может быть определено, используя (1), по правилу векторного произведения, откуда следует правило левой руки: если ладонь левой руки расположить так, чтобы в нее входил вектор В, а четыре вытянутых пальца расположить по направлению тока в проводнике, то отогнутый большой палец покажет направление силы, которая действуюет на ток. Модуль силы Ампера (см. (1)) равен (2) где α — угол между векторами dl и В. Закон Ампера используется при нахождении силы взаимодействия двух токов. Рассмотрим два бесконечных прямолинейных параллельных тока I₁ и I₂; (направления токов даны на рис. 1), расстояние между которыми R. Каждый из проводников создает вокруг себя магнитное поле, которое действует по закону Ампера на соседний проводник с током. Найдем, с какой силой действует магнитное поле тока I₁ на элемент dl второго проводника с током I₂. Магнитное поле тока I₁ есть линии магнитной индукции, представляющие собой концентрические окружности. Направление вектора B₁ задается правилом правого винта, его модуль по формуле (5) есть Направление силы dF₁, с которой поле B₁ действует на участок dl второго тока, находится по правилу левой руки и указано на рисунке. Модуль силы, используя (2), с учетом того, что угол α между элементами тока I₂ и вектором B₁ прямой, будет равен подставляя значение для В₁, найдем (3) Аналогично рассуждая, можно показать, что сила dF₂ с которой магнитное поле тока I₂ действует на элемент dl первого проводника с током I₁, направлена в противоположную сторону и по модулю равна (4) Сопоставление выражений (3) и (4) дает, что т. е. два параллельных тока одинакового направления притягиваются друг к другу с силой, равной (5) Если токи имеют противоположные направления, то, используя правило левой руки, определим, что между ними действует сила отталкивания, определяемая выражением (5).

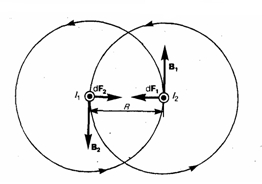
Рис.1

Вопрос 4

Любой проводник с током создает в окружающем пространстве магнитное поле. При этом электрический же ток является упорядоченным движением электрических зарядов. Значит можно считать, что любой движущийся в вакууме или среде заряд порождает вокруг себя магнитное поле. В результате установлен закон, который определяет поле В точечного заряда Q, движущегося с постоянной нерелятивистской скоростью v. Этот закон задается формулой (1) где r — радиус-вектор, который проведен от заряда Q к точке наблюдения М (рис. 1). Согласно (1), вектор В направлен перпендикулярно плоскости, в которой находятся векторы v и r : его направление совпадает с направлением поступательного движения правого винта при его вращении от v к r.

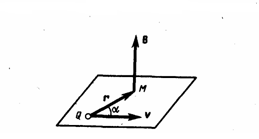
Рис.1

Модуль вектора магнитной индукции (1) находится по формуле (2) где α—угол между векторами v и r. Сопоставляя закон Био-Савара-Лапласа и (1), мы видим, что движущийся заряд по своим магнитным свойствам эквивалентен элементу тока: Приведенные законы (1) и (2) выполняются лишь при малых скоростях (v<<с) движущихся зарядов, когда электрическое поле движущегося с постоянной скорость заряда можно считать электростатическим, т. е. создаваемым неподвижным зарядом, который находится в той точке, где в данный момент времени находится движущийся заряд. Формула (1) задает магнитную индукцию положительного заряда, движущегося со скоростью v. При движении отрицательнго заряда Q заменяется на -Q. Скорость v - относительная скорость, т. е. скорость относительно системы отсчета наблюдателя. Вектор В в данной системе отсчета зависит как от времени, так и от расположения наблюдателя. Поэтому следует отметить относительный характер магнитного поля движущегося заряда. сила Лоренса

Сила действующая на движущийся заряд со стороны магнитного поля- назыв. силой Лоренца F=q[BV]. Направление этой силы опред. правилом левой руки: если ладонь левой руки расположить так чтобы в нее входил вектор В,а 4 вытянутых пальца направить вдоль вектора ,то отогнутый большой палец покажет направление силы, действующий на положительный заряд. Модуль силы Лоренца: F_Л= qVB*sin α. Магнитное поле не действует на покоящийся электрический заряд. В этом существенное отличие магнитного поля от электрического. Магнитное поле действует только на движущиеся в нем заряды. По действию силы Лоренца можно найти модуль и направление вектора В,для определения вектора магнитной индукции. Сила Лоренса всегда перпендекулярна скорости движения заряженной частици,поэтому она изменяет только направление движения не изменяя модуль скорости т.е сила лоренса не совершает работу. Е_К частицы в магнитном поле не изменяется. Если на заряд помимо магнитного поля действует еще электрическое поле то результ-я сила = векторной сумме F =qE+q[BV].