
- •33.Непрерывность функции в точке
- •34.Непрерывность функций на отрезке
- •Свойства функций, непрерывных на отрезке
- •35. Определение производной функции.
- •36. Касательная и нормаль к графику функции. Правила дифференцирования.
- •Правила дифференцирования.
- •37. Производные основных и элементарных функций.
- •38.Производная сложной функции, обратной и неявной функции, сложной показательной функции.
- •39. Дифференциал функции. Геометрический смысл дифференциала. Правила дифференцирования. Дифференциал высших порядков.
- •Дифференциал высшего порядка функции одной переменной
- •40.Производные высших порядков .Дифференцирование функции, заданной параметрически.
- •41. Теоремы Ролля, Лагранжа и Коши
- •42. Правило Лопиталя
- •Точная формулировка
- •Доказательство Отношение бесконечно малых
- •Примеры
- •43.Исследование функции на возрастание, убывание, экстремум.
- •44.Исследование функции на выпуклость, вогнутость и точки перегиба. Выпуклость функции и точки перегиба
- •45.Асимптоты: определение, классификация, нахождение.
- •46.План исследования функции
41. Теоремы Ролля, Лагранжа и Коши
Теорема 1. (Теорема Ролля) Пусть функция f(x)
непрерывна на отрезке [a, b];
дифференцируема в интервале (a, b);
на концах отрезка [a, b] принимает равные значения.
Тогда существует точка c (a, b) такая, что f'(c) = 0.
Доказательство приведено в книге И.М. Петрушко и Л.А. Кузнецова “Курс высшей математики: Введение в математический анализ. Дифференциальное исчисление.” М.: Изд–во МЭИ, 2000. Стр. 118.
Геометрическая интерпретация теоремы Ролля
Из теоремы Ролля следует, что существует точка с (a, b), в которой касательная к графику функции f(x) параллельна оси ОX (рис. 1).

Теорема 2. (Теорема Лагранжа) Пусть функция f(x)
непрерывна на отрезке [a, b];
дифференцируема в интервале (a, b).
Тогда существует точка с (a, b) такая, что
|
f(b) − f(a) = f '(c) · (b − a) . |
(1) |
Формула (1) называется формулой Лагранжа, или формулой конечных приращений
Доказательство приведено в книге И.М. Петрушко и Л.А. Кузнецова “Курс высшей математики: Введение в математический анализ. Дифференциальное исчисление.” М.: Изд–во МЭИ, 2000. Стр. 119.
Геометрическая интерпретация теоремы Лагранжа
Представим формулу (1) в виде
|
= f '(c) . |
(2) |
Число
f(b) − f(a) |
b − a |
есть угловой коэффициент прямой, проходящей через концы графика функции y = f(x) — точки (a, f(a) ) и (b, f(b) ), а f '(c) — угловой коэффициент касательной к этому графику в точке (c, f(c) ). Из формулы (2) следует, что существует точка с (a, b), в которой касательная к графику функции f(x) параллельна прямой, проходящей через концы графика (или совпадает с ней) (рис. 2).

Теорема 3. (Теорема Коши) Пусть функции f(x) и g(x)
непрерывны на отрезке [a, b];
дифференцируемы в интервале (a, b);
x (a, b) g'(x) ≠ 0 .
Тогда существует точка c (a, b) такая, что
|
=
. |
(3) |
Формула (3) называется формулой Коши.
Доказательство приведено в книге И.М. Петрушко и Л.А. Кузнецова “Курс высшей математики: Введение в математический анализ. Дифференциальное исчисление.
42. Правило Лопиталя
Правило
Бернулли[1]-Лопита́ля —
метод нахождения пределов
функций, раскрывающий
неопределённости вида ![]() и
и ![]() .
Обосновывающая метод теорема утверждает,
что при некоторых условиях предел
отношения функций равен
пределу отношения их производных.
.
Обосновывающая метод теорема утверждает,
что при некоторых условиях предел
отношения функций равен
пределу отношения их производных.
Точная формулировка
Условия:
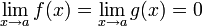 или
или 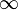 ;
;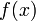 и
и 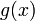 дифференцируемы
в проколотой окрестности
дифференцируемы
в проколотой окрестности 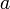 ;
;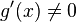 в
проколотой окрестности
;
в
проколотой окрестности
;существует
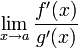 ,
,
тогда
существует ![]() .
.
Пределы также могут быть односторонними.
