33.Непрерывность функции в точке

Пусть функция f(x) определена в некоторой окрестности O(x₀) точки x₀ (включая саму точку x₀).

Функция f(x) называется непрерывной в точке x₀, если существует lim_x → x0 f(x) , равный значению функции f(x) в этой точке:

lim x → x0  f(x) = f(x0),

(1)

т.е.

 O( f(x0) )      O(x0) :     x  O(x0)  f(x)  O( f(x0) ) .

Замечание. Равенство (1) можно записать в виде:

lim x → x0  f(x) = f ( Lim x → x0 x ),

т.е. под знаком непрерывной функции можно переходить к пределу.

Пусть Δx = x − x₀ — приращение аргумента, Δy = f(x) − f(x₀ ) — соответствующее приращение функции.

Необходимое и достаточное условие непрерывности функции в точке.

Функция y = f(x) непрерывна в точке х₀ тогда и только тогда, когда

lim Δx → 0  Δy = 0.

(2)

Замечание. Условие (2) можно трактовать как второе определение непрерывности функции в точке. Оба определения эквивалентны.

Пусть функция f(x) определена в полуинтервале [x₀, x₀ + δ ).

Функция f(x) называется непрерывной справа в точке x₀, если существует односторонний предел

lim x → x0 + 0  f(x) = f(x0).

Пусть функция f(x) определена в полуинтервале (x₀ − δ, x₀].

Функция f(x) называется непрерывной слева в точке x₀, если существует односторонний предел

lim x → x0 − 0  f(x) = f(x0).

Классификация точек разрыва.

Условие (1) непрерывности функции f(x) в точке x₀ равносильно условию

f(x0 − 0) = f(x0 + 0) = f(x0),

(3)

где f(x ₀ − 0) = 

lim

x → x0 − 0

 f(x)   и   f(x₀ + 0) = 

lim

x → x0 + 0

 f(x) — односторонние пределы функции f(x) в точке x₀.

При нарушении условия (3) точка x₀ называется точкой разрыва функции f(x). В зависимости от вида нарушения условия (3) точки разрыва имеют различный характер и классифицируются следующим образом:

1. Если в точке x₀ существуют односторонние пределы f(x₀ − 0), f (x₀ + 0) и

f(x0 − 0) = f(x0 + 0) ≠ f(x0),

то точка х₀ называется точкой устранимого разрыва функции f(x) (рис. 1).

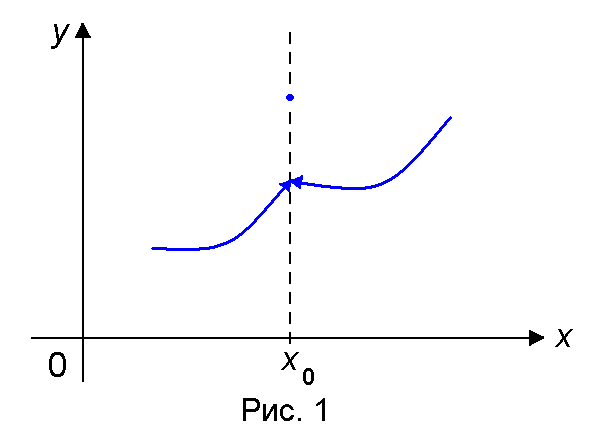
Замечание. В точке x₀ функция может быть не определена.

2. Если в точке x₀ существуют односторонние пределы f(x₀ − 0), f (x₀ + 0) и

f(x0 − 0) ≠ f(x0 + 0),

то точка x₀ называется точкой разрыва с конечным скачком функции f(x) (рис.2).

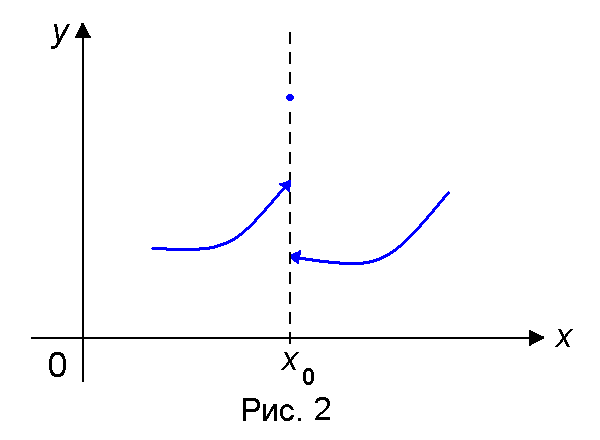
Замечание. В точке разрыва с конечным скачком значение функции может быть любым, а может быть и не определено.

Точки устранимого разрыва и конечного скачка называются точками разрыва 1–го рода. Их отличительным признаком является существование конечных односторонних пределов f(x₀ − 0) и f(x₀ + 0).

3. Если в точке x₀ хотя бы один из односторонних пределов f(x₀ − 0),  f (x₀ + 0) равен бесконечности или не существует, то x₀ называется точкой разрыва 2–го рода (рис. 3).

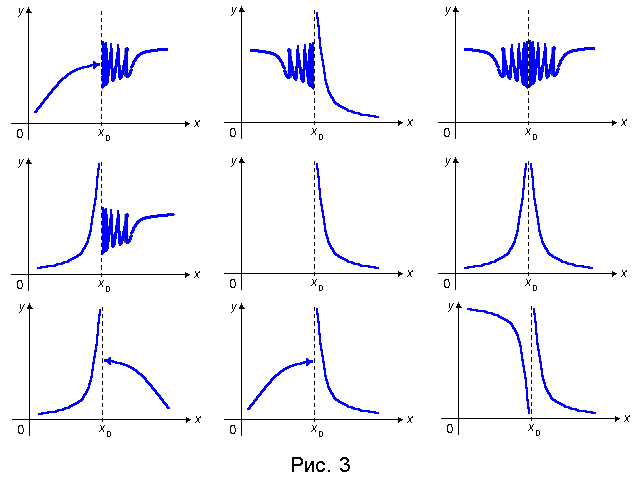
Если хотя бы один из односторонних пределов f(x₀ − 0),  f (x₀ + 0) равен бесконечности, то прямая x = x ₀ называется вертикальной асимптотой графика функции y= f(x).