12. Равномерная непрерывность.

Равномерная непрерывность – это свойство функции быть одинаково непрерывной во всех точках её области определения.

Функция называется равномерно непрерывной на подмножестве M X, если <0 >0 Q( Q_y

13. Производная. Касательная к кривой.

Производная функции y=f(x) в (.) х₀ называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю:

y’=lim_x→xo , или

Касательной к данной кривой в данной точке М называется предельное положение МТ секущей МА, проходящей через точку М, когда вторая точка пересечения А неограниченно приближена по кривой к первой точке.

14. Правило дифференцирования сложной функции.

Пусть y=f(u) и u=v(x), тогда y=f(v(x)) – сложная функция с промежуточным аргументом u и независимым аргументом х.

Теорема: если функция u=v(x) имеет производную u в точке х, а функция y=f(u) имеет производную y в соответствующей точке u=v(x), то сложная функция y=f(v(x)) имеет производную y в точке х, которая находится по формуле y = y u

Доказательство. По условию . Отсюда, по теореме о связи функции, её предела и бесконечно малой, имеем: = y +а где а→0 при →0, или = y +а . Функция u=v(x) имеет производную в (.) х: , поэтому u= +b , где b→0 при →0.

Подставив u в предыдущее равенство , имеем y ( +b )+а( +b ), т.е.

y + y b +а +аb , разделив на и перейдя к пределу при →0, имеем y = y u

15. Замена переменной в неопределённом интеграле.

Если f(x) непрерывна, то, полагая х=u(t), где u(t) непрерывна вместе со своей производной, получаем =

Таким образом, пусть требуется вычислить интеграл и удаётся найти функцию от х: t=u(x), чтобы подынтегральное выражение представилось в виде f(x)dx=g(u(x))u’(x)dx – более удобная форма для интегрирования, тогда достаточно найти интеграл , чтобы из него подстановкой получить искомый интеграл.

16. Теорема об обратной функции и её производной.

Производная обратной функции равна обратной величине производной данной функции.

y = , или

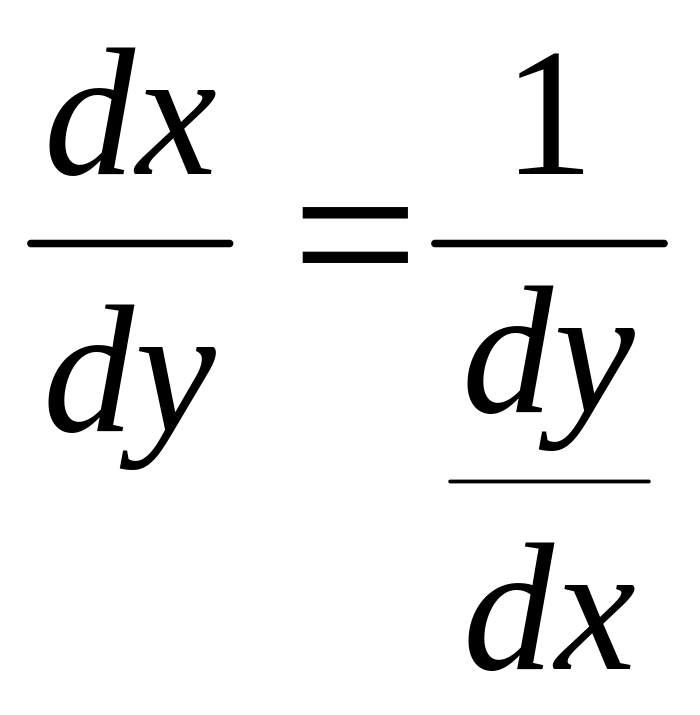
Рассмотрим обратную функцию x=u(y). Дадим аргументу приращение . Ему соответствует приращение Δх обратной функции, причём . Поэтому

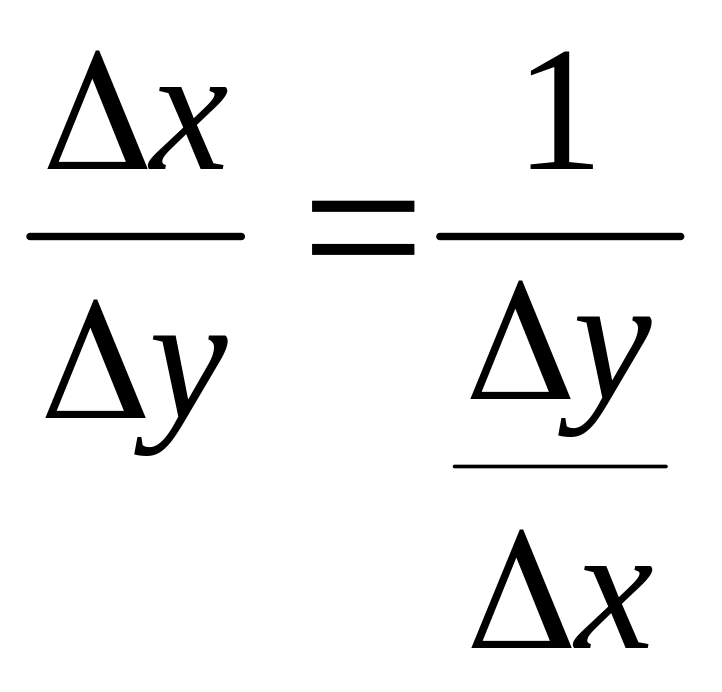
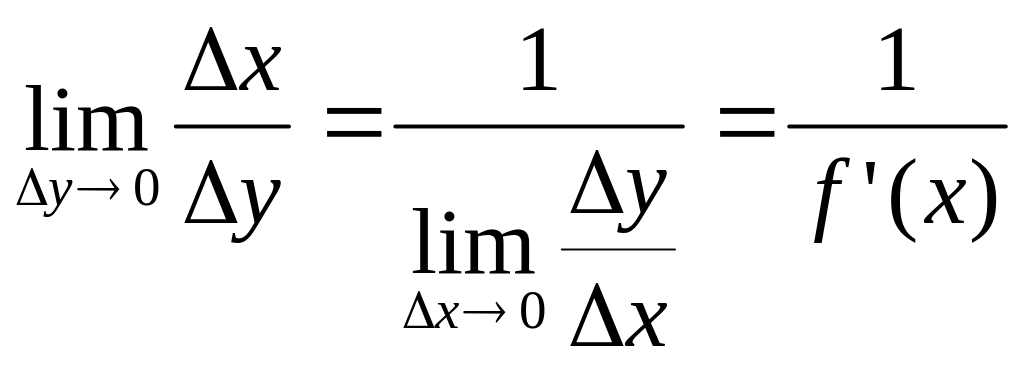Если Δу→0, то в силу непрерывности обратной функции приращение Δх!=0, и так так , то , т. е. y = ,

17. Дифференцирование произведения и интегрирование по частям.

(uv)’=u’v+v’u

Доказательство: Пусть y=uv. Тогда y’= = = = =v(x) +

+u(x) + =u’v+uv’+0u’=u’v+v’u

Интегрирование по частям: Пусть u=u(x) и v=v(x) – функции , имеющие непрерывные производные. Тогда d(uv)=udv+vdu. Интегрируя это равенство, получим:

= , или =uv -

18.Дифференцирование и интегрирование рациональных функций.

19. Теоремы Ролля и Лагранжа. Правило Лопиталя.

Теорема Ролля

Пусть 1)функция f(x) определена и непрерывна в замкнутом промежутке [a;b]; 2)существует конечная производная f’(x), по крайней мере, в открытом промежутке (a;b), 3)на концах функция принимает равные значения. Тогда между a и b найдётся такая (.) с, что f’(c)=0

Доказательство:

f(x) непрерывна в замкнутом промежутке, значит по теореме Вейерштрасса принимает в этом промежутке наибольшее М и наименьшее m значения. 1)если M=m, то f(x) в промежутке сохраняет постоянное значение, а тк (const)’=0, то f(x)=0. 2) M>m. Оба эти значения достигаются, причём на разных концах промежутка, значит хоть одно из них достигается в (.) с. Тогда, по теореме Ферма (о равенстве производной нулю в точке наибольшего (наименьшего) значения), f’(c)=0.

Теорема Лагранжа

Пусть 1) )функция f(x) определена и непрерывна в замкнутом промежутке [a;b]; 2)существует конечная производная f’(x), по крайней мере, в открытом промежутке (a;b). Тогда между a и b найдётся (.) с, такая, что .

Доказательство:

Введём вспомогательную функцию: F(x)=f(x)- (x-a)

Эта функция удовлетворяет всем условиям теоремы Ролля (она непрерывна, т.к. является разностью непрерывной и линейной функции. В промежутке (a,b) она имеет определённую конечную производную: F’(x)=f’(x)- и принимает равные значения на концах промежутка: F(a)=F(b)=0). Следовательно, к функции можно применить теорему Ролля: F’(c)=0. Таким образом, f(c)- =0, или f(с)= .

Правило Лопиталя

Если f(x)=y(x)=0 или f(x)=y(x)= , то = =а

Доказательство (по теореме Коши): , x→a=>c→a=> =