6. Использование систем массового обслуживания в планово-аналитической работе:

а)Понятие и классификация систем массового обслуживания. б)Одноканальные и многоканальные системы массового обслуживания с отказами. в)Многоканальная СМО с ожиданием в очереди при ограничении длины очереди. г)Основные показатели функционирования СМО.

а) Системы массового обслуживания (СМО) возникают тогда, когда про­исходит массовое появление заявок на обслуживание и их последующее удовлетворение. На производстве - это поступление сырья, материалов, по­луфабрикатов, изделий на складах и их выдача со складов; обработка боль­шой номенклатуры деталей на одном и том же технологическом оборудова­нии; организация наладки и ремонта оборудования; транспортные операции; планирование резервных и страховых запасов ресурсов широкого примене­ния; ввод и обработка информации в АСУ и многие другие.

Обслуживание заявок производят каналы (аппараты) обслуживания. При наличии одного канала СМО называется одноканальной; когда каналов не­сколько - многоканальной. Если несколько СМО соединены последовательно так, что заявки, обслуженные в одной СМО, переходят в следующую, то воз­никает многофазная СМО.

Обслуживание заявки в СМО продолжается некоторое случайное время, после чего освободившийся канал вновь готов к приёму заявки. Если в СМО допускается формирование очереди, то заявки, поступившие в моменты, ко­гда все каналы заняты, становятся в очередь и ожидают освобождения заня­тых каналов.

Работа СМО осложняется тем, что заявки поступают не регулярно, а сто­хастически, через случайные промежутки времени. Это приводит к тому, что в отдельные интервалы времени СМО работает с перегрузкой, в другие она недогружена или даже полностью простаивает.

При анализе и оптимизации СМО интерес вызывают усреднённые опе­рационные характеристики эффективности обслуживания: среднее число занятых (или простаивающих) каналов, коэффициент загрузки (или простоя) СМО, средний процент обслуживаемых (или получающих отказ) заявок, среднее время ожидания в очереди, среднее время пребывания в СМО, сред­няя длина очереди, средний доход от СМО в единицу времени, относительная и абсолютная пропускная способность системы и так далее.

Задача теории массового обслуживания - выявить зависимость показате­лей эффективности СМО от характера входящего потока; дисциплины и характера ограничения очереди; количества, производительности и условий функционирования каналов с целью последующей оптимизации СМО. В качестве критерия оптимальности применяют максимум прибыли от эксплуа­тации СМО; минимум суммарных потерь, связанных с простоем каналов, простоем заявок в очереди и уходом необслуженных заявок; обеспечение заданной пропускной способности СМО и т.п.

В качестве варьируемых при оптимизации переменных обычно фигури­руют количество каналов, их производительность, организация их работы в одноканальном или многоканальном режиме, условия взаимопомощи между каналами, дисциплина очереди, приоритетность обслуживания и другие.

Основными элементами СМО являются источники заявок, входящий по­ток заявок на обслуживание, каналы обслуживания, выходящий поток. Если источники заявок включены в СМО, она называется замкнутой, иначе - ра­зомкнутой. В зависимости от допустимости и характера формирования оче­реди различают:

1. СМО с отказами. Формирование очереди не разрешено, поэтому заяв­ка, пришедшая в момент, когда все каналы заняты, получает отказ и теряет­ся. Например: АТС, выполнение заказов к определённому сроку, поточные линии.

2. СМО с неограниченным ожиданием. Разрешается создание очереди неограниченной длины. Такая СМО обслуживает все заявки, хотя время ожидания обслуживания может оказаться очень большим.

3. СМО смешанного типа. Возможны различные ограничения, например, на максимальную длину очереди, на время пребывания заявки в очереди или системе и так далее. В СМО с ограничением длины очереди заявка полу­чает отказ, если она приходит в момент, когда все места в очереди заняты.

Заявка, попавшая в очередь, обязательно обслуживается. В СМО с ограниче­нием времени пребывания в очереди (СМО с "нетерпеливыми" клиентами) заявка ставится в очередь и ожидает некоторое случайное время. Если за это время она не попадает в канал обслуживания, то покидает очередь необслу­женной. В СМО с ограничением времени пребывания в системе заявка мо­жет получить отказ не только находясь в очереди, но и на обслуживании. Такой вариант СМО применяется для моделирования входного контроля заготовок и имитации брака на операциях при обработке деталей.

В СМО с очередью могут быть следующие варианты дисциплины посту­пления заявок из очереди на обслуживание:

- в порядке поступления (первым пришел - первым обслужили) - наибо­лее естественная дисциплина обслуживания;

- в порядке, обратном поступлению (последним пришел - первым обслу­жили); например, выемка деталей, заготовок из тары, бункера, склада, обра­ботка на ЭВМ самой последней информации и отбрасывание устаревшей ит.п;

- в соответствии с приоритетом; при поступлении заявки с более высоким приоритетом обслуживание заявки с низким приоритетом прерывается со­всем или на время обслуживания приоритетной заявки;

- в случайном порядке.

Важнейшим понятием в анализе СМО является понятие состояния систе­мы. Состояние есть некоторое описание системы, на основании которого можно предсказать ее будущее поведение.

б) Одноканальная система с отказами

Рассмотрим простейший случай, когда СМО имеет в своём распоряжении лишь один канал (п = 1) и работает с отказами. Проанализируем работу скла­да готовой продукции завода ЖБИ. Источниками заявок являются тележки с прицепами, подвозящие изделия на склад. Каналом обслуживания является кран. Граф состояний указанной системы показан на рис.1.

Рис.1. Граф состояний одноканальной системы с отказами. На рис.1 обозначено: Х₀ - состояние системы, когда канал не занят; р₀₀ - вероятность этого состояния; Xj - состояние системы, когда канал занят; Рп - вероятность этого состояния; Р_оь Р₁₀ - вероятность перехода системы из состояния в состояние. Вероятности перехода системы из состояния в состояние ха­рактеризуются матрицей перехода:

(1)

Естественно, что в начальный момент вектор вероятностей состояний системы имеет вид

(2)

Предположим, что поток требований тележек с прицепами, подвозящих изделия на склад, распределен по закону Пуассона

(3)

где Р_к - вероятность того, что за время t на склад поступит ровно "К" теле­жек с прицепами (заявок); К = О, 1, 2 ...; Я - плотность или интенсивность поступления тележек, т.е. среднее число тележек в единицу времени; t - отрезок времени, за который рассматривается отмеченная выше вероят­ность поступления тележек (заявок).

Вероятность того, что за время t не поступает ни одной тележки (К = 0), равна

(4)

Предположим, что время обслуживания одной тележки (заявки) распределено по показательному закону

(5)

где  - плотность или интенсивность обслуживания, т.е. среднее число заявок в единицу времени, определяется по формуле

(6)

где М t обсл - математическое ожидание.

Вероятность того, что за время At заявка будет обслужена, равна

(7)

При этом вероятность того, что за время t заявка не будет обслужена, равна

(8)

Сравнивая выражения (4) и (8) , заключаем, что время между двумя требованиями на обслуживание распределено по показательному закону. Указанное обстоятельство позволяет моделировать случайные моменты вре­мени поступления заявок на обслуживание и моделировать время обслужива­ния.

Выражения (4) и (7) могут быть преобразованы. Действительно, из математического анализа известно, что функция е^х может быть разложена в ряд Маклорена:

Раскладывая выражения (4) и (7) в ряд Маклорена и отбрасывая члены второго порядка, получаем

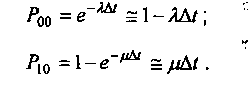(9) (10)

Подставив полученные значения вероятностей в формулу полной веро­ятности

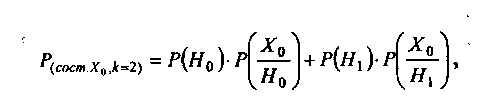
где Р(Н₀) - вероятность гипотезы о том, что после первого шага система была в состоянии Х₀ ; Р(Х0/Н₀) - условная вероятность события, состоящего в том, что за время второго шага система останется в состоянии Х₀ (Роо); P(H1)-вероятность гипотезы о том, что после первого шага система была в состоя­нии Xi; P(Xo/Hi) - условная вероятность события, состоящего в том, что за время второго шага система перейдет из состояния Xj в состояние Х₀ (Р10), получаем

(11)

или

(12)

Раскрывая скобки и группируя переменные, получаем

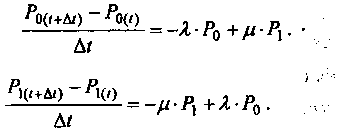(13,14)

Аналогично для

Выражения (13) и (14) называются разностными уравнениями. Пере­ходя к пределу при t 0, получаем систему дифференциальных уравнений, называемых уравнениями Эрланга:

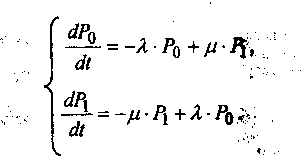(15,16)

Подобный переход системы из состояния в состояние называется процес­сом гибели и размножения. В теории массового обслуживания под рождени­ем подразумевают появление требования на обслуживание, а под гибелью - окончание обслуживания. Отмеченная система дифференциальных уравнений впервые была получена Эрлангом. Она является частным случаем системы дифференциальных уравнений Колмогорова.

Для установившегося режима производная равна нулю, поэтому система дифференциальных уравнений (15) и (16) преобразуется в систему алгеб­раических уравнений. В частности, для одноканальной системы массового обслуживания с отказами получаем

(17)

Рассматривая выражение (8), формируем следующее важное мнемони­ческое правило: "Что вытекает, то и втекает. Для каждого состояния сумма членов, соответствующая входящим стрелкам, равна сумме членов, соответствующих выходящим. Каждый член равен интенсивности потока событий переводящего систему по данной стрелке, умноженной на вероятность того состояния, из которого выходит стрелка".

Применительно к рассматриваемой одноканальной СМО с отказами ЭТО значит, что её перевод слева направо осуществляется с плотностью , а обратный переход справа налево осуществляется с плотностью .

Мнемоническое правило остаётся справедливым и для многоканальной системы с отказами и с ожиданием. Разрешая равенство (17) относительно р₀ и учитывая, что Р₀ +Р₁=1, получаем

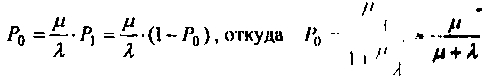(18)

При этом называется приведенной плотностью или загрузкой системы.

Многоканальная система с отказами

Предположим, что система функционирует с отказами и имеет в своём распоряжении n каналов (2).

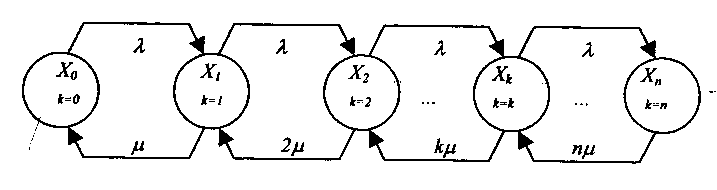
Рис.2. Граф состояний многоканальной системы с отказами Из графа состояний на рис. 2 видно, что перевод системы (где п - число каналов, к - число занятых каналов) слева направо осуществляется с плотно­стью , что обусловлено ординарностью потока заявок.

Ординарность - вероятность поступления более одного требования за ма­лый промежуток времени t есть величина более высокого порядка малости, чем t. Это свойство выражает практическую невозможность одновременно­го поступления двух или нескольких требований.

Обратный перевод системы справа налево осуществляется с суммируе­мой плотностью к (суммируются потоки от всех занятых каналов). Приме­няя мнемоническое правило «что вытекает, то и втекает», получаем:

1) если к=0,

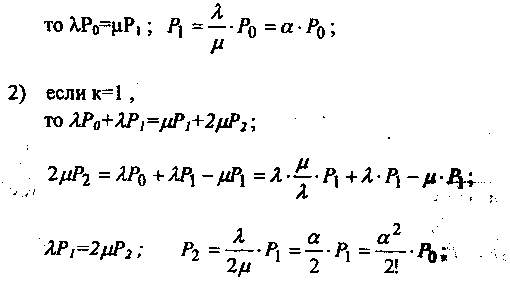
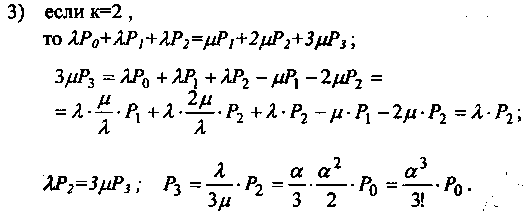
Аналогично для к = 3, 4, 5 и так далее. Применяя метод математической индукции, можно составить таблицу для приведенного правила "что вытека­ет, то и втекает" и написать выражения для определения системы при к = 1,2,...,« (табл. 1).

Таблица 1

Вероятности состояний многоканальной СМО, функционирующей с отказами

Число заня­тых каналов	Приведенное правило: "Что вытекает, то и втекает"	Вероятность состояний для многоканальной системы с отказами
К = 0	Р0=Pi	P1=aP0
К= 1	Р1=2Р2	Р2=α/2*Р1=α2/2!*Р0
К = 2	Р2=ЗР3	Р3=α/3*Р2=α3/3!*Р0
…	…	…
К-1	Pк-1=kPk	Рк=α/к*Рк-1=αк/к!*Р0
…	…	…
п-1	Pn-1=nPn	Рn=α/n*Рn-1=αn/n!*Р0

Сумма вероятностей всех состояний должна быть равна единице, поэтому

в) Многоканальная СМО с ожиданием в очереди при ограничении длины очереди

Рассмотрим СМО, когда прибывшая заявка в случае, если все каналы к моменту ее прибытия заняты, не покидает пост, а становится в очередь. Заяв­ка может стать в очередь только при условии, что имеется место для ожида­ния. В противном случае заявка покидает очередь.

Проиллюстрируем порядок вычисления числовых характеристик "функ­ционирования СМО для заданных условий. Предположим, что система имеет в распоряжении "я" каналов и "m" мест для ожидания в очереди. После того, как все места для ожидания в очереди заняты, прибывшая заявка получает отказ и немедленно покидает очередь. Из графа состояний системы, показан­ного на рис.4, видно, что, включая состояние Хn, очереди нет. Затем воз­никает очередь.

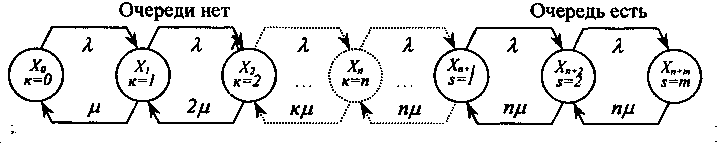
Рис.4. Граф состояний многоканальной СМО с ожиданием в очереди с 1 ограничением длины очереди (S - число занятых мест)

Поток, переводящий систему слева направо, определяется плотностью . Что касается потока событий, переводящего систему справа налево, то до возникновения очереди он равен , 2, 3,..,п. После возникновения оче­реди указанный поток остаётся постоянным и равным п.

Пользуясь правилом "что втекает, то и вытекает", можно вычислить ве­роятности состояний системы до возникновения очереди (табл.2) и после возникновения очереди (табл.3).

Сумма вероятностей всех состояний системы должна быть равна единице, т.е.

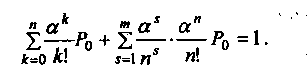
Отсюда

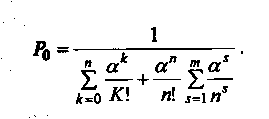
Поясним порядок вычисления вероятностей состояний СМО с ожиданием в очереди при ограничении длины очереди на примере.

Таблица.2

До возникновения очереди

После возникновения очереди

19