2. Оценка достоверности корреляционно-регрессионного моделирования и возможности практического использования полученных моделей:

а)Оценка репрезентативности выборочной совокупности данных. б)Расчет критериев Стьюдента для коэффициентов корреляции и регрессии. в)Определение ошибки аппроксимации. г)Расчет коэффициента детерминации. д)Определение коэффициентов эластичности для факторов – аргументов.

Ответ: а) При исследовании корреляционной зависимости всегда приходится анализировать не всю генеральную совокупность исходных данных, а только лишь выборку, как правило, случайную. Следовательно, и рез-ты расчетов, полученных на эой основе, характеризуют зависимости, свойственные конкретной выборке. Исследователя интересует достоверность или существенность полученных на основе данной выборки результатов, которая оценивается величиной вероятности того, что эти рез-ты явл. не случайными по отношению ко всей генеральной совокупности. Принято считать, что при значениях вероятности в пределах 0,95-0,99 полученные рез-ты расчетов корреляционного анализа явл. достоверными. Величина такой вероятности определяется значением специального критерия t.

б) Расчет критериев Стьюдента для коэффициентов корреляции и регрессии.

Для получения в процессе анализа коэф. корреляц.(r) критерий (t_p^r) рассчитывается по формуле t_p^r=r/_r, где величина ошибки коэф. корреляц. (_r) =(1-r²)/√n.

Если t_p^r >(либо=)t_t, то рез-т достоверный.

Расчет критерия (t_p^b), характеризующего достоверность коэф. регрессии (b), производится по формуле: t_p^b= b/_b, где _b=(σ_y*√1-r²)/(σ_x*√n), где σ_y и σ_x – среднеквадратическое отклонение фактических значений Y и X соответственно от их средних значений (σ_y=√(y-y^ср)²/√n). Если критерии меньше табличного значения, то достоверность полученных коэф. не доказана, следует отказаться от фактора-аргумента, или расширить выборку, т.е. увеличить число наблюдений.

в) Определение ошибки аппроксимации.

Для оценки адекватности рассчитывается ошибка аппроксимации (γ).

γ=(√1/n*(y_x-y)²)/(у^ср)*100, где у_х – значение ф-ии, определяемое по уравнению регрессии для каждого фактического значения аргумента; у, у^ср – фактическое и среднеарифметическое значение ф-ции. Величина коэффициента показывает размер средней ошибки замены (аппроксимации) фактических значений функции значениям функции, вычисленными по уравнению регрессии.

г) Расчет коэффициента детерминации.

D=100*r², используется для оценки доли влияния факторов, включенных в модель, на изменчивость функции.

д) Определение коэффициентов эластичности для факторов – аргументов.

Коэф. эластичности показывает на сколько в среднем изменится значение у при изменении х на 1, определяется Э=b*x_i^ср/у^ср.

3. Парная и множественная корреляция:

а) Сущность парной корреляционной связи. б) Натуральный и стандартизированный масштаб данных. в) Оценка мультиколлинеарности факторов – аргументов исследуемой зависимости в множественной корреляционной модели.

Особенности множественной корреляции

В силу особенностей корреляционной зависимости, которая характеризу­ется одновременным воздействием на функцию не одного аргумента, а не­скольких, особый интерес и практическую ценность приобретает изучение корреляции многих переменных.

Множественная корреляция изучает зависимость между функцией и ря­дом аргументов. Уравнение множественной корреляции переменных, имею­щее линейный характер, в натуральном масштабе имеет следующий вид:

где у - значение функции, соответствующее заданным значениям аргументов; bi - коэффициенты при неизвестных или коэффициенты регрессии; xi,- - факторы-аргументы, влияющие на функцию.

При исследовании множественной корреляции используется метод, в ко­тором все переменные и соотношения между ними выражаются в стандарти­зованном масштабе. В этом масштабе за начало отсчета для каждой перемен­ной принимается значение ее среднего арифметического, а за единицу изме­рения - величина среднего квадратического отклонения. Уравнения множест­венной корреляции в стандартизованном масштабе имеют вид:

где t - стандартизованное значение переменных у, л;, значение которых опре­деляется по формуле (например, для х)\

 - стандартизованные коэффициенты при переменных.

Численное значение параметров уравнения множественной корреляции в натуральном () и стандартизованном () масштабах определяется методом наименьших квадратов. Коэффициенты регрессии в натуральном масштабе несопоставимы, т.к. характеризуют вариацию функции при изменении на единицу различных по природе факторов, измеренных обычно в различных единицах. Коэффициенты регрессии в стандартизованном масштабе можно соизмерять и, следовательно, ранжировать факторы по силе их воздействия на изменчивость функции.

При изучении корреляции многих переменных теснота связи между функцией и всеми включенными в модель факторами-аргументами характе­ризуется коэффициентом множественной корреляции (R). Его значение нахо­дится в пределах 0 < R < 1.

Коэффициент множественной корреляции используется часто в качестве критерия при выборе окончательного варианта модели. В процессе исключе­ния из модели или включения в нее дополнительного фактора R уменьшается или увеличивается. Величина изменения его позволяет сравнить модели и оценить весомость исключенного или дополнительно введенного фактора.

Часто для оценки доли влияния факторов, включенных в модель, на из­менчивость функции определяется коэффициент детерминации D.

1 - R² - коэффициент остаточной детерминации, характеризующий долю влияния на изменчивость функции остальных, не включенных в модель фак­торов.

Примеры моделирования методами математической статистики

Пример 1. Выбор по статистическим параметрам* варианта модели «Зави­симость сдачи продукции с первого предъявления от коэффициента ритмич­ности и величины сверхплановых потерь рабочего времени». Исходные дан­ные приведены в табл. 2.6.

Были получены следующие модели:

1. Y =А₀ +A₁X₁ + А2Х₂

2. y = a_o + a₁x₁+ А₂²

3. Y =A₀ +А₁ X₁²+A₂X₂²

4.Y = Ао + А₁ Х₁² +А₂Х₂;

5.Y = A₀+A1X1++A₂/X₂.

Параметры, характеризующие эти модели приведены в табл. 2.7

Для доверительной вероятности 95% при 22 степенях свободы табличное значение Т-критерия равно 2,074. По этому критерию первая и четвертая модели имеют значимые коэффициенты регрессии в натуральном масштабе. Для этой же доверительной вероятности и степеней свободы соответственно 22 и 2 табличное значение F-критерия равняется 3,44. По этому критерию множественные коэффициенты корреляции всех моделей значимы, т.к.

F расч > Fтабл.

Наибольшую величину множественного коэффициента корреляции име­ют модели первая и четвертая. Таким образом первая и четвертая модели по формальным признакам можно считать равноценными. Однако первая модель значительно удобнее четвертой при ее использовании, так как обе перемен­ные линейные.

Таблица 2.6

Исходные данные

Номер наблюдения	Коэффициент ритмичности Хг	Сверхплановые потери рабочего времени, % Х2	Сдача продукции с первого предъявле­ния, % Y
1	0,84	2,0	96,53
2	0,83	2,3	97,21
3	0,87	1,2	97,75
4	0,90	5,4	95,8
5	0,82	2,4	96,47
6	0,88	3,2	96,6
7	0,87	1,9	97,84
8	0,90	3,0	96,58
9	0,89	4,0	97,11
10	0,86	з,з	96,62
11	0,90	2.9	96,7
12	0,96	4,3	96,25
13	0,89	4,0	97,15
14	0,87	1.9	97,2
15	0,87	2,1	97,34
16	0,85	1,1	97,89
17	0,88	0,5	98,64
18	0,85	1,2	98,66
19	0,83	2,4	97,2
20	0,87	1,3	98,31
21	0,82	1/7	97,52
22	0,86	2,0	97,1
23	0,83	1,95	97,9
24	0,96	2,96	98,12
25	0,97	2,5	97,71
средние	0,875	2,46	97,29

Таблица 2.7

Параметры моделей

Параметры	Номер модели
	1	2	3	4	5
Коэффициенты регрессии в нату­ральном масштабе ао А, А2	93,27 6,26 -0,60	93,1 5,56 -0,09	95,6 3,0 -0,09	96,12 3,42 -0,59	95,3 1,41 1,42
Расчетные значения Т-критериев Та0 Та, Та2	43,79 2,47 6,45	37,52 1,92 5,16	79,96 1,85 5,12	94,92 2,4 6,42	37,11 0,489 4,32
Коэффициенты регрессии в стан­дартизованном масштабе Pi 02	0,35 -0,90	0,31 -0,83	0,29 -0,82	0,34 -0,9	0,078 0,69
Коэффициент множественной корреляции R	0,8116	0,7426	0,739	0,8	0,6788
Значение F-критерия (FРасч)	21,23	13,52	13,23	20,78	9,4

Пример 2. Анализ затрат на рубль товарной продукции в зависимости от выпуска продукции в 3 декаду и % сдачи продукции с 1-го предъявления.

Исходная информация приведена в табл. 2.8. Форма связи выбрана ли­нейная.

Характеристики исходных данных и параметры модели приведены ниже. Средние значения: Х1 =58,4l; Х2 =95,785; Y = 0,866.

Средние квадратические отклонения: σ_xl = 8,53; σ_х2 = 1,26; σ_у = 0,049.

Парные коэффициенты корреляции:

r_x1x2 = -0,45; r_x1y = 0,74; r_x2y=-0,57.

Таблица 2.8

Исходная информация

Номер наблю­дения	Выпуск продукции в 3 декаду, % *i	Сдача продукции с 1-го предъявления, % Х2	Затраты на 1 рубль товарной продукции, Y,py6.
1	72,9	92,0	0,96
2	44,3	98,5	0,79
3	34,2	96,2	0,77
4	59,8	96,3	0,85
5	69,1	95,0	0,96
6	58,5	96,5	0,84
7	48,8	95,4	0,84
8	56,8	95,9	0,85
9	60,7	95,9	0,82
10	56,0	96,6	0,90
11	51,0	95,9	0,81
12	38,0	95,4	0,81
13	61,7	95,1	0,89
14	63,8	95,8	0,93
15	57,1	97,0	0,84
16	57,0	96,3	0,84
17	53,0	96,3	0,88
18	63,7	95,0	0,85
19	58,0	96,6	0,82
20	70,1	93,9	0,88
21	59,0	95,2	0,83
22	66,5	96,3	0,89
23	56,8	97,1	0,89
24	57,3	96,2	0,83
25	50,8	96,4	0,83
26	60,4	94,3	0,91
27	60,1	96,4	0,86
28	65,2	96,0	0,91
29	60,1	96,8	0,87
30	65,9	96,3	0,92
31	56,5	95,7	0,83
32	68,2	96,3	0,86
33	66,2	92,3	0,98

Частные коэффициенты корреляции r_x1y(_x2)⁼ 0,66; r_x2y(_x1) = -0,39.

Уравнение регрессии в стандартизованном масштабе t_y = 0,61t_x1-0,29t_x2.

Уравнение регрессии в натуральном масштабе Y = 1,74 + 0,0035X₁ - 0,011Х₂. Множественный коэффициент корреляции: R = 0,8.

Расчетные значения T-критериев: Т_а0 = 3,55; Т_а1 = 4,88; Т_а2 = 2,31.

Расчетное значение F-критерия для степеней свободы 2 и 30:

F_расч = 24,34.

Проверим соответствие исходной информации нормальному распределе­нию по табл. 2.9. Таблица 2.9 Проверка информации на нормальность

	Максималь-	Минималь-	Размах	Стандарт-	Размах
Переменные	ное значе-	ное значе-		ное откло-	станд. от-
	ние	ние		нение	клонения
Xi	72,9	34,2	38,7	8,53	4,54
Х2	98,5	92,0	6,5	1,26	5,16
Y	0,98	0,77	0,21	0,049	4,29

Сравнение расчетных значений с критическими границами отношения размаха к стандартному отклонению позволяет утверждать с вероятностью ошибки в 1% и ниже, что распределение совокупности данных соответствует нормальному.

Парные и частные коэффициенты корреляции подтверждают наличие связи между факторами-аргументами и функцией. Поскольку частные коэф­фициенты незначительно отличаются от парных, то можно полагать, что связь между Х₁ и Х₂ не приведет к искажению модели.

По величине коэффициента детерминации, равному R² = 0,64, можно су­дить о совокупной доле влияния факторов, включенных в модель, на затраты на 1 рубль товарной продукции. Остальная часть - 0,36 или 36% приходится на другие факторы. Рассматривая коэффициенты регрессии в стандартизо­ванном масштабе, видим, что ₁ > ₂ в 2,Граза, т.е. фактор X₁ в 2,1 раза силь­нее влияет на изменчивость У, чем фактор Х₂.

Действительно, улучшение ритмичности приводит к устранению допол­нительных затрат, связанных с браком и сверхурочными работами, и к увели­чению выпуска продукции. Все это через прямые и косвенные затраты отра­жается на удельном показателе себестоимости.

Увеличение сдачи продукции с первого предъявления приводит к увели­чению выпуска продукции и, как следствие этого, к сокращению удельных затрат. Однако рост Х₂, особенно в области, близкой к 100%, требует выпол­нения комплекса мероприятий, затраты на реализацию которых могут при­вести и к увеличению затрат на 1 рубль товарной продукции.

Коэффициенты регрессии достоверны по критерию Стьюдента, а надеж­ность модели подтверждается и по F-критерию: F_расч > F_табл = 3,32 для дове­рительной вероятности 95%.

Уравнение регрессии в натуральном масштабе можно использовать для выявления резервов снижения себестоимости при раздельном и одновремен­ном изменении Х₁ и Х₂. Изменения могут быть различными: на определенную абсолютную или относительную величину, в интервале изменения и т.п. в соответствии с целью анализа. Например, если в уравнение подставить наи­лучшие достигнутые значения Х₁ = 34,2 и Х₂ = 98,5, суммарный резерв сни­жения себестоимости относительно средней величины затрат на 1 рубль то­варной продукции составит около 11 коп., или 12,6%. Конечно базой для сравнения может быть и другой уровень затрат: максимальный, минималь­ный, соответствующий какому-либо наблюдению и т.п.

Таким образом, анализ показывает, что в первую очередь необходимо со­средоточить внимание на улучшении ритмичности производства, т.к. средний выпуск продукции в 3 декаду далек от теоретической величины, равной 33,4%. Кроме того, улучшение ритмичной работы, как показывает опыт, тре­бует принятия организационных мер, обычно не сопровождающихся дополнительными затратами, в отличие от мероприятий, направленных на увеличе­ние сдачи продукции с первого предъявления.

Пример 3. Исследование зависимости себестоимости единицы продукции от технологических факторов.

Особое значение для изы­скания резервов дальнейшего снижения себестоимости еди­ницы продукции играет все­сторонний и глубокий анализ зависимости ее уровня от та­ких показателей, как часовая производительность оборудо­вания, степень использования сырья и т.д.

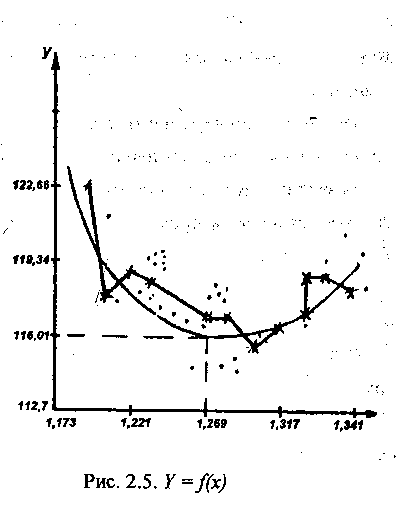
Для установления и коли­чественного определения та­ких зависимостей был прове­ден корреляционный анализвлияния часовой производи­тельности прокалочных печей (X) на себестоимость 1 т монохромата натрия (Y). Построенное поле кор­реляции и эмпирическая линия регрессии (рис. 2.5) подтверждают параболи­ческую форму связи между Y и X.

Получена модель: Y = 1466,06-2107,43Х+ 822,52Х².

Теоретическая линия регрессии, представляющая собой параболу второго порядка, изображена на рис. 2.5. Математический анализ полученного урав­нения позволил установить оптимальное значение часовой производитель­ности печей (X = 1,271 т/ч), при котором себестоимость одной тонны моно­хромата натрия достигает своего минимума (Y_min = 115,89руб.).

Для этого необходимо первую производную приравнять нулю:

Y'_x = -2107,43 + 2 - 822,52 X = О, X = 2107,43 /1645,04 = 1,271.

Коэффициент парной корреляции, равный 0,56, свидетельствует о нали­чии достаточно тесной связи между выбранными факторами, а критерий Стьюдента Т_р = 5,6 значительно превышает его табличное значение. Ошибка аппроксимации, равная 4,3%, свидетельствует об адекватности полученного уравнения.

Результаты проведенного анализа могут быть использованы для установ­ления часовой производительности оборудования в оптимальных пределах, что позволит снизить себестоимость единицы продукции. Кроме того, опти­мальное значение часовой производительности может быть заложено в осно­ву расчета производственной мощности.