4.1.1 Теоретические основы сушки. Тепло- и массообмен при сушке

Сушкой называют термический процесс удаления влаги из твердых материалов путем ее испарения. Про­цесс сушки изделий и материалов сопровождается изме­нением объема, которое называют усадкой. За счет удаления влаги частицы материала сближаются и размеры материала или изделия уменьшаются. При изменении объема (усадке) материал деформируется, возможны коробление и растрескивание изделий.

Классификация форм связи (воды) влаги с материалом (по П.А. Ребиндеру)

1. Химически связанная (кристаллизационная) – входит в состав кристаллических решеток материалов. Ее удаление сопровождается разрушением кристаллических решеток. Процесс возможен при высоких температурах, следовательно, требует большего количества энергии для разрушения связей.

Если материал поглощает жидкость, которая химически связанная, то возможна контракция.

2. Физико-химическая:

а) адсорбционно-связанная – адсорбируется на внешней поверхности под действием силового поля коллоидных частиц (мицелл). С поверхности мицелл влага может проникать внутрь мицеллы и образовывать в ней интрамицеллярный слой.

б) осмотически связанная влага – проникает в скелет (влага набухания) коллоидного тела, который состоит из замкнутых клеток. Влага проникает через стенки клеток путем избирательной диффузии за счет сил осмотического давления.

Удаление адсорбционно-связанной и осмотически связанной влаги возможна при t≤100^оС.

3. Физико-механическая - заполняет макро- и микрокапилляры (макро- с r >10^-5 см); к физико-механической относится влага смачивания.

Макрокапиляры - такие капилляры не сорбируют влагу из воздуха и заполняют только при непосредственном соприкосновении с влагой.

Микрокапилляры - с r<10^-5 см вследствие сил капиллярного давления могут заполнятся влагой за счет сорбции ее из воздуха, а также при ее конденсации на поверхности материала.

Влага смачивания связывается с материалом при прямом соприкосновении. Эта связь непрочна и нарушается при воздушном хранении.

Влажное состояние материала в процессе сушки. Количественными характеристиками влажностного состояния материала является относительная и абсолютная влажность, или влагосодержание. Относи­тельная влажность W_от представляет отношение массы воды ко всей массе влажного материала, а абсолютная влажность W_аб — отношение массы воды к сухой массе материала. Оба параметра выражаются в процентах. Влагосодержанием материала U называют отношение массы воды к сухой массе материала, выраженное в до­лях единицы.

По отношению к окружающему воздуху различают:

- равновесное;

-гигроскопическое;

-влажное состояния ма­териала.

Влажное - парциальное давление водяного пара на поверхности выше, чем давление воздушных паров в окружающей среде. При максимальных условиях материал отдает влагу.

Равновесное - парциальное давление водяного пара на поверхности равно давлению воздушных паров в окружающей среде.

Гигроскопическое - парциальное давление водяного пара на поверхности ниже, чем давление воздушных паров в окружающей среде. В данном случае, материал соргирует влагу из окружающей среды и постепенно переходит в равновесное.

Физическая сущность этих состояний раскрыва­ется изотермами сорбции (десорбции) влажного мате­риала, устанавливающими зависимость между его рав­новесным влагосодержанием U_p и относительной влаж­ностью φ окружающего воздуха. Сорбция — поверхностное поглощение влаги материалом, десорбция — отделение влаги через поверхность материала.

Знание равновесного состояния имеет важное значение. Разработаны методики для определения равновесного состояния, которые предусматривают помещение материала в воздушную среду с определенной температурой и определенным парциальным давлением водяных паров. Иногда просто материал хранят в окружающей среде с определенной влажностью и затем замеряют его влагосодержание.

Очевидно, что с увеличением температуры хранения материала в равновесном влагосодержании понижается (t_хран↑→ W_равн↑).

Испарение влаги из материала начинается с поверхностей и поэтому неизбежен перепад влагосодержаний между центром и поверхностями. Перепад же влагосодержаний ΔU ведет к возникновению градиента потенциала переноса влаги ∇U, который заставляет влагу продвигаться к поверхности. Возникновение перехода влагосодержаний обусловлено тем, что скорость испарения больше скорости диффузии влаги к поверхности [3].

;

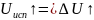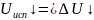
Кинетика процессов сушки влажных материалов. Подвергнутый сушке материал под воздействием су­шильного агента отдает влагу с открытых поверхностей. Изменение влагосодержания материала во времени вы­ражают графически. Этот график называют кривой суш­ки. На рис. 4.1 показана характерная для капиллярно-пористого коллоидного материала кривая сушки / и кри­вая, характеризующая температуру материала 2 в процессе сушки. Пунктиром на рисунке обозначены: под­держиваемая постоянной температура сушильного агента по сухому t_c и мокрому t_м термометрам. Также пунктир­но дана и Up — линия равновесной влажности материала по отношению к сушильному агенту.

Материал со средним влагосодержанием U₀ и температурой t₀ помещается в установку, через которую прохо­дит сушильный агент с t_c>t₀ и парциальным давлением водяных паров Р'_сa, которое меньше, чем парциальное давление водяных паров на поверхности материала Р'_пм. Материал начинает отдавать влагу (смотреть кривую 1), су­шильный агент ассимилирует ее, насыщается и удаляет­ся из установки. Взамен отработанного поступают все время новые порции сушильного агента. Количество вла­ги, удаляемое в единицу времени из материала, начина­ет возрастать, и в точке а' на кривой 1 достигает макси­мума. Одновременно температура материала повышается от t₀ до t_м в точке а' и поверхность материала достигает точки росы — температуры сушильного агента по мокро­му термометру.

Рис. 4.1. Изменение среднего влагосодержания (кривая сушки) и температу­ры тела во времени, в процессе сушки при постоянной температуре

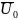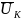и — среднее начальное и конечное влагосодержание тела; U_p— рав­новесное влагосодержание тела; t_c и t_м —температура сушильного агента по сухому и мокрому термометру; t_п — температура поверхности тела; t_ц — температура центра тела; кривая 1 — линия изменения среднего влагосодер­жания тела в процессе сушки; кривая 2 — то же для температур тела; τ₁, τ₂, τ₃ — продолжительность периодов сушки; τ_к — возможное время оконча­ния сушки; 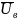t_nв, t_цв —соответственно среднее влагосодержание, темпе­ратура поверхности и температура центра тела к моменту времени τ_к.

Период возрастающей влагоотдачи с одновременным нагревом поверхности материала до точки а' называют первым периодом сушки. Он очень кратковременный, его продолжительность показана линией, отсекающей на оси времени отрезок, обозначенный τ. От точки а влагосодержание начинает уменьшаться с одинаковой скоро­стью до точки б, при этом температура поверхности ма­териала не меняется, что объясняется испарением влаги с поверхности, а такой процесс идет с расходом теплоты на парообразование. В этот период температура в цент­ре материала постепенно повышается до температуры поверхности. Этот период, который показан на кривой 1 от точки а до точки б, называют периодом постоянной скорости сушки.

Точка б, характеризующая окончание периода посто­янной скорости сушки, как показали исследования, одно­временно соответствует критическому влагосодержанию материала.

Под ним понимают такое состояние материа­ла, когда заканчивается его усадка, а следовательно, практически завершаются и процессы структурообразования. Продолжительность периода обозначена на оси времени отрезком τ₁ – τ₂ .От точки б на кривой 1 до сред­него конечного влагосодержания , которое характерно для выгружаемого из установки материала, процесс уда­ления влаги замедляется, и кривая 1 асимптотически приближается к 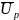—равновесному влагосодержанию. Это так называемый период падающей скорости сушки — третий по порядку. Третий период сушки самый продол­жительный. И чем ближе влагосодержание равновес­ному, тем продолжительнее он становится. Начало пери­ода падающей скорости сушки (точка б на кривой 1) на кривой температуры материала 2 характеризуется точкой б. В этой точке начинает резко возрастать температура по­верхности материала t_п, которая в третьем периоде асимптотически приближается к температуре сушильного аген­та по сухому термометру. Одновременно за счет тепло­проводности начинает прогреваться и центр материала, его температура также возрастает. Продолжительность периода обозначена отрезком [τ₃— (τ₂+ τ₁)].

Физический смысл повышения температуры, поверхно­сти материала, начиная с точки б', заключается в следу­ющем. К этому времени общее влагосодержание мате­риала уменьшается, влага к поверхности для испарения подается медленно, поверхность испарения «передвигается» внутрь материала. Пар образуется уже не на поверхности, а на каком-то расстоянии от нее, в глубине материала и, диффундируя через слой в окружающую среду, покидает материал и ассимилируется сушильным агентом. Поэтому из-за отсутствия испарения на поверх­ности ее температура начинает резко возрастать. Повы­шение температуры поверхности t_п влечет за собой про­грев центральных слоев материала и температура в цент­ре t_п также возрастает.

Обычно процесс не ведут до и материал выгружа­ют раньше, чем закончится третий период тз. Например, проведем через линию KN, перпендикулярную оси τ, и будем считать всю продолжительность сушки равной τ_к. Тогда выгружаемый из установки материал будет иметь среднее влагосодержание 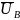, температуру на поверхности t_пв и температуру в центре t_цв. Следова­тельно, зная необходимое конечное среднее влагосодер­жание материала по снятому с натуры графику измене­ния влагосодержания и температур можно судить о про­должительности и характере реального процесса сушки.

Материалам с различным характером связи влаги соответствуют и свои кривые сушки, однако общий ха­рактер кривой и ее деление на три периода характерно для всех коллоидно-капиллярнопористых материалов, к каким относятся строительные изделия. Кроме кривой сушки иногда строят и кривую скорости сушки во време­ни du/dr = f(τ). Ее получают путем графического диффе­ренцирования кривой сушки. Кривую скорости сушки можно определить и другим способом. Для этого кривую сушки делят на равные участки ∆τ и находят убыль вла­ги Aw на каждом из этих участков по отношению к выб­ранной продолжительности сушки на участках ∆τ.

Остановимся на понятии критическое влагосодержа­ние. Известно, что материал, отдавая влагу, сокращает­ся в размерах. В это время формируется структура мно­гих материалов, образуются поры и капилляры. Усадка (сокращение размеров) идет только до какого-то опре­деленного влагосодержания. Дальнейшее его снижение усадки не вызывает. Поэтому обычно устанавливали вла­госодержание, при котором усадочные явления в мате­риале заканчивались. Это влагосодержание для каждо­го конкретного материала свое и было названо критиче­ским. Существовало мнение, что после достижения критического влагосодержания материал можно сушить как угодно быстро. При этом из-за отсутствия усадки ма­териал не должен был растрескиваться. Однако, как по­казала действительность, в некоторых случаях он все-таки растрескивался.

С развитием теории сушки было установлено, что кри­тическое влагосодержание непостоянно даже для одного и того же материала, оно зависит от режимов сушки. Если считать исходным определенное критическое влаго­содержание 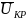, полученное из опыта, то оказывается, что при более быстрой сушке критическое влагосодержа­ние будет иным — 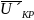(для данного опыта), станет вы­ше, т. е. > и наоборот, при более медленной сушке критическое влагосодержание для этого же мате­риала 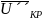станет меньше , т. е. < . Эту зави­симость необходимо помнить и пользоваться ею, опреде­ляя режимы сушки изделий [5].

Усадочные явления и деформации в процессе сушки. В процессе сушки керамических и ряда теплоизоляци­онных материалов не только уменьшается влагосодержа­ние материала, но и происходят процессы структурообразования. В первую очередь они вызываются сокраще­нием размеров материала. При удалении влаги частицы материала сближаются и общие размеры материала сокращаются. Для подавляющего большинства материалов объемная усадка подчиняется линейному закону. Зави­симость между объемом тела V и его влагосодержанием U описывается формулой

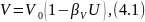
где 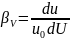- коэффициент объемной усадки.

В капиллярно-пористых коллоидных телах, т. е. в строительных материалах, и линейная усадка происходит по аналогичному закону

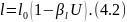
В этом случае 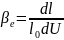- коэффициент линейной усадки, характеризующий интенсивность изменения ли­нейных размеров материала.

Усадка зависит от молекулярной структуры вещества и от видов связи влаги с материалом. Однако из-за разного влагосодержания по сечению усадка в мате­риале будет различной, что приводит к развитию объемно-напряженного со­стояния и, как следствие, к нарушению структуры— растрескиванию. Следова­тельно, основное препят­ствие для быстрой суш­ки —растрескивание, а иногда и полное разруше­ние материала.

Возникновение объем­но-напряженного состоя­ния по А. В. Лыкову за­ключается в неравномер­ном распределении влаго­содержания. Для поясне­ния рассмотрим сушку ма­териала в виде пластины длиной l_о, см. рис. 4.2. Предположим, что сушка происходит только с двух сто­рон (одномерное поле), остальные поверхности пласти­ны влагоизолированы. Процесс происходит в изотерми­ческих условиях при температуре, равной температуре пластины.

Рис. 4.2. Напряженное состояние в пластине от разности влагосодер­жаний при сушке

l₀ - начальная длина пластины; 2х - толщина пластины; U - кри­вая распределения влагосодержа­ния по толщине пластины; ∆U - перепад влагосодержания на рас­сматриваемый момент времени; l_к -конечная длина пластины; ∆l - отрезок на который уменьши­лась пластина с каждой стороны; НП - нейтральные плоскости, в ко­торых сокращение пластины прои­зошло пропорционально изменив­шемуся влагосодержанию

Пусть на какой-то момент сушки перепад влагосодержа­ния составляет в пластине ∆U (см. рис. 4.2). Представим, что пластина состоит из отдельных бесконечно тонких полосок, которые могут сокращаться самостоятельно, то­гда длина каждой полоски, согласно формуле (4.2), дол­жна быть пропорциональна влагосодержанию. Однако пластина целая, и усадка ее заканчивается при конеч­ной длине l_к, соответствующей среднему влагосодержа­нию. Таким образом поверхностные слои пластины сок­ратились до l_к, а должны были бы быть значительно ко­роче, в то время как центральные слои, которые тоже сократились до l_к, должны были быть длиннее. Следо­вательно, поверхностные слои растянуты, а централь­ные— сжаты.

Эти напряжения и обозначены на чертеже знаками «плюс» и «минус». Только два слоя НП (нейтральная плоскость) уменьшились в размерах пропорционально влагосодержанию и напряженное состояние в них отсут­ствует. Возрастающая скорость сушки ведет к увеличе­нию перепада влагосодержания ∆U и, как это следует из рис. 4.2, к усилению напряженного состояния. Развива­ющиеся силы растяжения и сжатия стараются сдвинуть отдельные слои по отношению друг к другу. Возникают тангенциальные напряжения, которые, как только они превысят прочность материала, ведут к образованию тре­щин и разрушению структуры изделия.

В процессе сушки нагрев материала неравномерный, что так же, как и перепад влагосодержаний, приводит к возникновению объемно-напряженного состояния, кото­рое развивается при нагреве из-за перепадов температур на поверхности и в центре материала.

Возвращаясь к рис. 4.1, отметим: перепад температур ∆l=t_п-t_ц наблюдается в первый период сушки и увели­чивается до конца первого периода. Во втором периоде перепад уменьшается и исчезает. Вторично перепад температур возникает в третьем периоде при падающей скорости сушки. Для наглядного представления о напряжен­ном состоянии, возникающем вследствие нагрева, рас­смотрим аналогичную пластину длиной l₀ (рис. 4.3), подвергнутую нагреву в процессе сушки. Для упрощения предположим, что нагревают ее только с двух сторон (од­номерное поле), остальные поверхности пластины теплоизолированы.

В пластине наблюдается перепад температур, кото­рый по мере сушки в первый и третий периоды возраста­ет. Определим на какой-то момент перепад температур в пластине ∆t и нанесем его на рисунок 4.3. Представим, что пластина состоит из отдельных бесконечно тонких поло­сок, которые могут удлиняться и сокращаться самостоя­тельно, тогда длина каждой полоски может быть опре­делена по формуле

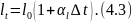
где 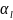- коэффициент линейного расширения.

Рис. 4.3. Напряженное состояние в пластине от разности температур присушке

l₀ - начальная длина пластины; 2х - толщина пластины; ∆t - перепад тем­ператур по толщине пластины в рассматриваемый момент времени; ∆t _п - отрезок, на который должна была удлиниться поверхностная полоска пла­стины; l_t=f(t) - конфигурация, которую должна была принять пластина, со­стоящая из несвязанных полосок; l_п=f(t_ср) - конечная, реальная длина пластины; НП - нейтральные плоскости, в которых удлинение соответствует температуре при сушке

Вычислив длину каждой бесконечно тонкой полоски и отложив половину ее на чертеже пунктиром от середи­ны пластины, получим реальную конфигурацию тела l_t=f(t), которую должна была приобрести пластина при нагревании. Однако общее удлинение пластины выразилось меньшей величиной и длина ее стала равной l_п= f(t_ср).

Таким образом поверхностные слои должны были уд­линиться на ∆t_п, а удлинились меньше и испытывают сжимающие напряжения, а центральные слои удлинились более положенного и испытывают растягивающие напря­жения. Эти напряжения и показаны знаками «плюс» и «минус» на чертеже. На чертеже буквами НП обозначены нейтральные плоскости, в которых напряжения не воз­никли.

Сравнивая напряженные состояния, развивающиеся от разности влагосодержаний (см. рис. 4.2) и от разности температур (см. рис. 4.3), видим, что они имеют проти­воположные знаки. Следовательно, при сложении необхо­димо из большего вычесть меньшее. Так как развиваю­щееся напряженное состояние от разности влагосодержания почти на порядок больше, чем от разности температур, то суммарное напряженное состояние будет несколько меньшим, чем развивающееся от разности влагосодер­жаний. Это напряженное состояние будет действовать на слои пластины, пытаясь сдвинуть один слой относитель­но другого, вызывать таким образом тангенциальные напряжения, которые в случае превышения ими прочно­сти материала приводят к растрескиванию. Когда тан­генциальные напряжения значительно превысят проч­ность материала, наблюдается разрушение материала.

Тепло- и массообмен в процессе сушки. Сушка материалов возможна при любой, даже отри­цательной температуре. Для этого необходимо и доста­точно, чтобы парциальное давление водяных паров на поверхности материала было больше, чем в окружающей среде. На этом положении основывалась применявшаяся ранее естественная сушка материалов. Однако скорость такой сушки невелика и не соответствует современному уровню развития промышленности. Для ускорения сро­ков сушки и сокращения количества воздуха, необходи­мого для ассимиляции влаги, стали применять нагретый воздух или продукты горения топлива, которые называ­ют сушильным агентом. Сушильный агент должен харак­теризоваться следующими параметрами: температура сушильного агента должна быть выше температуры мате­риала, а парциальное давление водяных паров в нем дол­жно быть меньше, чем на поверхности материала.

Поэтому если на материал будет воздействовать су­шильный агент, то он будет отдавать теплоту материалу, а с поверхности материала ассимилировать влагу. Эти явления, как уже говорилось, называют внешним тепло-и массообменом. Процессы передачи теплоты, влаги и воздуха внутри материала называют внутренним тепло-и массообменом.

Внешний тепло- и массообмен при сушке. Суш­ка строительных изделий и материалов обычно ведется при невысоких температурах порядка 100 - 200 °С, при которых доминирует конвективный теплообмен между сушильным агентом и материалом. Поэтому в строитель­ной индустрии применяют конвективные сушильные установки.

При конвективном теплообмене поток теплоты q от сушильного агента к материалу можно определить по формуле

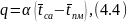
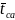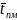где α - коэффициент теплоотдачи от сушильного агента к материалу; - средняя температура сушильного агента в установке; - средняя температура поверхности материала в процессе сушки.

Коэффициент теплоотдачи зависит от аэродинамиче­ских условий обтекания материала сушильным агентом, от свойств сушильного агента, от удельной поверхности материала, с которой происходит испарение, характера движения сушильного агента и целого ряда других фак­торов.

В теплотехнике для описания условий теплоотдачи пользуются системами дифференциальных уравнений, ко­торые в большинстве своем не могут быть решены при­менительно к конкретным условиям. Поэтому конкретные условия теплоотдачи изучают экспериментально, а полученные данные в зависимости от различных переменных факторов обобщают, пользуясь теорией подобия. Для подобных явлений в качестве обязательных закладыва­ют геометрическое подобие, подобие физических струк­тур, начальных состояний и условий поверхностного вза­имодействия тел с окружающей средой. Таким образом, сложный процесс теплоотдачи и массообмена заменяют зависимостью между группой величин, называемых кри­териями подобия. Эти процессы для различных случаев, встречающихся при тепловой обработке строительных изделий, характеризуются основными критериями подобия, приведенными ниже.

В условиях естественной конвекции основным аэроди­намическим критерием является критерий Архимеда (Аr):

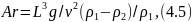
где 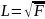- определяющий размер материала; F - поверхность тепло- и массообмена; g-ускорение силы тяжести; ρ₁ и ρ₂ - плотности влажного сушильного агента, соответственно у поверхности материала и в ядре потока; v—коэффициент кинематической вяз­кости.

При вынужденном движении сушильного агента ос­новным аэродинамическим критерием является критерий Рейнольдса (Re):

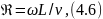
где w — скорость потока теплоносителя; L — определяющий размер —длина поверхности тепло- и массообмена в направлении по­тока сушильного агента; v — коэффициент кинематической вязкости.

Физические свойства влажного газа (сушильного агента) характеризуют термический (Рr) и диффузион­ный (Рr') критерии Прандтля:

где v - коэффициент кинематической вязкости; а - темпера-туропро­водность; D - коэффициент диффузии.

Критерий Фурье (Fo) характеризует связь между ско­ростью изменения температуры и определяющим разме­ром подвергаемых тепловой обработке тел:

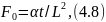
где α - температуропроводность; τ - время; L - определяющий размер.

Связь между теплоотдачей на поверхности тела и пе­редачей теплоты теплопроводностью внутри материала описывается критерием Био (Bi):

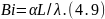
Влияние термодинамических свойств влажного су­шильного агента на интенсивность испарения учитыва­ют критерием Гухмана (Gu):

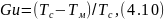
где Т_с и Т_м — абсолютные температуры сушильного агента по су­хому и мокрому термометрам.

Если процесс испарения влаги с поверхности происхо­дит при температуре поверхности, отличной от темпера­туры сушильного агента, а именно такие условия наблю­даются при сушке строительных изделий, то вводят па­раметрический критерий θ:

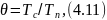
где Т_с — абсолютная температура сушильного агента по сухому тер­мометру; Т_п — абсолютная температура поверхности, с которой происходит испарение.

Подобие температурных полей и парциальных давле­ний на границе материал — сушильный агент определя­ется термическим (Nu) и диффузионным (Nu') критеририями Нуссельта:

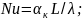
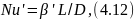
где 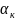- коэффициент конвективного теплообмена; β' — коэффици­ент массообмена; L — определяющий размер материала; λ— тепло­проводность; D — коэффициент диффузии.

Общий вид критериальной зависимости для случая теплообмена, осложненного массообменом, может быть представлен в следующем виде для условий теплообме­на при естественной конвекции:

Nu = f₁(Ar, Рг); (4.13)

для условий теплообмена при вынужденной конвекции:

Nu = f₂(Pe, Рr, Gu, θ); (4.14)

для условий массообмена соответственно при естествен­ной и вынужденной конвекции:

Nu' = f₃ (Ar, Рr') и

Nu'=f₄(Re,Pr',Gu,θ). (4.15)

Экспериментальные исследования позволили устано­вить степенной вид этих функций. Полученные зависи­мости приведены в монографиях и исследованиях, по­священных процессам тепло- и массообмена, и приме­няются для их расчета.

Пользуясь критериями Нуссельта, можно формулу (4.4) определения потока теплоты q для внешнего теп­лообмена переписать в виде

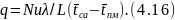
Применительно к конвективному теплообмену сле­дует указать на то, что поток теплоты 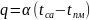, ко­торый получает материал, расходуется на его нагрев, на нагрев находящейся в нем влаги и на испарение влаги с поверхности материала.

В общем расходе теплота, расходуемая на нагрев материала при постоянной ско­рости сушки, значительно меньше, чем затрачиваемая на испарение влаги с поверхности. Влага материала учитывается при его нагреве. Зависимость, представля­ющую балансовое уравнение теплоты для процесса сушки, с некоторым приближением записывают:

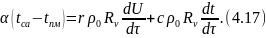
В правой части балансового уравнения первый член 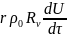учитывает расход теплоты на испарение влаги (уменьшение влагосодержания материала 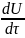), а второй 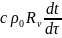учитывает теплоту, затраченную на изменение температуры материала .

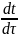Остальные значения в этом уравнении: r — теплота испарения, равная теплоте парообразования и энергии, расходуемой на преодо­ление сил сцепления влаги с поверхностью; ρ₀ — плотность материа­ла; с — удельная теплоемкость материала; R_v—отношение объема материала к его поверхности, с которой происходит испарение.

В процессе сушки величина dU/dτ — отрицательна, поэтому скорость нагрева и скорость сушки при сумми­ровании считают по их абсолютным значениям.

Поток влаги q_m, ассимилирующейся окружающей средой, описывается формулой Дальтона, устанавливающей связь между физическими параметрами, влияющими на ско­рость испарения:

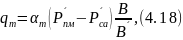
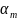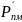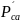где - коэффициент массообмена; - парциальное давление водяных паров на поверхности материала; - парциальное дав­ление водяных паров сушильного агента; В — барометрическое давление при нормальных физических условиях; В' — существую­щее барометрическое давление.

Эта формула в критериальной зависимости может быть представлена в виде

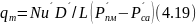
где Nu' - диффузионный критерий Нуссельта; D' - коэффициент диффузии, отнесенный к градиенту парциального давления; L - оп­ределяющий размер; 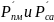- соответственно парциальное дав­ление водяных паров на поверхности материала и в сушильном агенте.

При изотермических условиях между коэффициента­ми диффузии D и D' существует соотношение D=D'R_пТ.

Для пересчета коэффициента диффузии водяных па­ров на любую температуру и давление пользуются формулой

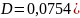
где D — коэффициент диффузии, В и В' указаны в формуле (4.18); R_п —газовая постоянная пара; Т—абсолютная температура воз­душно-паровой смеси.

Формулы (4.14) и (4.18), определяющие взаимодей­ствие влажного материала с сушильным агентом, спра­ведливы для стационарного процесса сушки — периода постоянной скорости сушки. При описании периода па­дающей скорости сушки эти формулы применяют толь­ко для качественного анализа процесса.

Внутренний тепло- и массообмен. Теплота, ко­торую получает поверхность материала при внешнем тепло- и массообмене с𝜌₀R_vdt/dτ (смотреть формулу 4.17), распространяется внутри материала за счет теплопро­водности. Влага при испарении ее с поверхности за счет возникающего градиента влагосодержаний VI/ начина­ет перемещаться по материалу и осложнять распрост­ранение теплоты в материале.

Аналогично обратной задаче - увлажнению при тепло-влажностной обработке - процесс внутреннего теплообмена, осложненный перемещением влаги при сушке, описывается по А. В. Лыкову уравнением

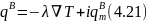
Влага при сушке может перемещаться внутри мате­риала в виде жидкости или пара. Перенос пара, возду­ха и газов, находящихся в материале, про­исходит молекулярным способом за счет диффузии или молярным в результате фильтрации под действием пе­репада общего давления. При удалении влаги в процес­се сушки ее место занимает воздух из окружающей сре­ды. Таким образом, влага и воздух и их движение по материалу взаимосвязаны. Пористость материала в процессе сушки уменьшается, так как частицы материала при удалении влаги сближаются и диаметр пор, и ка­пилляров сокращается.

Поток массы при сушке, как и при тепловлажност­ной обработке, является функцией ряда переменных, однако с достаточной точностью можно пред­ставить его плотность как сумму частных потоков q_mu,q_mt, q_mp.

В общем виде уравнение плотности потока массы будет

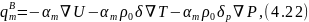
а распространение теплоты в теле

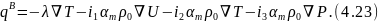
Оба эти уравнения аналогичны справедливы для описания увлажнения при тепло­влажностной обработке бетона, так и для обратного ему процесса — сушки.

Механизм тепло-и массообмена в процессе сушки. Для четкого представле­ния о механизме переноса теплоты и массы проанали­зируем уравнение (4.23) для одномерного пространства. Возьмем неограниченную пластину толщиной 2х из только что сформованного капиллярно-пористого кол­лоидного материала, поме­стим ее в установку с непре­рывно меняющимся сушиль­ным агентом. Через откры­тые поверхности за счет тепло- и массообмена в пластине возникнут перепады влагосодержаний, температур и давлений.I

Рис. 4.4 Характер изменений вла­госодержаний U; температур Т и давлений Р по толщине материала в процессе сушки

I, II, III—периоды сушки; U_ц, T_ц, P_ц, U_п, T_п, P_п—соответственно влагосодержание, температура и давление в центре и на поверхно­сти материала

На рис. 4.4 а, б, в характер изменения влагосодержания U, температур Т и давлений Р на поверхности и в центре пластины в различные периоды сушки. Абсолютные зна­чения влагосодержаний U, температур Т и давлений в зависимости от материалов, их пористости, от режимов сушки могут меняться, однако характер кривых пред­ставляется близким к приведенным на рис. 4.4.

На рис. 4.4, а показано изменение перепада влагосо­держаний ∆U= U_ц—U_п в процессе сушки. В первый (I) период ∆U возрастает. Начиная со второго (II) перио­да ∆U начинает убывать до конца сушки.

На рис. 4.4, б показаны перепады температур ∆Т= Т_п—Т_ц в процессе сушки: сначала и до конца первого периода ∆Т возрастает. Во второй период начинает убывать, и в точке К температуры центра и поверхности одинаковы. Перепад температур вновь возникает в тре­тий период. Сначала он возрастает, но по мере удале­ния влаги из центра перепад температур снова умень­шается.

На рис. 4.4, в показано изменение перепада давлений ∆Р = Р_ц—Р_п также в процессе сушки по периодам. В первый и второй периоды сушки избыточное давление в центре материала возрастает и где-то в точке N, ближе к концу второго периода, начинает падать. Снижение давления объясняется постепенной заменой влаги в по­рах и капиллярах сушильным агентом, у которого бо­лее высокая температура, чем у материала. Проникая в капилляры, он несколько охлаждается, а часть водя­ных паров конденсируется в порах. Давление в пузырь­ках попавшего в капилляры сушильного агента снижа­ется. Это снижение давления в материале до атмосфер­ного, а иногда несколько ниже атмосферного, как показано на рисунке 4.4, в, наблюдается в третий период. Давление на поверхности материала во все периоды равно атмосферному - 0,1 МПа.

Для большей наглядности возьмем чертеж неогра­ниченной пластины (рис. 4.5) и рассмотрим перемеще­ние массы влаги в различные периоды сушки в зависи­мости от изменения ∆U, ∆Т и ∆Р.

На рис. 4.5, а распределение по толщине пластины влагосодержания — кривая U, температур — кривая Т и давлений — кривая Р. Следовательно, значе­ния ∆U, ∆T и ∆Р, взятые по рисунку 4.4, соответствуют ве­личинам ∆U, ∆T и ∆Р по рисунку 4.7. Покажем на рис. 4.5, а направление векторов градиентов U, Т и Р и вы­зываемых ими частных потоков массы, векторов q_mu, q_mt и q_mp. Обозначим для первого периода сушки част­ные потоки, направленные к поверхности и способству­ющие передвижению влаги к поверхности испарения, положительными знаками, а тормозящие передвижение влаги к поверхности испарения — отрицательными. Тог­да основное уравнение плотности потока массы (4.22) может быть для первого периода сушки записано в об­щем виде

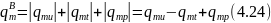
Рис. 4.5. Схема направлений векторов частных потоков массы при сушке а, б, в — соответственно для первого, второго и третьего периодов сушки

На рис. 4.5, б представим неограниченную пластину для второго (II) периода сушки и аналогично постро­им кривые распределения влагосодержания U, темпера­туры Т и давления Р. Также покажем направление век­торов ∇U, ∇T, ∇P И q_mu, q_mt и q_mp.

Рассматривая совместно рис. 4.5, б и 4.4, б отметим, что направление векторов частных потоков массы не изменяется до точки. Однако интенсив­ность потоков q_mu и q_mt падает, а интенсивность потока q_mp возрастает.

Рис. 4.5, б выполнен для второго периода, изменяю­щего характер после точки К. В этом случае необходи­мо отметить, что интенсивность частного потока массы q_mt продолжает снижаться. Частный поток массы силу 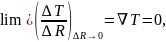, исчезает — q_mt =0. Поэтому он на рис. 4.5, б не показан. Частный поток массы q_mp возрастает до точки N (см. рис. 4.4, в), а потом к концу второго периода уменьшается. Тогда для второго периода сушки основное управление плотности потока массы может быть представлено в общем виде

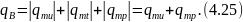
Для третьего (III) периода сушки (рис. 4.5, в) отме­тим следующее. Частный поток массы q_mu продолжает снижаться. Вновь возникает перепад температуры ∇T=T_п—Т_ц, что сопровождается появлением частного по­тока массы q_mt, опять направленного к центру. Проис­ходят изменения и с частным потоком массы q_mp. Сначала его интенсивность резко снижается и в точке L он исчезает. Далее этот частный поток или вообще не воз­никает (если не появляется в материале давление ниже атмосферного), или возникает с очень малой интенсивностью, но с обратным знаком. Все это и представлено на рисунке.

На рис.4.5, в приведен случай, когда внутри мате­риала образуется незначительное отрицательное давле­ние (разрежение). Для этих условий (по рис. 4.5, в) основное управление частного потока массы может быть записано в виде

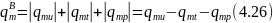
Все это позволяет сделать следующие выводы.

I период, самый короткий и количество испаряемой влаги невелика т.к. влага испаряется исключительно только с поверхности.

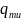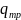II период, передача влаги за счет и , вектора направлены в одну сторону поверхности именно это условие позволяет вести сушку с постоянной скоростью испарения влаги.

III период, резко снижается содержание влаги т.к. уменьшается, одновременно возникают поток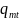и и уже направлены в строну от поверхности.