
- •1. Дробно-рациональная функция
- •2. Показательная функция:
- •3. Тригонометрические функции:
- •4. Гиперболические функции:
- •5. Логарифмическая функция.
- •6. Общая степенная функция:
- •14.4. Понятие аналитической функции. Сопряженные гармонические функции
- •12.1 Особые точки аналитических функций
- •12.2 Вычеты в особых точках
- •12.3 Вычисление вычетов
- •12.4 Основная теорема теории вычетов
- •12.5 Вычисление интегралов вида
12.1 Особые точки аналитических функций
Определение. Точка а называется особой
точкой функции ![]() ,
если в этой точке функция имеет разрыв
или у нее не существует производная.
,
если в этой точке функция имеет разрыв
или у нее не существует производная.
Точка а называется изолированной
особой точкой функции
,
если существует такое ![]() ,
что в кольце
,
что в кольце ![]() функция
аналитична.
функция
аналитична.
В дальнейшем рассматриваются только изолированные особые точки.
Пусть а – изолированная особая точка функции .
Определение
1. Точка а называется устранимой
особой точкой функции
,
если существует конечный предел ![]() .
.
Теорема 1. Для того, чтобы а была устранимой особой точкой функции необходимо и достаточно, чтобы в разложении в кольце в ряд Лорана в нем отсутствовала главная часть.
Если
положить ![]() ,
то особенность исчезает.
,
то особенность исчезает.
Определение
2. Точка а называется полюсом функции
,
если ![]() .
.
Теорема 2. Для того, чтобы а была полюсом функции необходимо и достаточно, чтобы в разложении в кольце в ряд Лорана в главной части было конечное число слагаемых.
Замечание. Если
главная часть начинается с члена,
содержащего ![]() ,
то говорят, что точка а есть полюс n-го
порядка. Если n=1,
то полюс называется простым.
,
то говорят, что точка а есть полюс n-го
порядка. Если n=1,
то полюс называется простым.
Определение
3. Если ![]() не
существует, то точка а называется существенно
особой точкой функции
.
не
существует, то точка а называется существенно
особой точкой функции
.
Теорема 3. Для того, чтобы а была существенно особой точкой функции необходимо и достаточно, чтобы в разложении в кольце в ряд Лорана в главной части было бесконечное число слагаемых.
Ряд
Лорана —
двусторонне бесконечный степенной ряд
по целым степеням ![]() ,
то есть ряд вида
,
то есть ряд вида
![]()
Этот ряд понимается как сумма двух рядов:
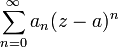 — положительная
часть ряда
Лорана (иногда называется правильной)
и
— положительная
часть ряда
Лорана (иногда называется правильной)
и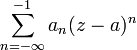 — отрицательная
часть ряда
Лорана (иногда называется главной).
— отрицательная
часть ряда
Лорана (иногда называется главной).
При этом ряд Лорана считается сходящимся тогда и только тогда, когда сходятся его правильная и главная части. Термин назван в честь французского математика
областью сходимости ряда Лорана (60) будет пересечение областей сходимости его частей и имеет место теорема:
функция ![]() аналитическая
в круговом кольце
аналитическая
в круговом кольце ![]() однозначно
представляется в этом кольце сходящимся
рядом Лорана, а коэффициенты определяются
выражением:
однозначно
представляется в этом кольце сходящимся
рядом Лорана, а коэффициенты определяются
выражением:
|
(61) |
где ![]() -
произвольный замкнутый контур,
принадлежащий кольцу
.
Формула (61)
определяет прямой способ разложения
функции
в
ряд Лорана.
-
произвольный замкнутый контур,
принадлежащий кольцу
.
Формула (61)
определяет прямой способ разложения
функции
в
ряд Лорана.
12.2 Вычеты в особых точках
Пусть а – изолированная особая точка функции .
Теорема. Интегралы по всем простым контурам, окружающим особую точку, равны между собой.
Таким образом, интегралы по простым контурам, окружающим особую точку, являются характеристикой точки, а не контура.
Определение. Пусть G - любой простой контур, окружающий особую точку а. Величина

называется вычетом функции
в
точке а и
обозначается символом ![]() .
.
Сравним это выражение с выражением для коэффициентов ряда Лорана функции :
 .
.
Если взять n = – 1, то получим
 ,
,
и
получается, что ![]() .
.
Итак: Вычетом
функции
в
точке а называется
величина  ,
где интеграл берется по любому простому
контуру, окружающему особую точку.
Численно вычет равен коэффициенту
,
где интеграл берется по любому простому
контуру, окружающему особую точку.
Численно вычет равен коэффициенту ![]() в
разложении функции
в
ряд Лорана в окрестности точки а.
в
разложении функции
в
ряд Лорана в окрестности точки а.

